多核编程中的锁竞争难题
多核编程中的锁竞争现象
在前一篇讲解多核编程的几个难题及其对策(难题一)的文章中提到了锁竞争会让串行化随CPU的核数增多而加剧的现象,这篇文章就来对多核编程的锁竞争进行深入的分析。
为了简化起见,我们先看一个简单的情况,假设有4个对等的任务同时启动运行,假设每个任务刚开始时有一个需要锁保护的操作,耗时为1,每个任务其他部分的耗时为25。这几个任务启动运行后的运行情况如下图所示:
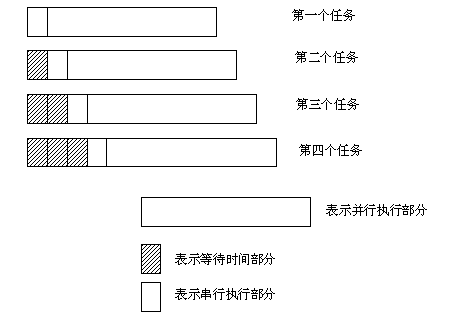
图1:对等任务的锁竞争示意图
在上图中,可以看出第1个任务直接执行到结束,中间没有等待,第2个任务等待了1个时间单位,第3个任务等待了2个时间单位,第3个任务等待了3个时间单位。
这样有3个CPU总计等待了6个时间单位,如果这几个任务是采用OpenMP里的所有任务都在同一点上进行等待到全部任务执行完再向下执行时,那么总的运行时间将和第四个任务一样为29个时间单位,加速系数为:(1+4×25)/ 29 = 3.48
即使以4个任务的平均时间27.5来进行计算,加速系数=101/27.5 = 3.67
按照阿姆尔达定律来计算加速系数的话,上述应用中,串行时间为1,并行处理的总时间转化为串行后为100个时间单位,如果放在4核CPU上运行的话,加速系数=p / (1 + (p-1)*f) = 4/(1+(4-1)*1/101) = 404/104 = 3.88
这就产生了一个奇怪的问题,使用了锁之后,加速系数连阿姆尔达定律计算出来的加速系数都不如,更别说用
Gustafson
定律计算的加速系数了。
其实可以将上面
4
个任务的锁竞争情况推广到更一般的情况,假设有锁保护的串行化时间为
1
,可并行化部分在单核
CPU
上的运行时间为
t
,
CPU
核数为
p
,那么在
p
个对成任务同时运行情况下,锁竞争导致的总等待时间为:
1
+
2
+
…
+
p
=
p*(p-1)/2
耗时最多的一个任务所用时间为:
p + t/p
使用耗时最多的一个任务所用时间来当作并行运行时间的话,加速系数如下
S(p) = (t+1) / (p + t/p) = p*(t+1) / (p*p+t)
(锁竞争下的加速系数公式)
这个公式表明在有锁竞争情况下,如果核数固定情况下,可并行化部分越大,那么加速系数将越大。在并行化时间固定的情况下,如果
CPU
核数越多,那么加速系数将越小。
还是计算几个实际的例子来说明上面公式的效果:
令
t=100, p=4,
加速系数=
4
×(
100 +1)/ (4*4+100) = 3.48
令
t=100, p=16,
加速系数=
16
×(
100+1) / (16*16+100) = 4.54
令
t=100, p=64,
加速系数=
64
×(
100+1) / (64*64+100) = 1.54
令
t=100, p=128,
加速系数=
128
×(
100+1) / (128*128+100) = 0.78
从以上计算可以看出,当核数多到一定的时候,加速系数不仅不增加反而下降,核数增加到
128
时,加速系数只有
0.78
,还不如在单核
CPU
上运行的速度。
上面的例子中,锁保护导致的串行代码是在任务启动时调用的,其实对等任务中在其他地方调用的锁保护的串行代码也是一样的。
对等型任务的锁竞争现象在实际情况中是很常见的,比如服务器软件,通常各个客户端处理任务都是对等的,如果在里面使用了锁的话,那么很容易造成上面说的加速系数随
CPU
核数增多而下降的现象。
以前的服务器软件一般运行在双
CPU
或四
CPU
机器上,所以锁竞争导致的加速系数下降现象不明显,进入多核时代后,随着
CPU
核数的增多,这个问题将变得很严重,所以多核时代对程序设计提出了新的挑战。以前的多任务下的编程思想放到多核编程上不一定行得通。
所以简单地认为多核编程和以前的多任务编程或并行计算等同的话是不切实际的,在讲串行化难题的那篇文章中提出了一些解决方面的对策,但是那些对策还有待业界继续努力才能做得到。
当然由于目前市面上销售的多核CPU还是双核和四核的,等到16核以上的CPU大规模进入市场可能还有几年时间,相信业界在未来的几年内能够对于上面对等任务上的锁竞争问题找到更好的解决方案。
作者介绍:
周伟明,自由职业,从事软件行业十年有余。目前主要关注软件测试、多核编程、软件设计等基础方面的内容。写有《多任务下的数据结构与算法》一书,目前正在写作《软件测试实践》一书,计划在不久的将来写一本多核编程方面的书籍。
Trackback: http://tb.blog.csdn.net/TrackBack.aspx?PostId=1559718