实时绘制基于LOD的地形相关技术
LOD(levels of etails细节层次)是解决大规模地形实时渲染的一项关键技术。在地形中实现LOD技术后大大加速了地形的渲染。其基本思想是:对地形生成具有不同层次(不同分辨率)的多个版本,在绘制地形时依据视点来选择合适的层次细节进行绘制。本文用基于四叉树构建的地形来实现相关Lod算法,有关四叉树构建地形的技术可参考“引擎技术研究之地形技术”。


可把全部叶子节点保存在数组Leaf,查找邻接节点时可遍历Leaf获取,可根据以下条件判断四个邻接节点:
下[2]=当[0] && 下[3]=当[1]
右[0]=当[1] && 右[2]=当[3]
上[0]=当[2] && 上[1]=当[3]
左[3]=当[2] && 左[1]=当[0]
2根据视点选择层次细节
先计算每个叶子节点与摄像机视点的距离distance,为每个节点设计一属性Unit作为分辨率,依据distance设置Unit值,如:
if (title->distance<50.0) { title->unit=1; }
else if (title->distance<100) { title->unit=2; }
else if (title->distance<200) { title->unit=4; }
Unit值适宜设置为2的n次幂(1 ,2 ,4 ,8, 16 …….),如图所示:

3构造节点的三角形
首先确定当前节点是叶子节点title,再根据叶子节点的ditance设置其Unit值,每行的索引数(像素)为MESH_WIDTH+1,节点里每行或每列的网格数corner[1]-corner[0],用n[4]保存每个块的四个顶点索引值。
有两种构造情况,一是有某一邻接节点与当前节点的Unit不等时,二是四个邻接点的Unit均与当前节点相同。
A
先处理第一种情况,若Unit=1则一个网格作为一个块构造两三角形,Unit=2,则2x2个网格作为一个块构造两个三角形,以此类推。实现如下:
for(int j=0;j<wide;j+=title->unit)
{
for(int i=0;i<wide;i+=title->unit) //遍历每个块
{
n[0]=title->corner[0]+j*numrow+i;//设置块四个顶点索引值
n[1]=n[0]+title->unit;
n[2]=n[0]+numrow*title->unit;
n[3]=n[2]+title->unit;
index[m_NumIndex++]=n[0];
index[m_NumIndex++]=n[2];
index[m_NumIndex++]=n[1];//左下三角形
index[m_NumIndex++]=n[1];
index[m_NumIndex++]=n[2];
index[m_NumIndex++]=n[3];//右上三角形
}
}
index为指向索引缓冲区内存的指针,m_NumIndex为索引数量,以上可完成块的三角形构造。
B现处理第二种情况。块的三角形分两部分构造,一是正常的,下图黑色三角形。
二是交界处需特殊构造的三角形,如下图红色线条三角形:

(1)现画正常的三角形,遍历每个块:
for(int j=0;j<wide;j+=title->unit)
{
for(int i=0;i<wide;i+=title->unit) //遍历每个块
{
n[0]=title->corner[0]+j*numrow+i;//设置块四个顶点索引值
n[1]=n[0]+title->unit;
n[2]=n[0]+numrow*title->unit;
n[3]=n[2]+title->unit;
先处理上边界:
if ((title->neigbour[2]!=NULL&&title->neigbour[2]->unit>title->unit)
&&(j<wide&&j>=wide-title->unit&&(i/title->unit)%2==1)) //处理序号为单数的块
{
if (!((title->neigbour[1]!=NULL)&&(title->unit<title->neigbour[1]->unit)
&&(i>=(wide-title->unit))&&(j>=(wide-title->unit))))
{ //若上邻接点和右邻接点Unit均大于当前Unit,则不构造如图所示红色三角形
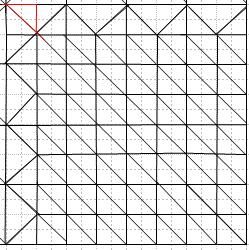
index[m_NumIndex++]=n[0]; //画块里右下三角形
index[m_NumIndex++]=n[3];
index[m_NumIndex++]=n[1];
}
}
else if ((title->neigbour[2]!=NULL&&title->neigbour[2]->unit>title->unit)
&& (j<wide&&j>=wide-title->unit&&(i/title->unit)%2==0)) //处理序号为双的块
{
if (!((title->neigbour[3]!=NULL)&&(title->unit<title->neigbour[3]->unit)
&&(i<=title->unit)&&(j>=(wide-title->unit))))
{ //若上邻接点和左邻接点Unit均大于当前Unit,则不构造如图所示红色三角形
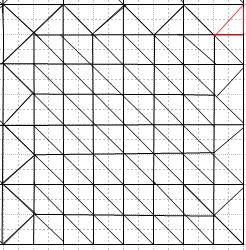
index[m_NumIndex++]=n[0];// 画块里左下三角形
index[m_NumIndex++]=n[2];
index[m_NumIndex++]=n[1];
}
}
else 处理下边界
else 处理左边界
else 处理右边界
else 一般构造
{
index[m_NumIndex++]=n[0];
index[m_NumIndex++]=n[2];
index[m_NumIndex++]=n[1];
index[m_NumIndex++]=n[1];
index[m_NumIndex++]=n[2];
index[m_NumIndex++]=n[3];
}
}//结束正常构造
(2)构造节点交界处三角形
处理上边界:
if (title->neigbour[2]!=NULL&&title->neigbour[2]->unit>title->unit)
{ //上邻接点Unit大于当前节点
for (int k=0;k<wide;k=k+2*title->unit)
{
n[0]=title->corner[2]+k;
n[2]=n[0]+2*title->unit;
n[1]=(n[0]+n[2])/2-numrow*title->unit;
index[m_NumIndex++]=n[0];
index[m_NumIndex++]=n[2];
index[m_NumIndex++]=n[1];
}
}
处理下边界。。。
处理左边界。。。
处理右边界。。。
最终实现LOD的地形构造效果图
