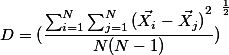层次聚类算法BIRCH(另附Java版下载地址)
BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies)天生就是为处理超大规模(至少要让你的内存容不下)的数据集而设计的,它可以在任何给定的内存下运行。关于BIRCH的更多特点先不介绍,我先讲一下算法的完整实现细节,对算法的实现过程搞清楚后再去看别人对该算法的评价才会感受深刻。
你不需要具备B树的相关知识,我接下来会讲得很清楚。
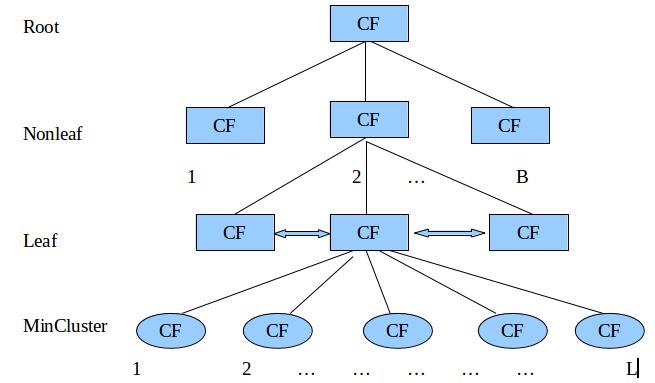
BIRCH算法的过程就是要把待分类的数据插入一棵树中,并且原始数据都在叶子节点上。这棵树看起来是这个样子:
在这棵树中有3种类型的节点:Nonleaf、Leaf、MinCluster,Root可能是一种Nonleaf,也可能是一种Leaf。所有的Leaf放入一个双向链表中。每一个节点都包含一个CF值,CF是一个三元组![]() ,其中data point instance的个数,
,其中data point instance的个数,![]() 和
和![]() 是与数据点同维度的向量,
是与数据点同维度的向量,![]() 是线性和,
是线性和,![]() 是平方和。比如有一个MinCluster里包含3个数据点(1,2,3),(4,5,6),(7,8,9),则
是平方和。比如有一个MinCluster里包含3个数据点(1,2,3),(4,5,6),(7,8,9),则
N=3,
![]() =(1+4+7,2+5+8,3+6+9)=(12,15,18),
=(1+4+7,2+5+8,3+6+9)=(12,15,18),
![]() =(1+16+49,4+25+64,9+36+81)。
=(1+16+49,4+25+64,9+36+81)。
就拿这个MinCluster为例,我们可以计算它的
我们还可以计算两个簇之间的距离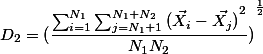 ,当然你也可以使用D0,D1,D3等等,不过在这里我们使用D2。
,当然你也可以使用D0,D1,D3等等,不过在这里我们使用D2。
有意思的是簇中心、簇半径、簇直径以及两簇之间的距离D0到D3都可以由CF来计算,比如
簇间距离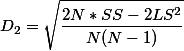 ,这里的N,LS和SS是指两簇合并后大簇的N,LS和SS。所谓两簇合并只需要两个对应的CF相加那可
,这里的N,LS和SS是指两簇合并后大簇的N,LS和SS。所谓两簇合并只需要两个对应的CF相加那可
CF1 + CF2 = (N1 + N2 , LS1 + LS2, SS1 + SS2)
每个节点的CF值就是其所有孩子节点CF值之和,以每个节点为根节点的子树都可以看成 是一个簇。
Nonleaf、Leaf、MinCluster都是有大小限制的,Nonleaf的孩子节点不能超过B个,Leaf最多只能有L个MinCluster,而一个MinCluster的直径不能超过T。
算法起初,我们扫描数据库,拿到第一个data point instance--(1,2,3),我们创建一个空的Leaf和MinCluster,把点(1,2,3)的id值放入Mincluster,更新MinCluster的CF值为(1,(1,2,3),(1,4,9)),把MinCluster作为Leaf的一个孩子,更新Leaf的CF值为(1,(1,2,3),(1,4,9))。实际上只要往树中放入一个CF(这里我们用CF作为Nonleaf、Leaf、MinCluster的统称),就要更新从Root到该叶子节点的路径上所有节点的CF值。
当又有一个数据点要插入树中时,把这个点封装为一个MinCluster(这样它就有了一个CF值),把新到的数据点记为CF_new,我们拿到树的根节点的各个孩子节点的CF值,根据D2来找到CF_new与哪个节点最近,就把CF_new加入那个子树上面去。这是一个递归的过程。递归的终止点是要把CF_new加入到一个MinCluster中,如果加入之后MinCluster的直径没有超过T,则直接加入,否则譔CF_new要单独作为一个簇,成为MinCluster的兄弟结点。插入之后注意更新该节点及其所有祖先节点的CF值。
插入新节点后,可能有些节点的孩子数大于了B(或L),此时该节点要分裂。对于Leaf,它现在有L+1个MinCluster,我们要新创建一个Leaf,使它作为原Leaf的兄弟结点,同时注意每新创建一个Leaf都要把它插入到双向链表中。L+1个MinCluster要分到这两个Leaf中,怎么分呢?找出这L+1个MinCluster中距离最远的两个Cluster(根据D2),剩下的Cluster看离哪个近就跟谁站在一起。分好后更新两个Leaf的CF值,其祖先节点的CF值没有变化,不需要更新。这可能导致祖先节点的递归分裂,因为Leaf分裂后恰好其父节点的孩子数超过了B。Nonleaf的分裂方法与Leaf的相似,只不过产生新的Nonleaf后不需要把它放入一个双向链表中。如果是树的根节点要分裂,则树的高度加1。
最后我们来总结一BIRCH的优势和劣势。
优点:
- 节省内在。叶子节点放在磁盘分区上,非叶子节点仅仅是存储了一个CF值,外加指向父节点和孩子节点的指针。
- 快。合并两个两簇只需要两个CF算术相加即可;计算两个簇的距离只需要用到(N,LS,SS)这三个值足矣。
- 一遍扫描数据库即可建立B树。
- 可识别噪声点。建立好B树后把那些包含数据点少的MinCluster当作outlier。
- 由于B树是高度平衡的,所以在树上进行插入或查找操作很快。
缺点:
- 结果依赖于数据点的插入顺序。本属于同一个簇的点可能由于插入顺序相差很远而分到不同的簇中,即使同一个点在不同的时刻被插入,也会被分到不同的簇中。
- 对非球状的簇聚类效果不好。这取决于簇直径和簇间距离的计算方法。
- 对高维数据聚类效果不好。
- 由于每个节点只能包含一定数目的子节点,最后得出来的簇可能和自然簇相差很大。
- BIRCH适合于处理需要数十上百小时聚类的数据,但在整个过程中算法一旦中断,一切必须从头再来。
- 局部性也导致了BIRCH的聚类效果欠佳。当一个新点要插入B树时,它只跟很少一部分簇进行了相似性(通过计算簇间距离)比较,高的efficient导致低的effective。
原文来自:博客园(华夏35度)
另附一个老外用Java实现的BIRCH算法下载地址:
http://www.perdisci.com/projects/jbirch