Predicting numeric values: Regression 笔记

Predicting numeric values: Regression (预测数值型数据: 回归) 属于监督学习算法, 它可以对连续型的数据进行分类 .

优点	结果易于理解, 计算上不复杂
缺点	对非线性的数据拟合不好
适用数据类型	数值型, 标称型

基础概念
1. 线性回归, 指可以将输入项分别乘以一些常量, 再将结果加起来得到输出. 
2. 最小二乘法, 确保预测y值与真实y值之间的差值的平方和最小.

算法描述
1. 标准线性回归
本文采用的是最小二乘法, 通过数学公式推导, 可直接由公式矩阵运算求出回归系数. 
 
以上结果推导过程如下: (公式输入太麻烦, 直接从Wiki截图了)
(1). 问题描述 (点小图看大图)
(2). 推导过程 (点小图看大图)

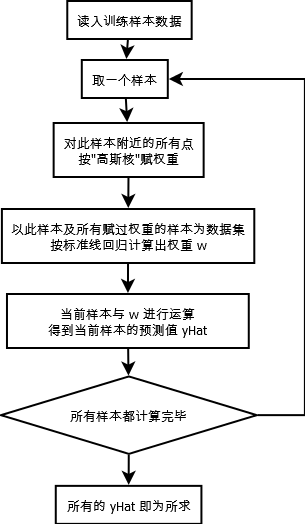
2. 局部加权线性回归(Locally Weighted Liner Regression, LWLR) 
(1). 对训练集中的每个点 testPoint, 都对它附近的所有点赋权重 (代码 67-69 行)
(2). 本文 LWLR 采用"高斯核"进行赋权重, 高斯核对应权重为: (代码 69 行)

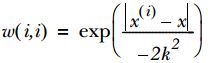
(3). 随着训练样本与测试数据点 testPoint 距离的增加, 权重将以指数级速度递减, 通过参数 k 控制递减速度
(4). 对每个 testPoint 及其周围赋过权重的其他点进行标准线性回归, 求出其对应权重
(5). 对于(4)中求出的权重, 与 testPoint 进行运算, 所求出的点 yHat, 即为预测点 (代码 79, 88 行)

算法流程图
1. 标准线性回归
 数学公式推导计算, 无流程图.

2. 局部加权线性回归

代码

# -*- coding: utf-8 -* 
from numpy import *

# 读入数据, 返回两个集合, 一个包含除最后一列外的数据, 一个只包含最后一列
# 前两列是点的 X, Y坐标, 最后一列是数据所属标签(label)
def loadDataSet(fileName):      
    # 获取列数
    numFeat = len(open(fileName).readline().split('\t')) - 1 

    # 逐行读取
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))

        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))    # -1 表示最后一列
    return dataMat,labelMat


# 标准回归函数, 按公式计算, 这里没法打公式...
def standRegres(xArr, yArr):
    xMat = mat(xArr); yMat = mat(yArr).T

    # 判断行列式是否为 0, 若为0, 则矩阵不可逆
    xTx = xMat.T*xMat
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return

    # .I 表示求逆
    ws = xTx.I * (xMat.T*yMat)
    return ws


# 图形化显示标准线性回归结果, 包括数据集及它的最佳拟合直线
def standPlot(xArr, yArr, ws):
    import matplotlib.pyplot as plt
    xMat = mat(xArr)
    yMat = mat(yArr)
    yHat = xMat * ws
    # 画点
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xMat[:, 1].flatten().A[0], yMat.T[:, 0].flatten().A[0])
    # 画线, 为了保证直线上的点是按顺序排列, 需先升序排序
    xCopy = xMat.copy()
    xCopy.sort(0)
    yHat = xCopy*ws
    ax.plot(xCopy[:, 1], yHat)
    plt.show()


# 局部加权线性回归
# 1. testPoint 是一个测试数据点, 本函数以每个点为中心计算其他样本的权重(故为局部加权)
# 2. 随着训练样本与测试数据点 testPoint 距离的增加, 权重将以指数级速度递减
#    通过参数 k 控制递减速度
def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]

    # 创建对角权重矩阵, 计算并存放每个样本点的权重
    weights = mat(eye((m)))
    for j in range(m):                      
        diffMat = testPoint - xMat[j,:]     
        weights[j,j] = exp(diffMat * diffMat.T / (-2.0*k**2))
   
    # 判断行列式是否为 0, 若为0, 则矩阵不可逆
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return

    # .I 表示求逆
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws


# 局部加权线性回归测试
# 遍历所有的数据点(行), 对每个点应用 lwlr
def lwlrTest(testArr,xArr,yArr,k=1.0):  
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat


# 图形化显示局部加权线性回归结果, 包括数据集及它的最佳拟合直线
def lwlrPlot(xArr, yArr, yHat):
    import matplotlib.pyplot as plt
    xMat = mat(xArr)
    srtInd = xMat[:, 1].argsort(0)
    xSort = xMat[srtInd][:, 0, :]
    # 画线
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(xSort[:, 1], yHat[srtInd])
    # 画点
    ax.scatter(xMat[:, 1].flatten().A[0], 
               mat(yArr).T[:, 0].flatten().A[0], 
               s=2, c='red')
    plt.show()

    
if __name__ == "__main__":
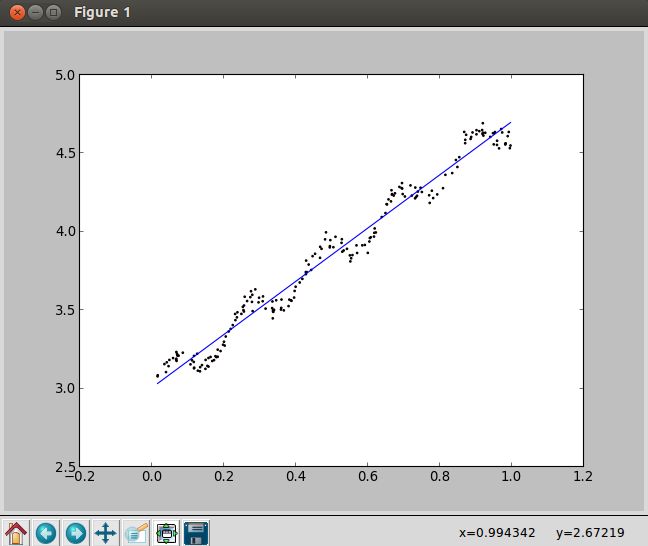
    # 1. 线性回归测试
    xArr, yArr = loadDataSet('ex0.txt')
    ws = standRegres(xArr, yArr)

    # 计算 预测值yHat 与 实际值yMat 的相关系数
    yHat = mat(xArr)*ws
    yMat = mat(yArr)
    print corrcoef(yHat.T, yMat)

    standPlot(xArr, yArr, ws)


    ################################################
    # 2. 局部加权线性回归测试
    # xArr, yArr = loadDataSet('ex0.txt')

    # # 以下 3 个语句应互斥打开
    # # yHat 表示按当前回归函数下得到的预测值
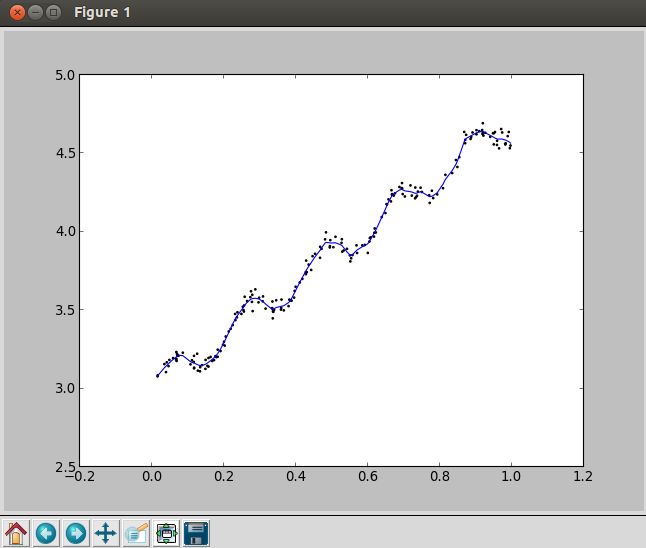
    # # yHat = lwlrTest(xArr, xArr, yArr, 1.0)
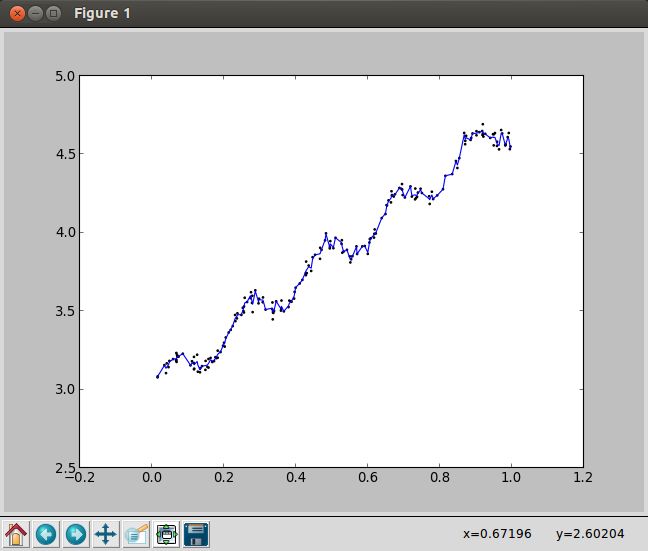
    # # yHat = lwlrTest(xArr, xArr, yArr, 0.01)
    # yHat = lwlrTest(xArr, xArr, yArr, 0.003)

    # lwlrPlot(xArr, yArr, yHat)

 

运行结果
1. 标准线性回归

2. 局部加权线性回归(k=1.0)

3. 局部加权线性回归(k=0.01)

4. 局部加权线性回归(k=0.003)

待补充
1. 岭回归
2. 前向逐步回归
3. 权衡偏差与方差

说明
本文为《Machine Leaning in Action》第八章(Predicting numeric values: Regression)读书笔记, 代码稍作修改及注释. 

好文参考
1.《机器学习入门：线性回归及梯度下降》
2.《线性回归之——最小二乘法》