Python 寻找相近的用户
今天看了一篇文章写的挺好的,所以自己总结一下,发出来大家一起学习一下
欧几里德距离(百度来的哦):欧几里得度量(euclidean metric)(也称欧式距离)是一个通常采用的距离定义,指在m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离),在二维和三维空间中的欧氏距离就是两点之间的实际距离。
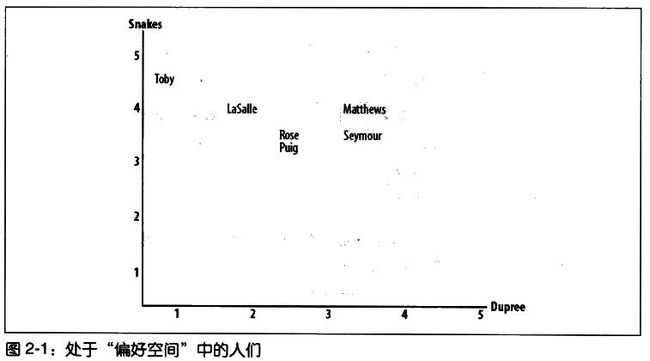
计算相似度评价值的一个非常简单的方法就是欧几里德距离评估法,它以经过人们一致评价的物品作为坐标轴,然后将参与评价的人绘制在图上,并考察他们彼此的距离,如下图所示
该图显示了人员的分布情况,Toby在Snakes轴上和Dupree轴上坐标值为:4.5,1.0,在图中两人距离越近,他们兴趣偏好就约相近。
为了计算图上Toby和LaSalle之间的距离,我们计算出每一轴向上得差值,穷平方后再相加,最后对总和取平方根。
在python中可以使用pow(n,2)对某数求平方,并使用sqrt函数求平方根:
>>> from math import sqrt >>> sqrt(pow(4.5-4,2)+pow(1-2,2)) 1.118033988749895
上述代码可以计算出距离值,偏好越相近的人,距离就越短。不过,我们还需要一个函数,来对偏好越相近的情况给出最大的值,为此,我们可以将函数值加1(这样避免遇到被零整除的错误),并取其倒数:
>>> 1/(1+sqrt(pow(4.5-4,2)+pow(1-2,2))) 0.4721359549995794
这个数字的值总是在0和1 之间,返回1则表示两人具有相同的爱好,下面的代码是计算相似度的函数。
from math import sqrt
#先定义一个字典,里面是用户的评价
critics = {
'Lisa Rose': {'Lady in the Water':2.5, 'Snakes on a Plane':3.5, 'Just My Luck':3.0, 'Superman Returns':3.5,'You, Me and Dupree':2.5, 'The Night Listener':3.0},
'Gene Seymour': {'Lady in the Water':3.0, 'Snakes on a Plane':3.5, 'Just My Luck':1.5, 'Superman Returns':5.0,'You, Me and Dupree':3.0, 'The Night Listener':3.5},
'Michael phillips': {'Lady in the Water':2.5, 'Snakes on a Plane':3.0, 'Superman Returns':3.5,'The Night Listener':4.0},
'Claudia Puig': {'Snakes on a Plane':3.5, 'Just My Luck':3.0, 'Superman Returns':4.0,'The Night Listener':4.5,'You, Me and Dupree':2.5},
'Toby': {'Snakes on a Plane':4.5, 'Superman Returns':4.0,'You, Me and Dupree':1.0}
}
#本函数来计算用户相似度
def sim_distance(prefs,preson1,preson2):
#得到shared_items的列表
si = {}
for item in prefs[preson1]:
if item in prefs[preson2]:
si[item]=1
#无相似度返回0
if len(si) == 0: return 0
#求平方和
sum_of_squares = sum([pow(prefs[preson1] [item]-prefs[person2] [item],2)
for itme in prefs[preson1] if item in prefs[preson2]])
print sum_of_squares
return 1/(1+sqrt(sum_of_squares))