12步解N-S方程之第二步
12步解N-S方程之第二步
# -*- coding: utf-8 -*-
#This is step 2 of python cfd courses.
#Text and code provided under a Creative Commons Attribution license, CC-BY
#. (c) Lorena A. Barba, 2013. Thanks: Gilbert Forsyth for help writing the
#notebooks. NSF for support via CAREER award #1149784.
#
# date author description
# 2014/08/31 wubin 1-d nonlinear convection
#
# pu/pt+u*pu/px=0
# only coef is diff from step1,c is u now,so it is not linear any more.
#
import numpy as np
import matplotlib.pyplot as plt
import time,sys #load some system utilities
from IPython.core.display import clear_output #used for inline animation
#
#gridgen part
nx=41
dx=2.0/(nx-1)
nt=25 #total timesteps,like iterations
dt=0.025 #
c=1.0 #assume wavespeed is 1.0
#
#initialize part
#give every nx vertex a initial value
u=np.ones(nx)
u[0.5/dx:1.0/dx+1]=2 #slice only 1.0/dx,but not 1.0/dx+1
#print u
#
#plt.figure()
#plt.plot(np.linspace(0,2,nx),u)
#plt.show()
u0=np.empty_like(u)
u0=u.copy()
#
#iteration part
un=np.ones(nx) #un is a temporary array
#python's array begins from 0,but why not slice the first element?because in
#iteration ,there is a Ui-1,0-1 is -1,will out of a array bounds.
for n in range(nt):
un=u.copy() #copy the intial values from u to un
for i in range(1,nx):
u[i]=un[i]-un[i]*dt/dx*(un[i]-un[i-1])
plt.figure()
xc=np.linspace(0,2,nx)
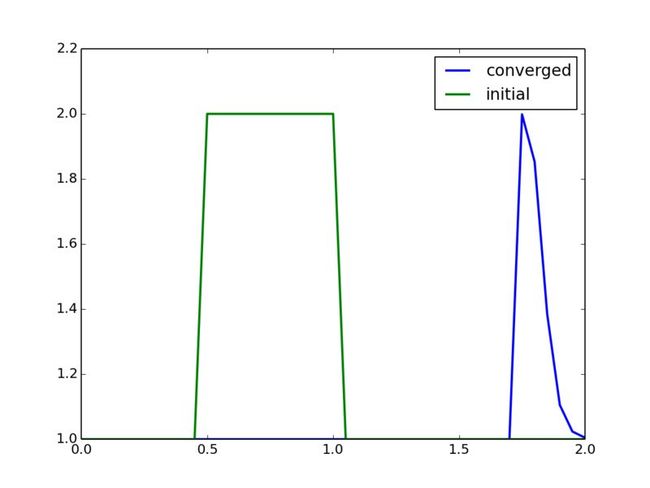
plt.plot(xc,u,linewidth=2.0,label="converged")
plt.plot(xc,u0,linewidth=2.0,label="initial")
plt.legend(loc='upper right')
plt.savefig("F:\PYTHON\python_cfd\step2_comparision.png",dpi=150)
plt.show()
##
##additional question:
#truncation error:截断误差
#what is the truncation error and convergence and other detail?
与第一讲中结果不同的是,一维非线性对流方程似乎有激波的效果在里面(阶梯间断)。