概率图论PGM的D-Separation(D分离)
本文大部分来自:http://www.zhujun.me/d-separation-separation-d.html
其中找了一些资料发现原文中阻塞(block)中(b)部分有出路,黑体部分修改了一下,那么‘四应用例子’部分答案也跟着修改,如果理解有误希望能给予解释,谢谢!资料参考在最下部分‘六、补充参考资料例子’。
一、引言
在贝叶斯网络的学习过程中,经常会遇到(D-Separation)D-分离这个概念,D-分离是寻找网络节点之间的条件独立性的一种方法或者说一种问题的简化处理的技巧。采用D-分离技术,在用贝叶斯网络进行预测,诊断推理等方面,可以提高计算速度,减少计算复杂性。
D-Separation是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法,D-Separation更加直观,且计算简单。对于一个DAG(有向无环图)E,D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。
二、三种情况分析
首先可以看看以下三种简单情况下条件独立的情况(对应于PRML中8.2.1的Three example graphs):
Example One:tail-to-tail (节点C连接的是两个箭头的尾部,如图)
可知, P(a,b,c)=P(a|c)*P(b|c)*P(c) (1)
现在我们求 P(a,b),如果 P(a,b)=P(a)*P(b),则a和b是在c条件下独立分布的。分两种情况进行讨论:
(1)C值不作为观察点。令(1)式对c求积分,消去c值,考虑c是离散的情况,可得
可以看到,与 P(a,b)=P(a)*P(b)不等,所以a和b不是c条件独立的。
(2)C值作为观察点(即以C作为条件)。则可以知道C取某个c状态的概率为 P( c ),c 条件下 a 和 b发生的概率为
P( a,b|c )。 由下式:
可得a 和 b 是 c 条件下独立的。
Example Two:head-to-tail
可知,p(a,b,c)=p(a)*p(c|a)*p(b|c) (2)
同样分两种情况进行讨论:
(1)、c值不作为观察点。对(2)式(考虑c是离散的情况)积分可得:
(2)、c值作为观察点。则图模型表示为:
c 条件下 a 和 b发生的概率为 P( a,b|c )。 由下式:
可知,a 和 b 是 c 条件下独立的。
Example Three:head-to-head
可知 p(a,b,c)=p(a)*p(b)*p(c|a,b) (3)
同理,分两种情况讨论:
(1)、c值不作为观察点。由于所有p(c|a,b)相加和=1,所以有(3)式消去c,可得 p(a,b)=p(a)*p(b),即a与b是条件独立的。
(2)、c值作为观察点。
所以有:
最后不能因式分解成p(a)*p(b)的形式,所以a与b不是c条件独立的。
三、总结
对于较为复杂的 DAG 图,我们可以给出一个普遍意义上的结论 ,也就是 D-Seperation。 对于 DAG 图 E,如果A,B,C是三个集合(可以是单独的节点或者是节点的集合),为了判断 A 和 B 是否是 C 条件独立的, 我们考虑 E 中所有 A 和 B 之间的 无向路径 。对于其中的一条路径,如果她满足以下两个条件中的任意一条,则称这条路径是 阻塞(block) 的:
(a)路径中存在某个节点 X 是 head-to-tial 或者 tail-to-tail 节点(Example one/two),并且 X 是包含在 C 中的;
(b)路径中存在某个节点 X 是 head-to-head 节点(Example Three),并且 X 或 X 的儿子是不包含在 C 中的;
如果 A,B 间所有的路径都是阻塞的,那么 A,B 就是关于 C 条件独立的;否则, A,B 不是关于 C 条件独立的。
四、应用例子
根据D-Seperation分隔定理,我们可以很容易的判断是否是条件独立的。我们来看一个例子:
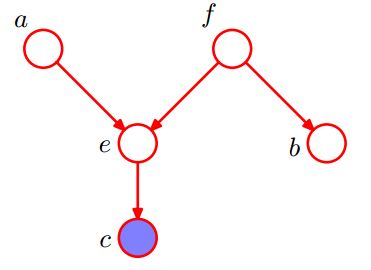
判断图中a与b是否在c条件下独立?a与b是否在f条件下独立?
判断 a 和 b 是否是 c下条件独立的: a 到 b 只有一条路径 a->e->f->b 。 考虑路径上的点 e 和 f :其中e 是 head-to-head 类型的,且 e 的儿子节点就是 c ,根据(b),e不阻断。而节点f是tail-to-tail类型节点,根据(a),f不在c中,所以也有a,b不是c条件下独立。
判断 a 和 b 是否是 f 下条件独立的:路径 a->e->f->b 上的所有节点。考虑路径上的点e和f:节点 e 是head-to-head 类型的,e 和她的儿子节点 c 都不在 f 中,所以(b),e是阻断路径的节点。节点 f 是tail-to-tail类型节点,且 f 节点就在 f中,所以 f 节点阻断了路径。 结论:a 和 b是 f 下条件独立的。
D-Seperation 还可以用来证明独立同分布和马尔科夫边界等。
五、参考资料
1、http://www.andrew.cmu.edu/user/scheines/tutor/d-sep.html#d-sepapplet2
2、http://blog.sina.com.cn/s/blog_7a24649f0101hjdx.html
3、《pattern recognition and meaching learning》-chapter 8:Graphical Model-8.2 conditional independence
六、补充参考资料例子
1.P( G , L | B ),因为根据规则1,给定B阻塞了G和L之间的惟一的路径。根据给定B,M也阻
塞了这个路径,因为M不是证据集的一个成员。
2.I(G,L)和I(B,L),因为按规则,给定空的证据集合, M阻塞了G和L之间、B和L之间的
(惟一)路径(M不是空的证据集的一个成员)。
然而,注意, B和L不是条件独立于给定的M的。因为虽然M在B和L的路径上,但这个路径上的两条弧都指向M,且M在证据集合中—因此在这种情况下,M没有阻塞路径。
七、Cousera上的PGM例子
课上的explanation:
d-sep (D, J | L, I) is the only statement that is true. If we observe L, the V-structure at G is activated, so influence can flow from D through I to J. Likewise, if we observe H, then the V-structure at H is activated, allowing influence to flow from D to J through H.
我的理解:
A.d-seq(D,I|L):考虑路径:Diffuculty-Grage-Intelligence,Grade是head-to-head节点类型,其孩子节点Letter是条件集合中,因此不是条件独立,该项不是d分离。
B.d-seq(D,J|L):考虑路径:Diffuculty-Grage-Letter-Job,节点Grade是head-to-tail节点类型,其不在条件集合中,因此不是条件独立,该项不是d分离。
C.d-seq(D,J|L,I):考虑路径1:Diffuculty-Grage-Letter-Job,L是head-to-tail节点类型,且在条件集合中,因此是条件独立。考虑路径2:Difficulty-Grade-Happy-Job,Happy是head-to-head节点类型,但Happy不在条件集合中,因此条件独立。考虑路径3:Difficulty-Grade-Intelligence-SAT-Job,Grade是head-to-heat节点类型,但不在条件集合中,是条件独立。所有路径都是阻塞,因此该项符合d分离。
D.d-seq(D,J|L,H,I):考虑路径:Diffuculty-Grade-Happy-Job,其中第二条路径,Happy是head-to-head节点类型,但Happy在条件集合中,所以该路径中的D、J不是条件独立,所以该项不是d分离。
一个简单的数学证明:
P(D,S)=P(D)*P(S)