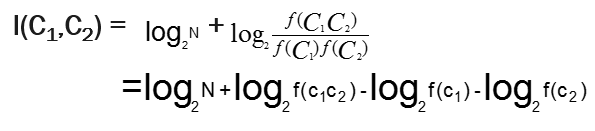搜索引擎之未登录词(Out Of Vocabulary)识别问题
有人问道:南京市长叫江大桥?
你怎么知道的?
因为看到一个标语——南京市长江大桥欢迎您。
未登录词识别问题也叫做:命名实体识别(Named Entity Recognition)
常见的未登录词包括:
人名:张三、陈方安生
地名:安湖路、龙腾苑四区
机构名:泰康人寿、欧姆龙公司
译名:安德森
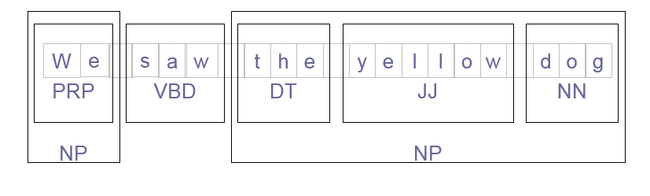
组块识别(Chunking)
切分和标注多个词的单元
每个大的单元叫做组块(chunk)
用模式识别未登录词
例如“高东镇高东二路”,需要把“高东二路”这样不在词典中的路名识别出来。可以先把输入串抽象成待识别的标注序列,然后根据词类识别。例如:
利用模式来识别未登录街道名,识别规则可以表示成如下的形式:
镇后缀 未登录街道 =>镇后缀 UNKNOW 号码 街后缀
识别规则(Product)
lhs = new ArrayList<AddressSpan>(); //左边的模式 rhs = new ArrayList<AddressType>(); //右边的模式 //镇后缀 UNKNOW 号码 街后缀 rhs.add(AddressType.SuffixTown); rhs.add(AddressType.Unknow); rhs.add(AddressType.No); rhs.add(AddressType.SuffixStreet); //镇后缀 未登录街道 lhs.add(new AddressSpan(1,AddressType.SuffixTown));//归约长度是1 //把“UNKNOW 号码 街后缀”3个符号替换成“未登录街道”,因此归约长度是3 lhs.add(new AddressSpan(3,AddressType.Street)); //把规则加到文法库 addProduct(rhs, lhs);
模式文法(Pattern Grammar)
文法(Grammar)是规则的集合,规则的形式:
leftPattern => rightPattern
模式(Pattern)
描述单词的行为
用类型序列来描述模式:SuffixTown Street
词汇化(lexical)的模式:V for n: 动词后接‘for’然后接一个名词
模式文法识别未登录词
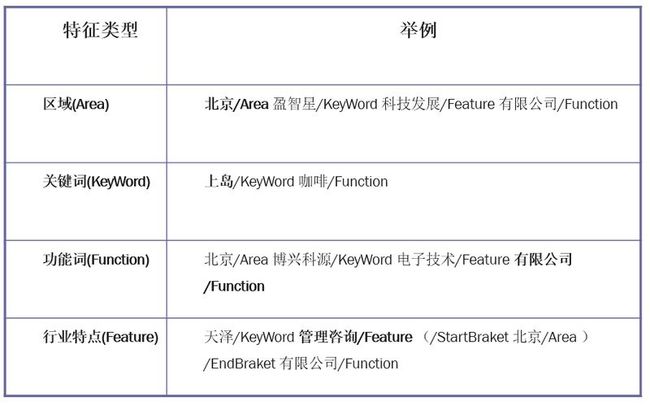
定义特征的类别:例如未登录词的上文,下文等。
根据特征词库对输入串做全切分:可以采用AdjList存储切分结果。
匹配规则来识别未登录词:可以把右边的模式组织成Trie树,左边的模式作为节点属性。全切分词图匹配上右边的模式后用左边的模式替换。
循环替换导致死锁
规则替换可能会进入死循环,因为可能出现重复应用规则的情况
A ->B ->A
通过检查每条规则来解决死锁问题
每个模式赋一个权重 ,用模式中的类型序列的权重和来衡量模式权重例如:
SuffixTown + Unknow + No +SuffixStreet = 6 + 8+ 5 + 7 = 26
SuffixTown + Street = 6 + 4 = 10
规则的左边的模式权重必须小于右边模式权重
应用这样的规则后整个文本的模式权重越来越小
从词图中匹配识别规则
根据基本词典生成的全切分词图
根据人名特征词图生成的人名全切分词图
根据译名特征词图生成的译名全切分词图
根据地名特征词图生成的地名全切分词图
根据机构名特征词图生成的机构名全切分词图
识别人名
人名特征:
单姓:赵 钱 孙 李
复姓:诸葛 欧阳
单名:刚 强 进 选 达
双名首字:建 建 治
双名尾字:军 红 国
日本姓:小泽 松下
日本名:田一郎 森三郎
译名用字:汤 姆 森 杰 克 妮
上文:邀请 约
下文:同学 老师
连接:和
根据音调判断是否人名
中文起名会考虑到语音的因素。例如:
Yang2 yang2
杨 阳
都是第二声。简称:22
可以统计中文人名的声调组合:
11=394
111=252
112=393
113=101
114=178
12=396
121=344
122=344
123=82
识别地名
地名相关的特征类型:
public enum AddressType {
Country //国家
,Municipality //直辖市
,SuffixMunicipality //特别行政区后缀
,Province //省
,City //市
,County //区
,Town //镇
,Street //街
,StreetNo //街门牌号
,No //编号
,Symbol //字母符号
,LandMark //地标建筑 例如 ** 大厦 门牌设施
,RelatedPos //相对位置
,Crossing //交叉路
,Village //村
,BuildingNo //楼号
,BuildingUnit //楼单元
,SuffixBuildingUnit //楼单元后缀
,SuffixBuildingNo //楼号后缀
,StartSuffix//(
,EndSuffix//)
,Unknow
…
}
识别译名
译名举例
费德勒 辛德勒 柴可夫斯基 卡钦斯基
统计译名用字,然后根据65万译名统计字之间的转移概率,例如”汤姆”、“珍妮”
P(C1C2…Cn)=P(C1) P(C2|C1)…P(Cn|C1C2…Cn-1)
≈P(C1) P(C2|C1)…P(Cn|Cn-1)
识别机构名
未登录词概率估计
P(某个未登录词的概率)=
P(这类未登录词的概率)*P(这类未登录词中某个词的概率)
在人名代词附近有更高的人名概率
杨士春表示,考虑到两人的特殊身份,谭维维和王铮亮并不担任日常的教学工作,他们的工作主要包括:...。
新词发现
有研究显示,60%的分词错误是由新词导致的。
旧词新意:通过各种途径产生的、具有基本词汇所没有的新形式、新意义或新用法的词语。
全新词语:自某一时间点以来所首次出现的具有新词形的词汇。如果在一篇文档中“水”和“立方”结合紧密,则有“水立方”可能是一个新词。
因此对分词后的词序列建立二元统计模型。结合紧密的二元连接可能是新词。
基于统计的新词发现
判断二元连接词结合紧密程度的公式:
如果词x和y的出现相互独立,则P(x,y)的值和p(x)p(y)的值相等,I(x,y)为0。如果x和y密切相关,P (x,y)将比P (x) P (y)大很多,I(x,y)值也就远大于0。如果x和y的几乎不会相邻出现,而它们各自出现的概率又比较大,那么I(x,y)将取负值,这时候x和y负相关。设f(C)是词C出现的次数,N是一个文档的总词数,则:
因此,两个词的信息熵:
新词发现实现
定义二元连接串:
public class Bigram {
String one;//上一个词
String two;//下一个词
private int hashvalue = 0;
Bigram(String first, String second) {
this.one = first;
this.two = second;
this.hashvalue = (one.hashCode() ^ two.hashCode());
}
}
int index = 0;
fullResults = new BigramsCounts[table.size()];
Bigrams key;
int freq;//频率
double logn = Math.log((double)n)/Math.log(2.0); //文档的总词数取对数
double temp;
double entropy;//信息熵
int bigramCount; //f(c1,c2)
for( Entry<Bigrams,int[]> e : table.entrySet()){//计算每个二元连接串的信息熵
key = e.getKey();
freq1 = oneFreq.get(key.one).freq;
freq2 = oneFreq.get(key.two).freq;
temp = Math.log((double)freq1)/Math.log(2.0) + Math.log((double)freq2)/Math.log(2.0);
bigramCount = (e.getValue())[0];
entropy = logn+Math.log((double)bigramCount)/Math.log(2.0) - temp;//信息熵
fullResults[index++] =
new BigramsCounts(
bigramCount,
entropy,
key.one,
key.two);
}
基于规则的方法:
具有普遍意义的构词规则,例如“模仿秀”由“动词+名词”组成。
去除规则,符合去除规则的二元连接不算作新词:
例如“数词+量词”的组合。