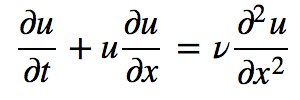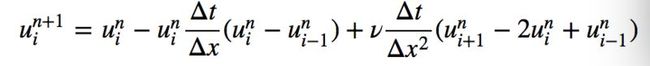Burgers方程形式
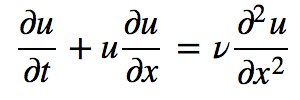
差分离散格式(forward difference for time,
backward difference for space
2nd-order method for the second derivatives )
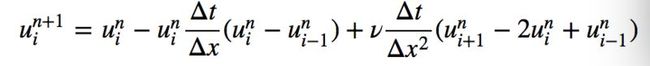
这里设置了周期性初始条件

#!/usr/bin/python
# -*-coding:utf-8 -*-
import numpy as np
import sympy
from sympy import init_printing
init_printing(use_latex=True) #在ipython中直接打印公式使用latex格式
from sympy.utilities.lambdify import lambdify
import matplotlib.pylab as plt
x,nu,t = sympy.symbols("x,nu,t")
phi = sympy.exp(-(x-4*t)**2/(4*nu*(t+1))) + sympy.exp(-(x-4*t-2*np.pi)**2/(4*nu*(t+1)))
phiprime = phi.diff(x)
u = -2*nu*(phiprime/phi)+4
ufunc = lambdify((t,x,nu),u)
nx = 101
nt=100
dx = 2*np.pi/(nx-1)
nu=0.07
dt=dx*nu
x= np.linspace(0,2*np.pi,nx)
un = np.empty(nx)
t=0
u=np.asarray([ufunc(t,x0,nu) for x0 in x]) #list 转化成 np.array
plt.figure(figsize=(4,4),dpi=100)
plt.plot(x,u,lw=2)
plt.xlim([0,2*np.pi])
plt.ylim([0,8])
for n in range(nt):
un = u.copy()
for i in range(nx-1):
u[i] = un[i] - un[i] * dt/dx *(un[i] - un[i-1]) + nu*dt/dx**2*(un[i+1]-2*un[i]+un[i-1])
u[-1] = un[-1] - un[-1] * dt/dx * (un[-1] - un[-2]) + nu*dt/dx**2*(un[0]-2*un[-1]+un[-2])
u_analytical = np.asarray([ufunc(nt*dt,xi,nu) for xi in x])
plt.figure(figsize=(6,6),dpi=100)
plt.plot(x,u,marker="o",color="blue",lw=2,label='Computational')
plt.plot(x,u_analytical,color="yellow",label='analytical')
plt.xlim([0,2*np.pi])
plt.ylim([0,10])
plt.legend()
plt.show()
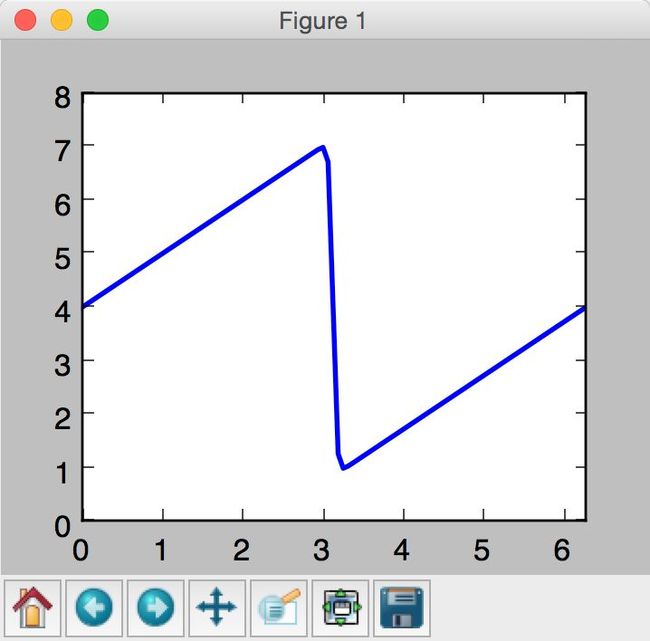
结果第一张图是初始图像,第二张是解析解和计算解比较图