浅谈RMXP自动地图元件的绘制原理
浅谈RMXP自动地图元件的绘制原理
作者:gouki04(啊古) 撰写日期:2011-12-27
博客链接:http://blog.csdn.net/gouki04
序:最近刚好想写个类似RMXP的地图编辑器,遇到的第一个问题就是自动地图元件的绘制问题。老实说,我不知道这东西到底叫什么(特别是英文叫什么),只知道RMXP翻译过来就是自动地图元件,而且魔兽的地图编辑器也用到这种技术,但我在网上却始终找不到相关的资料。其绘制原理其实很清晰,就是用户给出指定规格的地图元件资源,编辑器将其拆分,在绘制时再根据绘图上下文来进行拼接。但具体的过程以及拆分和拼接原理却很少有人提及,这里我整理了一下。
1.RMXP的自动地图元件规格
首先介绍下RMXP的自动地图元件规格,其中第一格和第二格都是展示用的,并不用在具体的拼接上。话说我也是刚搞懂的。
图1
真正用在拼接的就是剩下的内容,这里先将其按下图拆分开
图2
这里的每一个小格就是最后用于拼接的格子,我们暂且叫它小元件,如图每一个小元件都有一个编号,虽然编号为0,1,2,3,6,7,8的小元件都不会用到,但这样可以方便由编号来进行定位小元件的矩形。
计算编号为i的小元件在图中的矩形的方法为:
size = 16 // 小元件的宽高
row = i / 6 // 小元件所在的行
col = i % 6 // 小元件所在的列
(col * size, row * size, size, size)
2.分析所有拼接情况
在RMXP中,双击自动地图元件,即可以打开自动展开元件的对话框。里面显示的就是所有拼接情况。
图3
同样的,我们给每一种情况定一个编号
图4
注意,最后2个情况是一样的,所以总共有47种情况(编号从0开始)。每一种情况都是由4个小元件拼成的。这里先不急着确定每一种对应哪4个小元件。先来分析下到底是哪47种情况。假设我们现在正在用RMXP的地图编辑器来绘制自动地图元件,如下图,我们打算在位置4绘制一个自动地图元件
图5
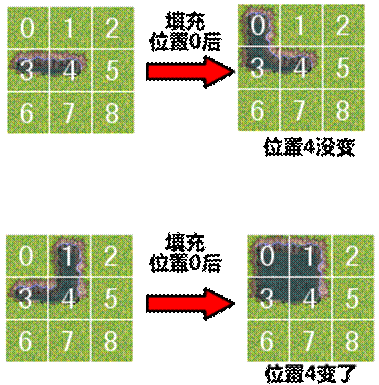
那么怎么判断绘制出来的是哪个情况呢?很简单,根据周围的0,1,2,3,5,6,7,8,格子是否有自动地图元件来确定位置4的绘制情况。(这里要注意,影响位置4绘制情况的是周围8个格子是否有自动地图元件,而每个格子具体是哪个情况并不影响)按照排列组合公式,可以算出8个格子的出现组合有256种,这比47大多了。为什么呢?这是因为RMXP并不支持对角连接,如下图
1和4位置的自动地图元件并不连接起来,也就是说此时1位置并不会影响4位置的绘制情况。那什么时候才会影响呢?看下图:
图7
可以看到,当位置1和3同时存在时,位置0才会影响到位置4。也就是说:当左边和上边都存在时,左上角才有影响力。同理可得:当左边不存在时,左上角和左下角都将失去影响力。(注意这点,后面就是靠这条理论来列举情况的)现在来列举所有情况。可以不考虑对角,只考虑边的组合。4边的组合有16种,可以分为5类:
1. 4边都没有(1种)
此时对角全失去影响力。位置4只有1种情况,即情况编号46
2. 只有1边(4种)
此时对角依然全失去影响力。位置4只有4种情况,即情况42,43,44,45
3. 有2边(6种)
3.1 对边情况(2种)
即左边和右边同时出现,或者上边和下边同时出现,此时对角依然全失去影响力。位置4只有2种情况,即情况32,33
3.2 临边情况(4种)
考虑左边和上边同时出现,此时左上角有影响力,有左上角出现与不出现2种情况。其他临边情况一样。位置4共有4*2=8种情况,即情况34-41
4. 有3边(4种)
考虑左上右同时出现,此时左上角和右上角有影响力,2个角有4种出现情况。所以共有4*4=16种情况。即情况16-31
5. 4边都有(1种)
此时所有角都有影响力,4个角有16种出现情况。所以共有1*16=16种情况。即情况0-15
上面的解析有点绕口,大家可以参考图4理解一下。
所有情况加起来刚好47种。
分析好了所有情况,就可以列出每一种情况对应的哪4个小元件
下面把我辛苦写出来的对应表给出:
等号左边为情况编号,右边为小元件表,注意小元件表里面小元件的顺序,是以
“左上,右上,左下,右下”的顺序的。
[0] = [26,27,32,33]
[1] = [4,27,32,33]
[2] = [26,5,32,33]
[3] = [4,5,32,33]
[4] = [26,27,32,11]
[5] = [4,27,32,11]
[6] = [26,5,32,11]
[7] = [4,5,32,11]
[8] = [26,27,10,33]
[9] = [4,27,10,33]
[10] = [26,5,10,33]
[11] = [4,5,10,33]
[12] = [26,27,10,11]
[13] = [4,27,10,11]
[14] = [26,5,10,11]
[15] = [4,5,10,11]
[16] = [24,25,30,31]
[17] = [24,5,30,31]
[18] = [24,25,30,11]
[19] = [24,5,30,11]
[20] = [14,15,20,21]
[21] = [14,15,20,11]
[22] = [14,15,10,21]
[23] = [14,15,10,11]
[24] = [28,29,34,35]
[25] = [28,29,10,35]
[26] = [4,29,34,35]
[27] = [4,29,10,35]
[28] = [26,27,44,45]
[29] = [4,39,44,45]
[30] = [38,5,44,45]
[31] = [4,5,44,45]
[32] = [24,29,30,35]
[33] = [14,15,44,45]
[34] = [12,13,18,19]
[35] = [12,13,18,11]
[36] = [16,17,22,23]
[37] = [16,17,10,23]
[38] = [40,41,46,47]
[39] = [4,41,46,47]
[40] = [36,37,42,43]
[41] = [36,5,42,43]
[42] = [12,17,18,23]
[43] = [12,13,42,43]
[44] = [36,41,42,47]
[45] = [16,17,46,47]
[46] = [12,17,42,47]
[47] = [12,17,42,47]
3.绘制
绘制的过程大概是以下伪代码
// 在row行,col列绘制一个自动地图元件
void drawAt(int row, int col)
{
// 判断row和col是否越界
// 将[row,col]位置填为47号情况
// 这里可以填任意情况,只要确保[row,col]位置不为空即可
drawTileIndex(row,col,47);
// 更新[row,col]以及其周围8个格子的状态
updateTileState(row,col);
updateTileState(row-1,col-1);
updateTileState(row-1,col);
updateTileState(row-1,col+1);
updateTileState(row,col-1);
updateTileState(row,col+1);
updateTileState(row+1,col-1);
updateTileState(row+1,col);
updateTileState(row+1,col+1);
}
void drawTileIndex(int row, int col, int index)
{
// 根据index得到对应的小元件表
// 根据小元件表拼接成地图元件
}
void updateTileState(int row, int col)
{
// 如果该位置没有地图元件,则直接返回
if (!hasTileAt(row,col)) return;
// 判断其周围8个格子的状态state
// 根据判断的状态确定情况的编号index
drawTileIndex(row,col,index);
}
这里最麻烦的就是“根据判断的状态确定情况的编号index”
由于情况有47种之多,而且判断的过程也很纠结。这里提供我的方法,虽然也很麻烦,不过逻辑比较清晰。
核心就是用二进制表达,边角共有8个,用一个8位的char即可。首先定义如下:4边4角各占一位
left = 0000 0001
right = 0000 0010
top = 0000 0100
bottom = 0000 1000
left_top = 0001 0000
right_top = 0010 0000
left_bottom = 0100 0000
right_bottom = 1000 0000
那么当前4边4角的情况就可以上面的组合出来。
然后就可以用switch case表达47种情况,如
switch(state)
{
case 1111 1111: /*即4边4角都有*/ index = 0; break;
case 1100 1000: /*即左边和上边以及左上角都有*/ index = 38; break;
...
}
4.小结
没想到写这样一篇文章会这么费力,在写这家伙时,我总感觉自己的方法太笨了。我感觉会有好的方法的,所以还是坚持写下来,抛砖引玉了。