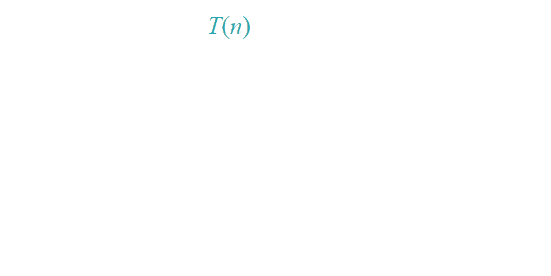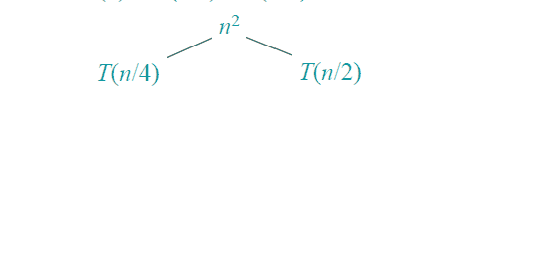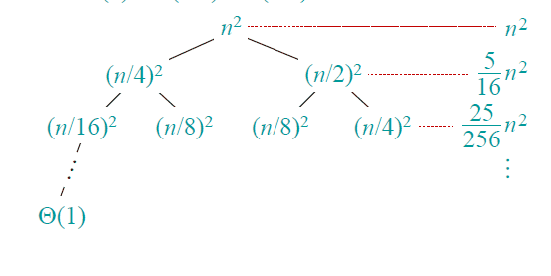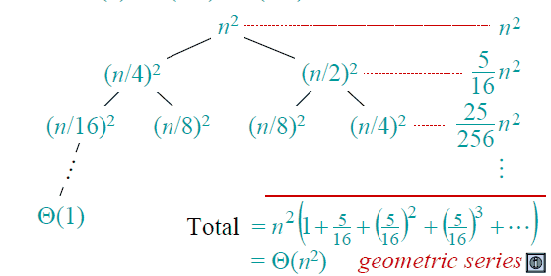算法打基础——符号&递归解法
第二节 算法复杂度分析的的基本符号及 递归关系式下的复杂度解法
这次的主要知识点是:
1.各种复杂度符号 2.递归复杂度解法: 分为三种 替换法(猜!) 递归树法 主定理
1各种复杂度符号
big O definition:
O(g(n))= { f(n) : there exist constants c>0, n0>0 such that 0<=f(n)<=cg(n) for all n>=n0}
big Ω definition:
Ω(g(n))= { f(n): there exist constants c>0, n0>0 such that 0<=cg(n)<=f(n) for all n>=n0}
big Θ definition:
Θ(g(n)) = O(g(n)) ∩Ω(g(n))
some small notation
small o definition:
ο(g(n))= { f(n) : for any constant c>0, there is a constant n0>0 such that 0<=f(n)<cg(n) for all n>=n0}
small ω definiton:
ω(g(n))= { f(n): for any constant c>0, there is a constant n0>0 such that 0<=cg(n)<f(n) for all n>=n0}
2 递归求解
递归的求解方法在教程中提到了3种: 替换法、递归树 和 主定理(叫主定理是因为它是主要用到的定理)
下面分别讲这三个定理:
替换法:其重要的过程就是猜,假设! 假设一个复杂度,然后进行证明
其过程是: 1. 猜 解的形式
2. 通过归纳法 验证
3. 得出使解真正有效的常数
解法的一个例子见我的算法笔记,里面有详细的推导。
递归树: 递归树方法并不是一个严格的证明,只是一种启发性的思路。它可以作为替换法的猜测的来源
上一节就有一个递归树的例子,这一节在给出一个更复杂的例子:
解: T(n) = T(n/4)+T(n/2)+n2:
主定理: 主定理是非常重要的.他可以解决很多递归问题,但是也没有完全覆盖所有的情况。它分为三种
情况,需要记好多东西。。。
主定理是应用到下面形式的递归上的:
T(n) = aT(n/b)+f(n), 其中 a>=1,b>1:
比较f(n)和nlogba 根据比较的情况分为三种情况:
1. f(n) = O(nlogba-ε) for 某个常数ε>0.
这个条件是指 f(n) 以 nlogba 比是多项式级别慢的
其解为: T(n) = Θ(nlogba)
2. f(n)=Θ(nlogbalgkn) 对常数k>=0.
这个条件是指f(n)和 nlogba是以相似的速度在增长的
其解为: T(n)=Θ(nlogbalgk+1n).
3. f(n)= Ω(nlogba+ε) for 某个常数ε>0.
这个条件是指f(n)增长的比 nlogba快
而且!需要f(n)满足一个正则条件:af(n/b)<=cf(n) for 某常数c<1
其解为:T(n)=Θ(f(n))
主定理可以通过递归树很好的理解与证明!比如 第三种情况那个正则条件怎么来的等。
然后我们来通过递归树来分析一下主定理: