[Math]PHI, the golden ratio

PHI, the golden ratio 黄金分割比

转载自 http://paulbourke.net/miscellaneous/miscnumbers/

1. Definition

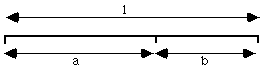
将一个线段分成两段，那么长的部分与短的那部分的比率等于整个线段与长的部分的比率时，

      　　　　　　

这个条件可被解释为 $\frac{a}{1-a}=\frac{1}{a}$.即如下的二项式： $a^2+a-1=0$,方程有两个解, $-\phi$,和$\phi-1$。

$$\therefore \phi = \frac{\sqrt{5}+1}{2} \approx 1.618$$
这是古希腊数学中初始定义，我们一般用$\phi-1$
$$\phi-1 = \frac{\sqrt{5}-1}{2} \approx 0.618$$

2. 常见关系式

\begin{align*}
& \phi^2=1+\phi \qquad \phi^3 = 1+2\phi\\
& \frac{1}{\phi}=\phi-1 \qquad \frac{1}{\phi^2} = 2-\phi\\
& \sin(18)=\frac{\phi-1}{2} \qquad \cos(36)=\frac{\phi}{2}\\
& \phi^{x+1}=\phi^{x}+\phi^{x-1}
\end{align*}

3. Continued_fraction 连分式

关于一些常见连分式，参见Wiki之Continued_fraction . 

　　　　　　　　

phi = sqrt(1 + sqrt(1 + sqrt(1 + sqrt(1 + .....))))

4. Relationship to the Fibonnaci series

(1).Ratio

当斐波那契数列趋向$\infty$时，$a_{n-1}/a_{n}$趋近于$\phi-1$

\begin{align*}
&1\quad 1\quad 2\quad 3\quad 5\quad 8\quad 13\quad 21\quad 34\quad 55\quad 89\cdots\\
&1\quad 0.5 \quad 0.67 \quad 0.6\quad 0.625 \quad 0.6154 \quad 0.619 \quad 0.6176\quad 0.6182\cdots
\end{align*}

(2).Phi Fibonnaci series

数列满足下面两个条件：

\begin{align*}
&(a).u_{n+1}=u_{n}+u_{n-1}\\
&(b).\frac{u_{n+1}}{u_{n}}=constant\\
\end{align*}

 验证可知，这样的数列有且仅有一个： 
$$1,phi,1+phi,2+3phi,3+5phi,5+6phi,\cdots$$

5. 2 dimensional golden ratio 二维黄金分割比

由原来的一维线段归纳推导出来的定义为: "find a rectangle such that when a square is removed the remaining rectangle has the same proportions as the original". The solution to this is a rectangle with the ratio of its sides being phi.

　　　　　　　　

These rectangles can be inscribed in a so called logarithmic(对数的) spiral(螺旋) also known as equiangular(等角) spirals. Such spirals and occur frequently in nature, for example: shells(贝壳), sunflowers, and pine cones(松果). The limit point of the spiral is called the "eye of God".

6.Phi Pyramid