图解缓存淘汰算法一之LRU

1.概念分析

       LRU(Least Recently Used),即最近最少使用.怎么理解这个概念呢?我一开始见到这个概念的时候,以为"最近","最少"都是修饰使用的(从中文解释中可以看出),不过这种理解是错误的,最近是修饰最少的,故应该理解为"最近这段时间最少访问的,最少使用".

      这样理解是不是更清晰一些呢?也就是说,LRU这种算法是会将近期最少使用的数据淘汰掉.这样说的话,LRU淘汰算法似乎是将最近次数上使用最少的数据淘汰^[1],其实不然,或者说理解的不确切,更准确地说,LRU算法是将近期最不会访问的数据淘汰掉^[2](请注意[1]和[2]的不同,[1]处注重了次数上的比较,[2]处却没有这层意义).它的核心思想是"如果数据最近被访问过,那么将来被访问的概率也很高".反过来说,"如果数据最近这段时间一直都没有访问,那么将来被访问的概率也会很低".Well,我知道这两句都是伪命题,就好像说一个人最近一直倒霉,那么他一辈子都会倒霉.不过,LRU就是基于这种思想来的.如果一个指导思想本身就有很多问题,那么在指导现实行为时就更加荒唐了(似乎有点形而上学的意味了...).

      因此,我们在这里可以说,LRU是荒唐的,是简单粗暴的,是片面的.打住,似乎变成了LRU的批斗会了.

      --那么LRU就一无是处了?

      --不是的.LRU算法的优点在于简单,而且也可以解决一些实际问题.只不过没那么精确而已,很多时候LRU算法也会有不少冤假错案,本来不该剔除的数据就白白的牺牲掉了.但是我们还是要正式LRU的优点.

      下面就讲解LRU的算法实现.

2.原理

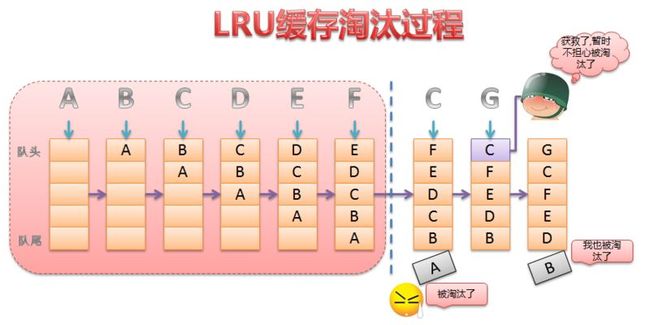
我画了一个LRU淘汰算法的过程图:

 

 下面简单讲解一下(需要在这里说明一下,LRU一般采用链表方式实现,便于快速移动数据位置,虽然图中使用似乎是数组方式):

1. 一开始,缓存池是空的,缓存池中插入数据时不用担心容量不足的事情.因此这个过程就是类似队列的FIFO(但不止这些);
2. 在第5步将E插入到缓存池中后,缓存池已经满了(当然实际应用中不会让到达缓存池的尺寸,一般到70%左右就要考虑淘汰机制了);
3. 当第6步将E插入缓存池的时候,发现缓存池已经满了,LRU会将最早加入到缓存池的数据淘汰掉(A,实在不要意思啊);
4. 第7步,从缓存池中访问C,C被访问,从时间点上是最近最近访问的,将C移动到链表的头部(C侥幸暂时远离被淘汰的边缘);
5. 第8步,将G插入缓存池中,G处于链表头部,B不幸被淘汰.

大致的过程就是这样,关于淘汰机制只是后面的三步中会用到,画出前面六步的过程只是说明,LRU插入元素的方式.在这个图中,我想大家应该可以明白为什么使用链表,而不使用数组(链表的插入和删除的时间复杂度都是O(1)).

3.优劣分析

 【命中率】

命中率较高,不过偶发性的情况对LRU的命中影响很大,同时也会引入很多数据污染(比如很长时间只访问一次的数据,在后期的文章中会涉及到这一话题,会有改进的方案).

 【复杂度】

实现起来较为简单.

 【存储成本】

几乎没有空间上浪费.

 【缺陷】

仅仅从最近使用时间上考虑淘汰算法,没有考虑缓存单元的使用频率,可能会淘汰一些仍有价值的单元.

4.实现

暂时略,以后会采用伪代码和java语言的方式做简单的实现.

最后,如有哪里不正确的地方,请多多指教. 后续会将其他缓存淘汰算法一一介绍,敬请期待.

 

 相关文章:

1. 缓存算法
2. 缓存淘汰算法系列之1——LRU类