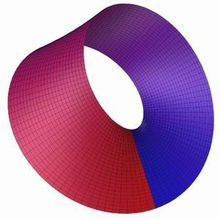
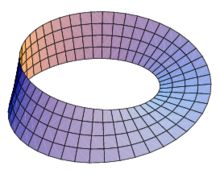
麦比乌斯圈
麦比乌斯圈(Möbius strip, Möbius band)是一种单侧、不可定向的曲面。因A.F.麦比乌斯(August Ferdinand Möbius, 1790-1868)发现而得名。将一个长方形纸条ABCD的一端AB固定,另一端DC扭转半周后,把AB和CD粘合在一起 ,得到的曲面就是麦比乌斯圈,也称麦比乌斯带。
目录
编辑本段简单解释麦比乌斯圈
想象一下一长条卫生纸,把它首尾相连,不要粘起来,就会发现原来的一面与其反面相连。对于中小学生来说,多制作几次麦比乌斯圈有助于理解。麦比乌斯圈
编辑本段故事
数学上流传着这样一个故事:有人曾提出,先用一张长方形的纸条,首尾相粘,做成一个纸圈,然后只允许用一种颜色,在纸圈上的一面涂抹,最后把整个纸圈全部抹成一种颜色,不留下任何空白。这个纸圈应该怎样粘?如果是纸条的首尾相粘做成的纸圈有两个 面,势必要涂完一个面再重新涂另一个面,不符合涂抹的要求,能不能做成只有一个面、一条封闭曲线做 边界的纸圈儿呢?莫比乌斯环
编辑本段莫比乌斯带的发现
对于这样一个看来十分简单的问题,数百年间,曾有许多 科学家进行了认真研究,结果都没有成功。后来, 德国的 数学家莫比乌斯对此发生了浓厚兴趣,他长时间专心思索、 试验,也毫无结果。有一天,他被这个问题弄得头昏脑涨了,便到野外去散步。新鲜的空气,清凉的风,使他顿时感到轻松舒适,但他头脑里仍然只有那个尚未找到的圈儿。
一片片肥大的玉米叶子,在他眼里变成了“绿色的纸条儿”,他不由自主地蹲下去,摆弄着、观察着。叶子弯曲着耷拉下来,有许多扭成半圆形的,他随便撕下一片,顺着叶子自然扭的方向对接成一个圆圈儿,他惊喜地发现,这“绿色的圆圈儿”就是他梦寐以求的那种圆圈。
莫比乌斯回到办公室,裁出纸条,把纸的一端扭转180°,再将一端的正面和背面粘在一起,这样就做成了只有一个面的纸圈儿。
圆圈做成后,莫比乌斯捉了一只小甲虫,放在上面让它爬。结果,小甲虫不翻越任何边界就爬遍了圆圈儿的所有部分。莫比乌斯激动地说:“公正的小甲虫,你无可辩驳地证明了这个圈儿只有一个面。” 麦比乌斯圈就这样被发现了。
做几个简单的实验,就会发现“麦比乌斯圈”有许多让我们感到惊奇而有趣的结果。弄好一个圈,粘好,绕一圈后可以发现,另一个面的入口被堵住了,原理就是这样啊.
实验一
如果在裁好的一张纸条正中间画一条线,粘成“莫比乌斯带”,再沿线剪开,把这个圈 一分为二,照理应得到两个圈儿,奇怪的是,剪开后竟是一个大圈儿。实验二
如果在纸条上划两条线,把纸条三 等分,再粘成“莫比乌斯带”,用剪刀沿画线剪开,剪刀绕两个圈竟然又回到原出发点,猜一猜,剪开后的结果是什么,是一个大圈?还是三个圈儿?都不是。它究竟是什么呢?你自己动手做这个实验就知道了。你就会惊奇地发现,纸带不是一分为二,而是一大一小的相扣环。有趣的是:新得到的这个较长的纸圈,本身却是一个双侧曲面,它的两条边界自身虽不打结,但却相互套在一起。我们可以把上述纸圈,再一次沿中线剪开,这回可真的一分为二了!得到的是两条互相套着的纸圈,而原先的两条边界,则分别包含于两条纸圈之中,只是每条纸圈本身并不打结罢了。
关于莫比乌斯带的单侧性,可如下直观地了解,如果给莫比乌斯带着色,色笔始终沿曲面移动,且不越过它的边界,最后可把莫比乌斯圈两面均涂上颜色 ,即区分不出何是正面,何是反面。对圆柱面则不同,在一侧着色不通过边界不可能对另一侧也着色。单侧性又称不可定向性。以曲面上除边缘外的每一点为圆心各画一个小圆,对每个小圆周指定一个方向,称为相伴麦比乌斯圈单侧曲面圆心点的指向,若能使相邻两点相伴的指向相同,则称曲面可定向,否则称为不可定向。麦比乌斯圈是不可定向的。
莫比乌斯圈还有着更为奇异的特性。一些在平面上无法解决的问题,却不可思议地在麦比乌斯圈上获得了解决。比如在普通空间无法实现的“手套易位问题”:人左右两手的手套虽然极为相像,但却有着本质的不同。我们不可能把左手的手套贴切地戴到右手上去;也不能把右手的手套贴切地戴到左手上来。无论你怎么扭来转去,左手套永远是左手套,右手套也永远是右手套。不过,倘若你把它搬到麦比乌斯圈上来,那么解决起来就易如反掌了。
“手套移位问题”告诉我们:堵塞在一个扭曲了的面上,左、右手系的物体可以通过扭曲实现转换。让我们展开想象的翅膀,设想我们的空间在宇宙的某个边缘,呈现出麦比乌斯圈式的弯曲。那么,有朝一日,我们的星际宇航员会带着左胸腔的心脏出发,却带着右胸腔的心脏返回地球呢!瞧,麦比乌斯圈是多么的神奇!但是,麦比乌斯圈具有一条非常明显的边界。这似乎是一种美中不足。公元1882年,另一位德国数学家费力克斯·克莱茵(Felix Klein,1849~1925),终于找到了一种自我封闭而没有明显边界的模型,后来以他的名字命名为“克莱因瓶”。这种怪瓶实际上可以看作是由一对麦比乌斯圈,沿边界粘合而成。
“麦比乌斯带”有点神秘,一时又派不上用场,但是人们还是根据它的特性编出了一些故事,据说有一个小偷偷了一位很老实农民的东西,并被当场捕获,将小偷送到县衙,县官发现小偷正是自己的儿子。于是在一张纸条的正面写上:小偷应当放掉,而在纸的反面写了:农民应当关押。县官将纸条交给执事官由他去办理。聪明的执事官将纸条扭了个弯,用手指将两端捏在一起。然后向大家宣布:根据县太爷的命令应当放掉农民,应当关押小偷。县官听了大怒,责问执事官。执事官将纸条捏在手上给县官看,从“应当”二字读起,确实没错。仔细观看字迹,也没有涂改,县官不知其中奥秘,只好自认倒霉。
县官知道执事官在纸条上做了手脚,怀恨在心,伺机报复。一日,又拿了一张纸条,要执事官一笔将正反两面涂黑,否则就要将其拘役。执事官不慌不忙地把纸条扭了一下,粘住两端,提笔在纸环上一划,又拆开两端,只见纸条正反面均涂上黑色。县官的毒计又落空了。
现实可能根本不会发生这样的故事,但是这个故事却很好地反映出“莫比乌斯带”的特点。
编辑本段麦比乌斯环
奇妙之处有三
一、麦比乌斯环只存在一个面。二、如果沿着麦比乌斯环的中间剪开,将会形成一个比原来的麦比乌斯环空间大一倍的、把纸带的端头扭转了四次再结合的环(并不是莫比乌斯带,在本文中将之编号为:环0),而不是形成两个麦比乌斯环或两个其它形式的环。
三、如果再沿着环0的中间剪开,将会形成两个与环0空间一样的、具有正反两个面的环,且这两个环是相互套在一起的(在本文中将之编号为:环1和环2),从此以后再沿着环1和环2以及因沿着环1和环2中间剪开所生成的所有环的中间剪开,都将会形成两个与环0空间一样的、具有正反两个面的环,永无止境……且所生成的所有的环都将套在一起,永远无法分开、永远也不可能与其它的环不发生联系而独立存在。
六个特征
麦比乌斯环0和生成的所有的环的六个特征:一、麦比乌斯环是通过将正反面其中的一端反转180度与另一端对接形成的,也因此它将正反面统一为一个面,但也因此而存在了一个“拧劲”,我们在此不妨称之为“麦比乌斯环拧劲”1。
二、从麦比乌斯环生成为环0需要一个“演变的裂变”过程,此“演变的裂变”过程将“麦比乌斯环拧劲”分解成了因“相通”或“相连”从而分别呈现出“螺旋弧”向下和“螺旋弧”向上两个方向“拧”的四个“拧劲”。这四个“拧劲”中的第一个和第三个的“拧劲”将正面转化为反面,而第二个和第四个的“拧劲”再将反面转化为正面,或者说是,这四个的“拧劲”中的第一个和第三个的“拧劲”将反面转化为正面,而第二个和第四个的“拧劲”再将正面转化为反面,使所生成的环0从而存在了“正反”两个面。
三、从麦比乌斯环生成为环0的过程,还使环0具有了因相互转换而最终呈现为同一个方向上的、性质不同的四个“拧劲”。“演变的裂变”过程将麦比乌斯环的“麦比乌斯拧劲”分解成环0中的四个“拧劲”,“麦比乌斯拧劲”的“能”也被生成了环0中的这四个“拧劲”的“能”,但环0中的这四个“拧劲”的“能”是“麦比乌斯拧劲”的“能”2倍,新生成的1倍于“麦比乌斯拧劲”的“能”的方向与原来的“麦比乌斯拧劲”的“能”的方向相反。
四、从麦比乌斯环生成为环0的过程,还使环0的空间比麦比乌斯环的空间增大了一倍。
五、从环0生成环n和环n+1的过程,环0中的四个“拧劲”的“能”不会增加,但从环0的“裂变”中,每“裂变”一次会增加一个环0的空间。
六、从环0生成环1和环2以及再“裂变”直至环n和环n+1后,所生成的所有的环n和环n+1都将套在一起,永远无法分开、永远也不可能与其它的环不发生联系而独立存在。
奇妙的启示
从麦比乌斯环的三个奇妙之处和麦比乌斯环、环0以及生成的所有的环的六个特征,我们得到奇妙的启示:一、无论将麦比乌斯环放在宇宙时空的任何地方,我们同样也会发现麦比乌斯环之外的空间也只能是存在一个面,因此,宇宙时空的任何空间之处也只存在一个面。如果宇宙时空的任何空间之处只存在一个面,那么我们就可以认为宇宙时空中的任何一点与其它的点都是相通的,即整个宇宙时空是相通的,任何一点都是宇宙的中心,也是宇宙的边缘,宇宙时空中的任何物质也都是一样,也都处于宇宙的中心,也都处于宇宙的边缘。
二:宇宙时空中的任何一个点都可以通过“裂变”的方式无中生有地生成一个对立的阴阳两性。无论生成的这一个对立的阴阳两性是否需要载体呈现出来,通过“裂变”的方式,无中生有地、生成的一个对立的阴阳两性,都需要一个比原来的空间大一倍的空间,来体现这生成的、一个对立的阴阳两性。
三: 只要存在“裂变”就会使原来的麦比乌斯环不再以“本来面目”存在,或者说,原来的麦比乌斯环已经不存在了。从无中生有的、生成的、具有一个对立的、阴阳两性的环0“复原”成原来的麦比乌斯环,则需要化解一个对立的阴阳两性的面。
四、从麦比乌斯环生成为环0的过程,还使环0具有了因相互转换而最终呈现为同一个方向上的、性质不同的四个“拧劲”。我们得知,任何一个肯定应该是一个具有同一个方向上的、有缺口的或说成是非绝对的否定之否定之否定之否定的矢量(有一定方向的否定)过程。
五、从环0生成环1和环2以及再“裂变”直至环n和环n+1后,所生成的所有的环n和环n+1都将套在一起,永远无法分开、永远也不可能与其它的环不发生联系而独立存在。这说明宇宙万物之间存在普遍联系的法则,而且任何一点或一个事物都与其他所有的宇宙万物相通相连,是不可分割的、不可遗漏的。
六、宇宙万物从最终起源上来讲是没有任何差异的,均起源于只有一个面的空间或者说没有任何面的状态。因此也可以说宇宙万物都是从无中生有中而来,只不过是在演变的过程中呈现出差异而已。
七、在麦比乌斯环生成为环0的“裂变”过程中,无中生有的增加生成原有“拧劲”中的1倍的新的能量,也就是说在新产生的一对阴阳两性关系体的过程中的“裂变”不遵循“能量守恒原则”;而之后的所有的宇宙万物的再“裂变”只能使宇宙的时空增大,不再生成新的能量,而且在“裂变”中必然遵循“能量守恒原则”。
八、宇宙时空中的任何一个点都可以通过无中生有的方式第一次生成阴阳两性,然后再分别以刚生成的阴阳两性为基础生成第一次的阴阳两性的两个物质,第二次、第三次……直至永无穷尽。
编辑本段麦比乌斯圈与克莱因瓶
如果我们把两条麦比乌斯带沿着它们唯一的边粘合起来,你就得到了一个克莱因瓶(当然不要忘了,我们必须在 四维空间中才能真正有可能完成这个粘合,否则的话就不得不把纸撕破一点)。同样地,如果把一个克莱因瓶适当地剪开来,我们就能得到两条麦比乌斯带。除了我们上面看到的克莱因瓶的模样,还有一种不太为人所知的“8字形”克莱因瓶。它看起来和上面的曲面完全不同,但是在四维空间中它们其实就是同一个曲面——克莱因瓶。 实际上,可以说克莱因瓶是一个三度的麦比乌斯带。我们知道,在平面上画一个圆,再在圆内放一样东西,假如在二度空间中将它拿出来,就不得不越过圆周。但在三度空间中,很容易不越过圆周就将其拿出来,放到圆外。将物体的轨迹连同原来的圆投影到二度空间中,就是一个“二维克莱因瓶”,即麦比乌斯带(这里的麦比乌斯带是指拓扑意义上的麦比乌斯带)。再设想一下,在我们的三度空间中,不可能在不打破蛋壳的前提下从鸡蛋中取出蛋黄,但在四度空间里却可以。将蛋黄的轨迹连同蛋壳投影在三度空间中,必然可以看到一个克莱因瓶。 附:克莱因瓶在 三维空间中是破裂的,最少要有一个裂缝,如果有两个裂缝的话,它必然是两条部分相和连的麦比乌斯带,同样n条麦比乌斯带也可以组合成一个有n个裂缝克莱因瓶。编辑本段麦比乌斯圈的应用
麦比乌斯圈在数学中的应用
数学中有一个重要分支叫 拓扑学,主要是研究 几何图形连续改变形状时的一些特征和规律的,麦比乌斯圈变成了 拓扑学中最有趣的单侧面问题之一。麦比乌斯圈在实际生活中的运用
麦比乌斯圈的概念被广泛地应用到了 建筑, 艺术, 工业生产中。运用麦比乌斯圈原理我们可以建造 立交桥和 道路,避免车辆行人的拥堵。垃圾回收标志
一、1979年,美国著名轮胎公司百路驰创造性地把传送带制成麦比乌斯圈形状,这样一来,整条传送带环面各处均匀地
Power Architecture 标志
承受磨损,避免了普通传送带单面受损的情况,使得其寿命延长了整整一倍。
二、针式打印机靠打印针击打色带在纸上留下一个一个的墨点,为充分利用色带的全部表面,色带也常被设计成麦比乌斯圈。 三、在美国匹兹堡著名肯尼森林游乐园里,就有一部“加强版”的云霄飞车——它的轨道是一个麦比乌斯圈。乘客在轨道的两面上飞驰。
四、麦比乌斯圈循环往复的几何特征,蕴含着永恒、无限的意义,因此常被用于各类标志设计。微处理器厂商Power Architecture的商标就是一条麦比乌斯圈,甚至垃圾回收标志也是由麦比乌斯圈变化而来。
编辑本段几何学与拓扑学结构
一个利用参数方程式创造出立体麦比乌斯带的方法:用Matlab描绘的莫比乌斯带
x(u,v)=[1+v/2×cos(u/2)]cos(u)
y(u,v)=[1+v/2×cos(u/2)]sin(u)
z(u,v)=v/2×sin(u/2)
其中0≤u<2π且-1≤v≤1 。.这个方程组可以创造一个边长为1半径为1的麦比乌斯带,所处位置为x-y面,中心为(0,0,0)。参数u在v从一个边移动到另一边的时候环绕整个带子。
如果用极坐标方程表示的话(r,θ,z),一个无边界的麦比乌斯带可以表示为:
log(r)sin(θ/2)=zcos(θ/2)。
编辑本段麦比乌斯简介(1790~1868)
Möbius,August Ferdinand德国数学家,天文学家 。1790 年11月17日生于瑙姆堡附近的舒尔普福塔,1868年9月26日卒于莱比锡。1809 年入莱比锡大学学习法律,后转攻数学、物理和天文。1814 年获博士学位,1816年任副教授,1829年当选为柏林科学院通讯院士,1844年任莱比锡大学天文与高等力学教授。
麦比乌斯的科学贡献涉及天文和数学两大领域。他领导建立了莱比锡大学天文台并任台长。因发表《关于行星掩星的计算》而获得天文学家的赞誉,此外还著有《天文学原理》和《天体力学基础》等天文学著作。在数学方面,麦比乌斯发展了射影几何学的代数方法。他在其主要著作《重心计算》中 ,独立于 J. 普吕克等人而创立了代数射影几何的基本概念——齐次坐标。在同一著作中他还揭示了对偶原理与配极之间的关系,并对交比概念给出了完善的处理。麦比乌斯最为人知的数学发现是后来以他的名字命名的单侧曲面——麦比乌斯带。此外,麦比乌斯对拓扑学球面三角等其他数学分支也有重要贡献。
编辑本段艺术和科技
麦比乌斯带为很多 艺术家提供了灵感,比如美术家 毛瑞特斯·柯奈利斯·艾雪就是一个利用这个结构在他木刻画作品里面的人,最著名的就是麦比乌斯二代,图画中表现一些 蚂蚁在麦比乌斯带上面爬行。它也经常出现在科幻小说里面,比如亚瑟·克拉克的《黑暗之墙》。科幻小说常常想象我们的宇宙就是一个麦比乌斯带。由A.J.Deutsch创作的短篇小说《一个叫麦比乌斯的地铁站》为波士顿地铁站创造了一个新的行驶线路,整个线路按照麦比乌斯方式扭曲,走入这个线路的火车都消失不见。另外一部小说《星际航行:下一代》中也用到了麦比乌斯带空间的概念。
有一首小诗也描写了麦比乌斯带:
数学家断言 麦比乌斯带只有一边 如果你不相信 就请剪开一个验证 带子分离时候却还是相连 麦比乌斯带也被用于工业制造。一种从麦比乌斯带得到灵感的传送带能使用更长的时间,因为可以更好的利用整个带子,或者用于制造磁带,可以承载双倍的信息量。
有一座钢制的麦比乌斯带雕塑位于美国华盛顿的史密斯森林历史和技术博物馆。
荷兰建筑师Ben Van Berkel以麦比乌斯带为创作模型设计了著名的麦比乌斯住宅。
在日本漫画《哆啦A梦》中,哆啦A梦有个道具的外观就是麦比乌斯带;在故事中,只要将这个环套在门把上,则外面的人进来之后,看到的仍然是外面。
在日本的艾斯奥特曼第23话《逆转!佐菲登场》中TAC队利用麦比乌斯带的原理,让北斗和南进入异次元空间消灭了亚波人。
在电玩游戏 "音速小子 - 滑板流星故事" 中最后一关魔王战就是在麦比乌斯带形状的跑道上进行,如果你不打败魔王就会一直在麦比乌斯带上无限循环的滑下去.....
1988年在日本上映的动画电影机动战士高达 逆袭的夏亚以麦比乌斯带作为对命运的隐喻:人类就好比行走在麦比乌斯带上的蚂蚁一般,永远逃不出这个怪圈,不断重复着相同的错误,类同的悲剧也在不断地上演。 电影的主题歌BEYOND THE TIME (メビウスの宇宙を越えて) 亦呼应了这个主题(日文メビウス就是Möbius的意思)。
日本的梦比优斯奥特曼名字也取于麦比乌斯带,其变身是则为“无限”的标志,及剪开的麦比乌斯带。
词条图册更多图册
词条图片(6张)
- 参考资料
-
-
1. 莫比乌斯带——维基百科 .
-
- 扩展阅读:
-
- 1
《拓扑实验》
- 2
- 3
《博物》2009.08,总68期
- 1