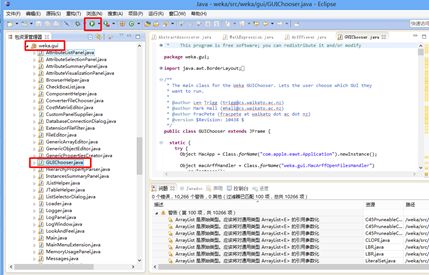
WEKA使用（基础配置+垃圾邮件过滤+聚类分析+关联挖掘）

声明：

1）本文由我bitpeach原创撰写，转载时请注明出处，侵权必究。

2）本小实验工作环境为Windows系统下的WEKA，实验内容主要有三部分，第一是分类挖掘（垃圾邮件过滤），第二是聚类分析，第三是关联挖掘。

3）本文由于过长，且实验报告内的评估观点有时不一定正确，希望抛砖引玉。

（一）WEKA在Ubuntu下的配置

下载解压

下载和解压weka
。下载：

创建目录：sudo mkdir /usr/weka。

解压weka到该目录：unzip weka-3-6-10.zip -d /usr/weka。

配置Ubuntu的环境变量

配置环境变量。还是使用vim 在/etc/environment 中配置。（新增WEKAROOT，修改CLASSPATH）

export WEKAROOT=/usr/weka/weka-3-6-10

export CLASSPATH=.:$JAVA_HOME/lib:$JAVA_HOME/jre/lib:$WEKAROOT/weka.jar

最后别忘了 source /etc/environment，加载新的配置文件。

当然了WEKAROOT换成别的名字也可以的，如WEKA_PATH等，切记如果想换名字的话，首先用echo命令查看环境变量参数，指令如下：

echo $WEKAROOT

然后使用unset命令删除掉，指令为unset WEKAROOT

最后新建一个WEKA_PATH环境，新建方法仍然是往environment文件里写入并更新。

运行WEKA

运行WEKA，运行命令：cd $WEKAROOT（或者cd $WEKA_PATH）

运行命令：java -Xmx1000M -jar weka.jar（或者java -jar weka.jar）

Java虚拟机进程能构从操作系统那里挖到的最大的内存，以字节为单位，如果在运行java程序的时候，没有添加-Xmx参数，那么就是64兆，这是java虚拟机默认情况下能从操作系统那里挖到的最大的内存。如果添加了-Xmx参数，将以这个参数后面的值为准，例如本指令下最大内存就是1000兆。

快速启动WEKA

更加快捷的运行weka，输入以下命令：
sudo touch /usr/bin/weka
sudo chmod 775 /usr/bin/weka
sudo vi /usr/bin/weka

    输入以下代码：
    #!/bin/bash
    cd $WEKAROOT 或 cd $WEKA_PATH
    java -Xmx1000M -jar weka.jar
    保存退出vim
    以后要运行weka，只要在命令行里直接键入命令 weka 就可以了。这里附上vim编辑的一些经验：

1）vi 的进入

在 shell 模式下，键入vi 及需要编辑的文件名，即可进入vi。

例如：

vi example.txt

即可编辑 example.txt 文件。如果该文件存在，则编辑界面中会显示该文件的内容，并将光标定位在文件的第一行；如果文件不存在，则编辑界面中无任何内容。如果需要在进入vi 编辑界面后，将光标置于文件的第n 行，则在vi命令后面加上+n 参数即可。例如需要从example.txt 文件的第5 行开始显示，则使用如下命令：

vi +5 example.txt

2）退出 vi

退出 vi 时，需要在末行模式中输入退出命令q。

如果在文本输入模式下，首先按ESC 键进入命令模式，然后输入": "进入末行模式。在末行模式下，可使用如下退出命令：

:q 直接退出如果在文本输入模式下修改了文档内容则不能退出

:wq 保存后退出

:x 同 wq

:q! 不保存内容强制退出

（二）WEKA在Windows下的配置

安装WEKA的EXE程序包

下载weka在Windows下的可执行包

官方网站提供两类Windows下的可执行包，一类是OS直接运行的，另一类是在JVM里运行的，我下载的是基于JVM运行的类型的可执行包。

安装过程没有什么可说的，Windows下的安装过程非常简单易懂。

运行WEKA

运行Weka

运行Weka有两类方式，一类是通过OS的操作方式运行，如双击运行或调用exe等等。还有一类是通过Java命令运行。

OS操作下运行Weka感觉上是没有什么问题，注意是"感觉上"没有问题！事实上通过OS运行，由于什么错误也没有，可能发觉不到Weka的一些Warning。直到你需要某项Weka读取数据库的功能操作时，才发现怎么也运行不通，而却不知道为什么。

在调用Java命令运行的过程中就发现，几个关于数据库读取的Warning！处理需要一定时间。相关Warning如下：

>java –Xmx1024M –jar weka.jar

Trying to add database driver (JDBC): RmiJdbc.RJDriver - Error, not in CLASSPATH?

Trying to add database driver (JDBC): jdbc.idbDriver - Error, not in CLASSPATH?

Trying to add database driver (JDBC): org.gjt.mm.mysql.Driver - Error, not in CLASSPATH?

Trying to add database driver (JDBC): com.mckoi.JDBCDriver - Error, not in CLASSPATH?

Trying to add database driver (JDBC): org.hsqldb.jdbcDriver - Error, not in CLASSPATH?

WEKA启动的驱动报错

弥补数据库连接的问题方法（Ubuntu和Windows皆出现）

查询网络论坛，说linux和windows均会出现此类问题，我在Ubunntu和Win8都配置过了，确实都会出现这些Warning。

查询网络论坛的一些大神的实验记录与心得，两大OS的解决办法基本相同，先说说Ubuntu

1）Ubuntu解决方法

第一步、下载相关数据驱动包，大约有5个jar包，注意Weka3-6对应的这5个jar包版本各自不同，一定要找对版本的这5个jar包。例如：对于Weka(version 3.5.5) 对于RmiJdbc，一定选择版本3.05或2.5。

名字分别为：hsqldb.jar，idb.jar，mkjdbc.jar，mysql-connector-java-5.1.6-bin.jar，RmiJdbc.jar。

我的Weka版本为3-6-11，使用3-6-8版本的此5个jar包，没有问题。

第二步、解压后把这5个jar包拷贝到/usr/lib/jvm/jdk1.7.0_25 /jre/lib/ext目录下，你的路径可能和我的不一样，记着是你的jdk安装路径就行了。（吐个槽，在这一点上，Ubuntu比Windows好使多了，复制一下这几个jar包就行了，就不会报错了。可是Windows你懂的，修改环境变量起来好累。）

第三步、修改weka数据类型和数据库数据类型的映射。

（对于这步骤操作，Weka官方wiki提供相关文档操作方法http://weka.wikispaces.com/Properties+file）

在weka.jar里面有一个文件/weka/experiment/DatabaseUtils.props，记录了数据库操作的相关参数。还有很多文件DatabaseUtils.props.msaccess，DatabaseUtils.props.mssqlserver等，分别对应了各个数据库的操作参数，

如果你使用msaccess，可以把DatabaseUtils.props.msaccess的内容覆盖DatabaseUtils.props。

如果不对DatabaseUtils.props修改，可能在连接数据库时一切顺利，但在将数据装入准备预处理时，却出现找不到数据类型(can not read from database,unknown data type)之类错误。

没关系，在DatabaseUtils.props加入类型映射就OK了。文件中一般有下面的内容（这里是我用mysql对应的文件覆盖了）：

# JDBC driver (comma-separated list)

jdbcDriver=com.mysql.jdbc.Driver

# database URL

jdbcURL=jdbc:mysql://server_name:3306/database_name

# specific data types

string, getString() = 0; --> nominal

boolean, getBoolean() = 1; --> nominal

double, getDouble() = 2; --> numeric

byte, getByte() = 3; --> numeric

short, getByte()= 4; --> numeric

int, getInteger() = 5; --> numeric

long, getLong() = 6; --> numeric

float, getFloat() = 7; --> numeric

date, getDate() = 8; --> date

text, getString() = 9; --> string

time, getTime() = 10; --> date

BigDecimal,getBigDecimal()=11; -->nominal

#mysql-conversion

CHAR=0

TEXT=0

#mysql-conversion下提供的类型一般是不够的，比如int unsigned就找不到，

所以要加入int是如何映射到weka类型的。

在# specific data types下找到Int对应的java类型，这里是

int, getInteger() = 5; --> numeric

所以在#mysql-conversion下新增INT=5

再加上UNSIGNED类型，INT_UNSIGNED=6（因为unsigned比signed多一倍的数，为防止截断，要取大的类型）

其他类型的映射依次类推。

注意INT和UNSIGNED之间的下划线，缺了的话错误解决不了，我就在这里搞了好久。（Note: in case database types have blanks, one needs to replace those blanks with an underscore, e.g., DOUBLE PRECISION must be listed like this:DOUBLE_PRECISION=2. Notes from http://weka.wikispaces.com/weka_experiment_DatabaseUtils.props#toc4）

第四步，最后最重要的是，把DatabaseUtils.props放到home目录下,重启Weka后生效。并请注意：不同的数据库，书写方法与格式不同，上面是MySql类型，还有SQL Server2000或Oracle等等，格式是不同的，可百度参考相关格式或论坛博客。

2）Windows解决方法

对于找不到jdbc驱动的问题，主要是修改RunWeka.ini，因为屡次修改classpath都不成功。干脆将jar文件的地址加到weka指定的运行时classpath中。RunWeka.ini的位置在Weka总目录下，与Weka.jar是平行目录。打开后内容底部有如下内容：

# The classpath placeholder. Add any environment variables or jars to it that

# you need for your Weka environment.

# Example with an enviroment variable (e.g., THIRD_PARTY_LIBS):

# cp=%CLASSPATH%;%THIRD_PARTY_LIBS%

# Example with an extra jar (located at D:\libraries\libsvm.jar):

# cp=%CLASSPATH%;D:\\\\libraries\\\\libsvm.jar

# Or in order to avoid quadrupled backslashes, you can also use slashes "/":

# cp=%CLASSPATH%;D:/libraries/libsvm.jar

cp=%CLASSPATH%

根据提示，将jdbc驱动jar文件地址附加到cp变量。

比如mysql jdbc驱动(mysql-connector.jar)在E:/jars/下，则加入下面这句：

cp=%CLASSPATH%;E:/jars/mysql-connector.jar

同时把cp=%CLASSPATH%注释掉，

结果像

cp=%CLASSPATH%;E:/jars/mysql-connector.jar

#cp=%CLASSPATH%

也就是说如果有5个jar包，需要在一行里一个一个写进，而不能用写一个5个jar包所在的总目录来省事。（网上有人说把那5个Jar包解压到weka路径下，然后修改CLASSPATH也能解决，我试过很多次，都不可行。）

至于数据类型映射，参见上面Linux环境下的配置。

最后将DatabaseUtils.props文件放在跟Weka.jar同一目录下即可。

3）Windows下若上述方法失败，仍然报JDBC错误。

解决方法有以下几种：

一、设置系统里环境变量，因为你在RunWeka.ini内设置了classpath，结果仍然不识别，我想应该为系统里的classpath添加路径。

二、使用java命令行，利用临时权限添加classpath的方法

上面两方法，第一种我试了很多遍没有成功，第二种java命令会有问题，但最终成功。

第二种方法方法细节：

一、使用如下命令格式，但是中途出现一些问题

java -classpath E:/Weka-3-6/jars/RmiJdbc.jar -jar weka.jar

依然报5个错误，如下图。

查询相关知识，java的此classpath命令会被-jar屏蔽掉，意思就是说如果java命令里有-jar参数，则会自动屏蔽-classpath添加参数

二、我们尝试修改指令

java -Xbootclasspath/a:/E:/Weka-3-6/jars/Rmijdbc.jar: -jar Weka.jar

运行后发现少了一个错误，我们添加的是Rmijdbc驱动包，减少的错误恰好是RJDriverError，说明我们的目前指令成功，如果需要添加多个jar包，则在路径后面使用分号，逐步添加五个jar包。不要企图使用目录，使用目录仍然不识别。所以添加五个jar包的java指令确实很长。唯一欣慰的是，指令最后成功了，没有错误。不过请注意一点：由上述的分析我们知道它只是不报驱动错误了，以后我们使用数据库，它无法读取识别数据库的类型又是另外一码事。（下面有两张图，第一个图第一个指令是展示企图使用目录添加classpath是不正确的，第一个图第二个指令表明添加具体某一个jar包，成功减少了错误。第二个图第二个指令，一口气写了五个jar包，最后是成功的零错误，正确通过！。）

（三）WEKA使用的准备工作

WEKA数据格式中的数据属性

数据格式中的数据属性

1）二元属性（定性的）

二元属性的英文为"binary attribute"，比较好理解。可以认为它是一种特殊的标称属性，只有两个类别或状态：0或1，其中0通常表示该属性不出现，而1表示出现。二元属性又称布尔属性，如果两种状态对应于true和false的话。

2）标称属性（定性的）

标称属性的英文为"nominal attribute"，有时候感到不好理解。标称属性值既不是具有有意义的顺序，也不是定量的。每个值代表某种类别、编码或状态，因此标称属性又被看做是分类的（categorical），所以有时候看到顾客的ID或者鞋码尺寸SIZE等，总会误认为是序号属性。所以标称属性要抓住核心概念：标称只是一种分类，即标称数值的数学运算毫无意义。顾客ID有时候会是数值属性，但注意应用的时候，如果顾客ID之间的数值加减乘除没有任何意义，则我们不认为它是数值属性，认为其为标称属性更为恰当。以年龄为例，年龄之间常常涉及到加减，所以年龄总认为是数值属性，鞋码大小不太涉及到加减意义，故认为标称的。

3）数值属性（定量的）

数值属性的英文为"numericattribute"，它是定量的，它是可度量的量。抓住这个概念，也就是说它的数值是有意义的，可以参与加减乘除运算的，其值进行数学运算的结果常常是有意义的。

4）序数属性（定性的）

序数属性的英文单词为"ordinal attribute"，也是不太好理解的一个属性。但是切记序数属性可以通过数值属性离散化得到，并且序数属性往往携带一种重要意义，就是具有有意义的先后次序。以快餐店售卖可乐大小杯为例，0表示小杯，1表示中杯，2表示大杯。它们既可以认为是序数属性，也可以认为是间接的标称属性。或以顾客满意度调查为例，0是很不满意，1是不太满意，2是一般，3是满意，4是非常满意。

WEKA数据集格式属性

数据集格式问题

WEKA可识别ARFF格式，也可识别CSV电子数据表格式。虽然我们知道WEKA-Explorer对于两者格式都能够读取，但对于CSV格式与ARFF格式比较感兴趣。

1）CSV和ARFF格式

这里写出CSV的格式，以weather.csv为例，其内容如下表所示。至于其arff格式的规范，我们通过看后续部分，就发现两者实际上通过手动改写。ARFF格式实际上就是统计了CSV格式的属性分类，并加强规范。

outlook,temperature,humidity,windy,play

sunny,85,85,FALSE,no

sunny,80,90,TRUE,no

overcast,83,86,FALSE,yes

rainy,70,96,FALSE,yes

rainy,68,80,FALSE,yes

rainy,65,70,TRUE,no

overcast,64,65,TRUE,yes

sunny,72,95,FALSE,no

sunny,69,70,FALSE,yes

rainy,75,80,FALSE,yes

sunny,75,70,TRUE,yes

overcast,72,90,TRUE,yes

overcast,81,75,FALSE,yes

rainy,71,91,TRUE,no

2）两者转化

一、我们知道WEKA读取时会自动转化

二、如果需要人为干预，需要处理两个格式的内容，那么这就是比较有意思的事情了

ARFF文件是Weka默认的储存数据集文件。每个ARFF文件对应一个二维表格。表格的各行是数据集的各实例，各列是数据集的各个属性。

下面是Weka自带的"weather.arff"文件，在Weka安装目录的"data"子目录下可以找到。需要注意的是，在Windows记事本打开这个文件时，可能会因为回车符定义不一致而导致分行不正常。推荐使用UltraEdit这样的字符编辑软件察看ARFF文件的内容。

%ARFF file for the weather data with some numric features

@relation weather

@attribute outlook {sunny, overcast, rainy}

@attribute temperature real

@attribute humidity real @attribute windy {TRUE, FALSE} @attribute play {yes, no}

@data

% 14 instances

sunny,85,85,FALSE,no

sunny,80,90,TRUE,no

overcast,83,86,FALSE,yes

rainy,70,96,FALSE,yes

rainy,68,80,FALSE,yes

rainy,65,70,TRUE,no

overcast,64,65,TRUE,yes

sunny,72,95,FALSE,no

sunny,69,70,FALSE,yes

rainy,75,80,FALSE,yes

sunny,75,70,TRUE,yes

overcast,72,90,TRUE,yes

overcast,81,75,FALSE,yes

rainy,71,91,TRUE,no

识别ARFF文件的重要依据是分行，因此不能在这种文件里随意的断行。空行（或全是空格的行）将被忽略。

以"%"开始的行是注释，WEKA将忽略这些行。如果你看到的"weather.arff"文件多了或少了些"%"开始的行，是没有影响的。

除去注释后，整个ARFF文件可以分为两个部分。第一部分给出了头信息（Head information），包括了对关系的声明和对属性的声明。第二部分给出了数据信息（Data information），即数据集中给出的数据。虽然Weka也支持其他一些格式的文件，但是ARFF格式是支持的最好的。因此有必要在数据处理之前把CSV数据集的格式转换成ARFF。

将CSV转换为ARFF最迅捷的办法是使用WEKA所带的命令行工具。运行WEKA的主程序，在菜单中找到"Simple CLI"模块，它可提供命令行功能。在新窗口的最下方（上方是不能写字的）的输入框写上

java weka.core.converters.CSVLoader filename.csv > filename.arff

即可完成转换。

在WEKA 3.6中提供了一个"Arff Viewer"模块（在Tools里），我们可以用它打开一个CSV文件将进行浏览，然后另存为ARFF文件。进入"Exploer"模块，从上方的按钮中打开CSV文件然后另存为ARFF文件亦可。

Excel的XLS文件可以让多个二维表格放到不同的工作表（Sheet）中，我们只能把每个工作表存成不同的CSV文件。打开一个XLS文件并切换到需要转换的工作表，另存为CSV类型，点"确定"、"是"忽略提示即可完成操作。接下来把得到的CSV文件按照前述步骤转换为ARFF即可。

WEKA分类挖掘的评估标准

分类挖掘算法的评估性能标准

Confusion Matrix是混淆矩阵，提供的评估标准，如下表所示。

Predicted		C₁	¬ C₁	ALL
Actual	C₁	True Positives (TP)	False Negatives (FN)	P
Actual	¬ C₁	False Positives (FP)	True Negatives (TN)	N

1）TP/FN/FP/TN

对于C₁事件来说，可将其看成事件中的正面事件，或称为真事件，或称为阳事件。由于预测结果为C₁事件，既然结果为阳事件，正事件。说明实际过程可能由正到正，由负到正，都可成为真正，假正，说明预测都是正的。故TP可称为判正得正或真阳率或真正率，FP则为判负为正或假阳率或假正率。同理FN可推理成为判正得负或真阴率或真反率，TN顺理为判负得负或真阴率或假反率。

2）各评估率

准确率（识别率）

召回率（灵敏度）

精度

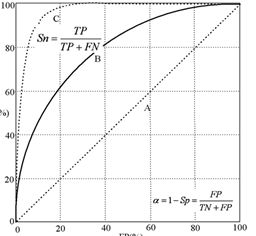
3）ROC曲线

反映的是分类器的真正例率（TPR，灵敏度）和假正例率（FPR）之间的权衡，简而言之就说观察"真判正"占据"判真"的比率。如下图所示。

WEKA软件Explorer之Classifier

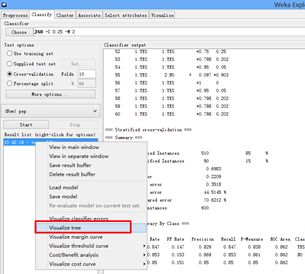
Classifier菜单面板区域模块介绍

1）Classifier

点击choose按钮，可以选择weka提供的分类器。常用的分类器有：

a）bayes下的Naïve Bayes（朴素贝叶斯）和BayesNet（贝叶斯信念网络）。

b）functions下的LibLinear、LibSVM（这两个需要安装扩展包）、Logistic Regression、Linear Regression。

c）lazy下的IB1（1-NN）和IBK（KNN）。

d）meta下的很多boosting和bagging分类器，比如AdaBoostM1。

e）trees下的J48（weka版的C4.5）、RandomForest。

2）Test options

评价模型效果的方法，有四个选项。

a）Use training set：使用训练集，即训练集和测试集使用同一份数据，一般不使用这种方法。

b）Supplied test set：设置测试集，可以使用本地文件或者url，测试文件的格式需要跟训练文件格式一致。

c）Cross-validation：交叉验证，很常见的验证方法。N-folds cross-validation是指，将训练集分为N份，使用N-1份做训练，使用1份做测试，如此循环N次，最后整体计算结果。

d）Percentage split：按照一定比例，将训练集分为两份，一份做训练，一份做测试。在这些验证方法的下面，有一个More options选项，可以设置一些模型输出，模型验证的参数。

3）Result list

这个区域保存分类实验的历史，右键点击记录，可以看到很多选项。常用的有保存或加载模型以及可视化的一些选项。

4）Classifier output

分类器的输出结果，默认的输出选项有Run information，该项给出了特征、样本及模型验证的一些概要信息；Classifier model，给出的是模型的一些参数，不同的分类器给出的信息不同。最下面是模型验证的结果，给出了一些常用的一些验证标准的结果，比如准确率（Precision），召回率（Recall），真阳性率（True positive rate），假阳性率（False positive rate），F值（F-Measure），Roc面积（Roc Area）等。混淆矩阵（Confusion Matrix）给出了测试样本的分类情况，通过它，可以很方便地看出正确分类或错误分类的某一类样本的数量。

一种旧版的WEKA软件

WEKA旧版

1）背景

为什么要用旧版？

旧版由于受众广，新版虽然新，但API的接口修改没有那么广泛。此旧版WEKA增加新版WEKA所没有的功能，受众修改的程度也较为广泛，如增加ID3可视化树的功能。此版本来自于伍斯特理工学院。软件下载网址如下：

http://davis.wpi.edu/~xmdv/weka/

2）安装

下载旧版的WEKA后，安装包的情况如下图所示。

然而直接运行RunWeka是可以成功的，界面如下：

然而有一个问题，就是点击该旧版Explorer按钮后，没有任何反应或响应。没有反应的原因，是因为没有GL4Java，如果想运行Explorer，必须安装它（旧版网址也强调了该环境）。

那么在如下网址寻找一个插件GL4Java：

http://jausoft.com/Files/Java/1.1.X/GL4Java/binpkg/

GL4Java-Installer里面有主安装程序，然而主安装程序需要一些插件辅助安装

插件的辅助清单如下图红色框内标注所示：

将辅助的插件下载并保存与旧版WEKA同一目录的文件夹内，命名为"binpkg"，文件夹内的目录结构如下图所示，binpkg文件夹内放置都是辅助插件：

然后点击GL4Java内的install.bat，就可以正常安装了，安装界面如下：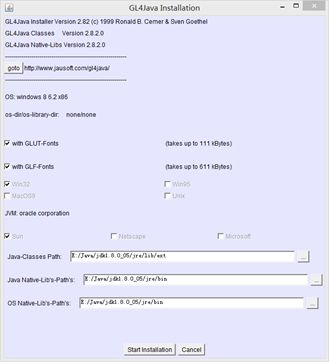

切记选中自己安装JDK的位置，然后点击Start即可。

注意：RunWeka.bat和install.bat的点击时不要以管理员身份运行，一旦以管理员身份运行，反而控制台出不来，所以直接双击就好。

3）测试

在打开旧版的WEKA后，点击Explorer，可以出现Explorer界面。

参看分类器挖掘时，我们在使用ID3分类时，可视化树的按钮是灰色的。而使用旧版WEKA后，可以看到可视化树的按钮是可以点击的。如下图所示。

（四）WEKA实验1：分类挖掘

决策树分类挖掘

实验目的

利用weka提供的决策树算法，对提供的bank-data.csv数据进行决策树分类挖掘。作业需完成以下内容：

（1）了解weka提供的数据预处理功能，去除bank-data数据中的无用属性（如ID）结构，并对income属性进行离散化处理；

（2）利用weka提供的多个决策树归纳算法，构建决策树模型（最后一个属性pep作为需要预测的属性），比较不同算法所构建模型的差别；

（3）对各种决策胡算法的预测结果进行分析，并比较分类性能。

实验过程

1）数据预处理

a）数据读取

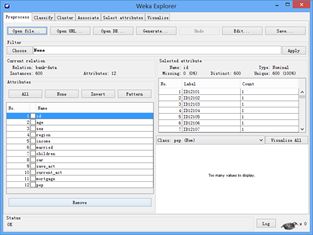
读取bank-data.csv格式数据，如下图所示。

其中bank-data数据内容呈现出来，如下图所示。

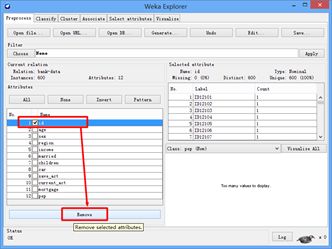
b）删除无用参数

删除无用参数ID，如下图所示。

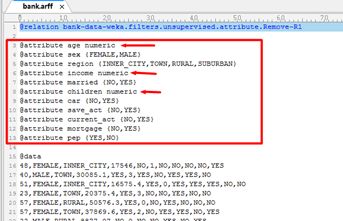
另存为ARFF格式，并用UltraEdit打开，观察数据格式，如下图所示。

根据ARFF数据格式，展示该数据的属性如下。

@attribute age numeric

@attribute sex {FEMALE,MALE}

@attribute region {INNER_CITY,TOWN,RURAL,SUBURBAN}

@attribute income numeric

@attribute married {NO,YES}

@attribute children numeric

@attribute car {NO,YES}

@attribute save_act {NO,YES}

@attribute current_act {NO,YES}

@attribute mortgage {NO,YES}

@attribute pep {YES,NO}

其中{YES,NO}是二元属性，{INNER_CITY,TOWN,RURAL,SUBURBAN}是标称属性，至于{FEMALE,MALE}是标称属性或二元属性，而numeric认为是数值属性。

说句实话，这些属性初学时基本分不清，还要对照课件才能分清楚，甚至有时对照课件都会分不清楚。所以觉得不能脱离英文环境，必须要结合英文，加强理解。可参见WEKA的数据准备里相关知识。

c）修改部分参数的数据属性

我们做一些简单修改，通过观察WEKA中某一参数的分布，如children个数，如下图所示。

children的取值分布为离散，WEKA软件显示children的Type是Numeric。我们观察直方图，children取值为0，1，2，3中的一个。我们修改ARFF格式数据，将

@attribute children numeric

修改为（请注意区分全角半角的符号）

@attribute children {0,1,2,3}

重新使用WEKA读入，再点击children参数，发现其Type更改为Nominal。如下图所示。

这说明了一点，那就是标称属性与数值属性在应用时可能没有明显的界限，只要数据属性服务于我们的要求就行。

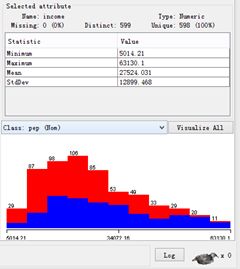
d）离散化income参数

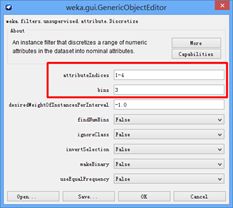
选中income，然后选择Filter-unsupervised-attribute-Discretize，然后进行后续操作，如下图所示。

修改income的离散化参数，双击choose按钮旁的命令栏，弹出weka.gui.GenericObjectEditor对话框，最上方两行分别是取值区间，分成几类。修改的参数如下图所示。

点击OK，再在命令栏右边的按钮，为保证对照对比income的分类情况，我们先观察不应用离散处理之前的情形，如下图所示。

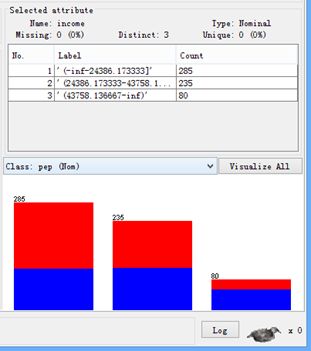
点击Apply，对income应用离散化后的生成数据情形，如下图所示，显然将income参数分成了三部分。

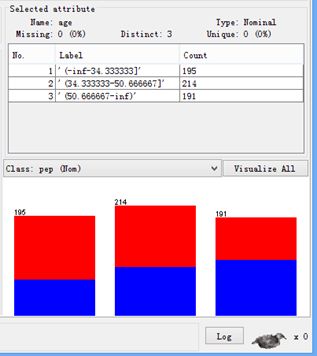
我们发现一个有趣的事实，那就是age参数也被分成了三份，如下图所示。

我猜测可能是因为在属性里面，由于我们刚刚修改了children，仅剩下age和income两个参数没有改动，且仍然保持numeric类型，应用离散化时，结果把这两个都分成了三类。说明有两个操作无效：一是只要符合离散化条件的，weka都做离散化，不管你选不选中income；二是对已有标称数值的属性作离散化处理是无效的。

2）各分类挖掘算法

a）J48分类器

打开classifier，点击choose，在分类算法中选择trees-J48，如下图所示。

选择完J48分类器后，返回到classifier界面，在TestOptions内勾选交叉验证（Cross-validation），旁边的默认值10指的是十折交叉验证。在MoreOptions中勾选Output predictions。参数设置如下图所示。

点击Start，启动实验，在右侧的classifier ouput内我们可以看到J48分类器的分类实验结果。如下图所示。

3）各分类器结果分析

a）J48分类器

先给出一些文字或数字的结果

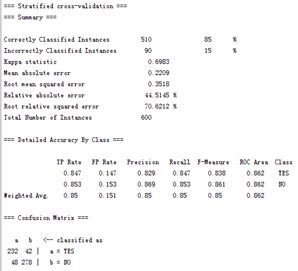
本分类器的分类验证结果，如下图所示。

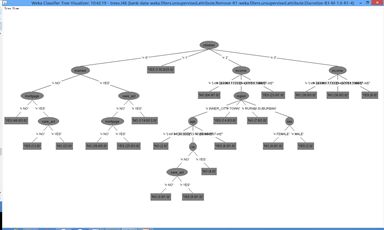
通过右键点击实验记录时间点，选择点击Visualize Tree，可以生成可视化生成树，点击操作如下图所示。

由下图可知，这是预测结果的数据，可以看到每个样本的实际分类，预测分类，预测概率以及是否错分等信息。

其中我们将分类结果文字清晰地呈现出来，进行分析。如下表所示。

=== Stratified cross-validation ===

=== Summary ===

Correctly Classified Instances 510 85%

Incorrectly Classified Instances 90 15%

Kappa statistic 0.6983

Mean absolute error 0.2209

Root mean squared error 0.3518

Relative absolute error 44.5145%

Root relative squared error 70.6212%

Total Number of Instances 600

=== Detailed Accuracy By Class ===

TP Rate FP Rate Precision Recall F-Measure ROC Area Class

0.847 0.147 0.829 0.847 0.838 0.862 YES

0.853 0.153 0.869 0.853 0.861 0.862 NO

Weighted Avg. 0.85 0.151 0.85 0.85 0.85 0.862

=== Confusion Matrix ===

a b <-- classified as

232 42 | a = YES

48 278 | b = NO

可视化结果

生成的可视化树，由于节点或分类参数较多，部分节点无法看清，但总体脉络可以如下图所示。

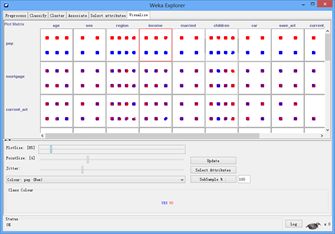
Explorer的Visualize面板，可以观察两两特征之间的样本点分布情形，如下图所示。

随便选一个区域，例如选择pep和age交叉对应的区域，点击后会出现新的图框，以展示pep特征与age特征之间的关系。如下图所示。

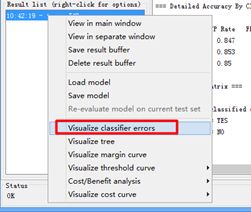
回归到Classifier面板下的ResultLists右键选择实验记录点，然后选择点击Visualize Classify Errors，如下图所示。

选择Visualize Classify Errors此项参数，然后会生成可视化结果，这个结果实际上对应的是可视化的混淆矩阵图示，也就是可以展示误判概率点（正判反，反判正），正确判别概率点（正判正，反判反），图像中十字点表示对判，方形点表示误判，X轴表示实际类别，Y轴表示预测类别。如下图所示。把鼠标放到点上，点击后也能跳出特征点的具体值，方便观察和研究特征点离群原因或不符合正常结论的原因。

同理我们再选取读取Visualize threshold curve参数，选择YES（正类），如下图所示。

Visualize threshold curve参数显示的是分类置信度在不同阈值下，分类效果评价标准的对比情况，其中就包括ROC曲线（纵轴为TP，横轴为FP），如下图所示。

b）ID3分类器

先给出一些文字或数字的结果

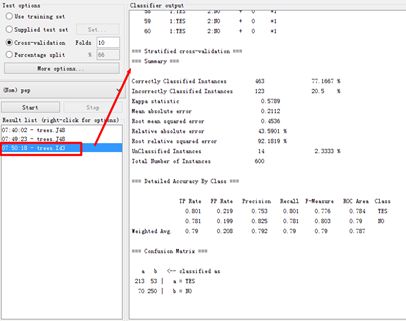
下面给出ID3的分类文字结果。

=== Stratified cross-validation ===

=== Summary ===

Correctly Classified Instances 463 77.1667 %

Incorrectly Classified Instances 123 20.5 %

Kappa statistic 0.5789

Mean absolute error 0.2112

Root mean squared error 0.4536

Relative absolute error 43.5901 %

Root relative squared error 92.1819 %

UnClassified Instances 14 2.3333 %

Total Number of Instances 600

=== Detailed Accuracy By Class ===

TP Rate FP Rate Precision Recall F-Measure ROC Area Class

0.801 0.219 0.753 0.801 0.776 0.784 YES

0.781 0.199 0.825 0.781 0.803 0.79 NO

Weighted Avg. 0.79 0.208 0.792 0.79 0.79 0.787

=== Confusion Matrix ===

a b <-- classified as

213 53 | a = YES

70 250 | b = NO

下面给出ID3的分类结果的图片示意。

可视化结果

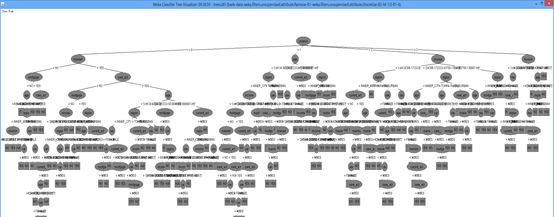
生成的可视化树步骤中发现无法生成ID3分类器，说明WEKA原版软件没有提供ID3的可视化树，故我使用了旧版WEKA，得到了相关的可视化树。

（图片这么长的原因，一是分类树有些宽大，二是我对笔记本电脑使用了扩展屏幕截屏所致。）

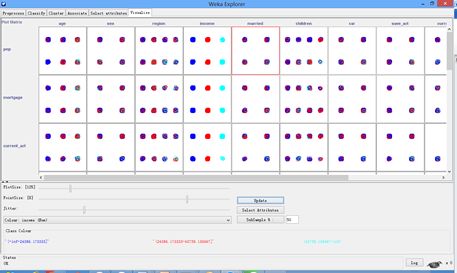
至于特征之间的关系，如下图所示。

我们选择Age和Income之间的关系进行分析，如下图所示。可以观察到年龄越小，收入越高的样本基本不存在，密集程度较高的是年龄又小收入又少的情形。

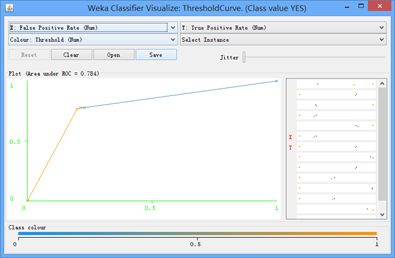
其ROC曲线可以如图所示：

c）NBTree分类器

先给出一些文字或数字的结果

NBTree是Naive Bayesian分类树，下面给出分类文字结果。

=== Stratified cross-validation ===

=== Summary ===

Correctly Classified Instances 502 83.6667 %

Incorrectly Classified Instances 98 16.3333 %

Kappa statistic 0.6697

Mean absolute error 0.2165

Root mean squared error 0.3592

Relative absolute error 43.6251 %

Root relative squared error 72.1096 %

Total Number of Instances 600

=== Detailed Accuracy By Class ===

TP Rate FP Rate Precision Recall F-Measure ROC Area Class

0.799 0.132 0.836 0.799 0.817 0.879 YES

0.868 0.201 0.837 0.868 0.852 0.879 NO

Weighted Avg. 0.837 0.169 0.837 0.837 0.836 0.879

=== Confusion Matrix ===

a b <-- classified as

219 55 | a = YES

43 283 | b = NO

在运行状态中，出现明显的停滞和计算停留，说明该分类树收敛慢，计算速度中等，占用一定时间，没有J48分类快速。

可视化结果

在这里我们简单展示NBTree的可视化树

其ROC曲线可以如下所示：

d）分析

由于篇幅过长，这里不再列举其他几类分类树的全部过程。我还测试了随机树Random Tree等等其他分类器的分类效果，测试状态如图所示。

在上述三种方法中，由数据分析我可以看到J48的分类效果最好，达到85%，其次是贝叶斯分类，达到83.7%，最差是ID3分类仅有77.1%。

而在WEKA提供的所有方法中，面对bank数据下，我将所有分类器的结果列举成表，以供阅览：

Method Name	Correctly	InCorrectly	TP/FN/FP/TN	BuildModelTIme
J48Graft	85.0000 %	15.0000 %	232/42/48/278	0.05 sec
J48	85.0000 %	15.0000 %	232/42/48/278	0.18 sec
LMT	84.1667 %	15.8333 %	222/52/43/283	16.19 sec
NBTree	83.6667 %	16.3333 %	219/55/43/283	7.3 sec
REPTree	83.5000 %	16.5000 %	229/45/54/272	0.02 sec
SimpleCart	82.3333 %	17.6667 %	213/61/45/281	2.04 sec
LADTree	81.5000 %	18.5000 %	201/73/38/288	0.47 sec
ADTree	80.5000 %	19.5000 %	192/82/35/291	0.19 sec
BFTree	80.3333 %	19.6667 %	217/57/61/265	2.07 sec
RandomForest	79.8333 %	20.1667 %	218/56/65/261	0.04 sec
ID3	77.1667 %	20.5000 %	213/53/70/250	0.13 sec
RandomTree	74.8333 %	25.1667 %	200/74/77/249	0.07 sec
FT	72.5000 %	27.5000 %	190/84/81/245	2.33 sec
DecisionStump	68.5000 %	31.5000 %	110/164/25/301	0.00 sec

解释部分算法：DecisionStump是单层决策树算法，常被作为boosting的基本学习器。LMT是组合树结构和Logistic回归模型，每个叶子节点是一个Logistic回归模型，准确性比单独的决策树和Logistic回归方法要好。NBTree是贝叶斯分类法。ADTree是一种基于boosting的决策树学习算法,其预测准确率比一般决策树高，并可以给出预测置信度，实际中常使用它的改良BICA算法。

由观察可知，J48的分类性能最好。时间收敛快，分类准确。除REPTree外，其余识别率达到80%以上的算法，收敛时间均比J48要长，分类准确性略逊一筹。值得敬佩J48的继承性与改进性，也向ID3致以敬意，没有ID3的优点，C4.5也不会继承，C4.5的信息增益率和剪枝策略是加强收敛与提高准确的重要手段。

垃圾邮件过滤

实验目的

利用weka提供的文本分类器实现英文垃圾邮件的过滤，需要完成内容如下：

（1）了解垃圾邮件过滤基本思想；

（2）利用weka的预处理功能将文本转化为向量；

（3）利用weka提供的分类算法实现垃圾邮件的过滤，最少使用两种分类器；

（4）分析分类结果，并对分类器的性能进行比较。实验过程

小知识：1978年5月3日，星期六。网络时代第一批垃圾邮件，由美国DEC公司通过互联网的前身阿帕网发送给了393个接收者。垃圾邮件，指的是不请自来、强行塞入信箱的邮件。在若干年前，邮箱存储空间普遍很小，垃圾邮件能够塞爆邮箱，让人们无法工作。

实验过程

简要分析垃圾邮件过滤的实验过程。我的初步思路是将语料库转化为向量，然后分析向量模式，过滤敏感词。最后得到垃圾样本的分类。那么这样文绉绉的话如何实践是个问题，可以说完全不知道。通过查阅互联网，明白其中含义。

语料库转化为向量，无非是将语料库的文字转化为arff格式的可读文本，并且要将文本分词处理，去标点处理等等，否则不能读入WEKA进行后续过滤。

分析向量模式，无非是用WEKA分类器去做分析。

1）数据预处理

a）文本数据读入

我们既可以自己使用Java编程或Python编程，将语料库转换为Arff格式，并做相关处理。也可以使用WEKA的接口，其提供了文本处理的一条龙服务，堪称业内楷模。

其命令行接口在Simple CLI按钮弹出的界面内，如下图所示：

我们使用WEKA的两类功能

TextDirectoryLoader

StringToWordVector

上者具有的功能为将文本转换为ARFF格式，下者具有的功能为将文本分词，去标点处理等。

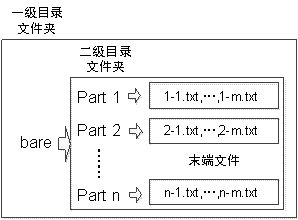
首先将文本语料以如下目录结构放置，否则WEKA命令行处理失败：

其次,值得一提bare是老师所给语料库的文件名，以及二级目录与末端文件都是老师所给的文件名，也可以根据自己需要随意重命名，只要目录关系正确就行。我的语料库全部放在test文件夹内，所以我的执行命令语句如下，并如图所示：

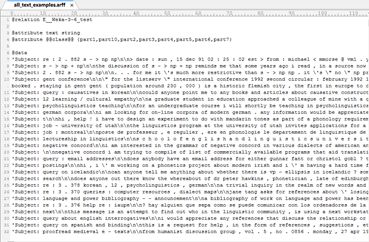
java weka.core.converters.TextDirectoryLoader -dir test > all_text_examples.arff

我们可以打开此生成ARFF文件，内容如下图所示：

观察可知，WEKA将文本语料库读入后，将每个Part的文件夹内的所有文本归为每一类class。每一类的class内的文本有多个，接下来我们要对每个class内的每将文本作切割处理分词。

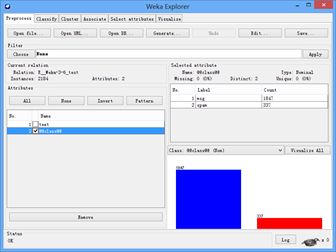
接下来，使用WEKA读入文本数据，每个文件夹内的文本数量状态可以如下图所示：

b）注意事项，避免歧途

上面a)文本数据读入，观察其中的图片，可以看到文本读入后的类有part1至part7。请注意，这样的part个数是不对的！这并不是说目录结构不对，而是说文本过滤训练的模型建模的不对！

既然要训练模型分为"不是垃圾邮件(NO)"和"是垃圾邮件(YES)"，那么我们的训练集当然在训练之处，就仅分为两个类别才对。即把垃圾邮件的文本整合在一个文件夹内，不是垃圾邮件的文本整合在另一个文件夹内，总共才两个文件夹，而不是之前part1至part7的七个文件夹。

只有分成两个文件夹去训练，这才是正确的分类结果。如果是part1至part7这样的设置，到最后训练出来的模型效果非常差。指标Relative absolute error大约高达98%，说明根本就没有分类。所以在训练集上，务必就分成两个类，一个类全是正常邮件，另一个类全是垃圾邮件。如下图所示：

c）文本向量化操作

然后选择Filter内unsupervised-attribute-StringToWordVector方法，操作如图所示：

这里简要介绍一下StringToWordVector可能需要自己做调整的参数：

-W 需要保留的单词个数，默认为1000。这不是最终的特征维数，但是维数跟此参数是正相关的

-stopwords <file> 输入停词文件，文件格式为每一个词一行。在读文件到转化特征时会自动去掉这些常用词，系统自带有一套停用词。

-tokenizer <spec> 自定义所要去除的符号，一般为标点符号。默认有常用的标点符号，但往往是不够的，所以需自己添加

其他参数只需默认值即可，可以按照图中红框的显示值修改好，可如图所示修改。

在GUI当中，还有一些参数设置需要介绍：lowerCaseTokens是否区分大小写，默认为false不区分，这里一般要设置为ture，因为同一个词就会有大小写的区别。至此文本便被分离成向量化格式。正确的向量化文本应当如下图所示：

我们注意到文本向量化的结构大致为如下，下面使用伪代码进行示意向量化文本的内容：

@attribute @@class@@ {msg,spam}

@attribute WORD1 numeric

@attribute WORD2 numeric

@attribute WORD3 numeric

@attribute WORD4 numeric

{1 0.693147,2 1.098612,4 1.386294,……,}

{4 2.70805 ,7 1.098612,8 2.639057,……,}

{0 spam,8 4.672829,9 1.791759,13 1.791759,……,}

{0 spam,2 3.218876,4 1.386294,8 2.397895,……,}

这里class的标签放在第一列。spam代表垃圾邮件，而没有标出标签的代表正常邮件，即msg。为什么spam标记出来而msg没有，这说明WEKA的命令一脉相承，即使没有出现msg标签，也可以继续投入使用。

2）垃圾邮件分类训练

a）IBk懒惰分类器

懒惰分类器顾名思义，该算法不需要太操心，投入即可使用，参数使用起来方便，参数设定不需要太专业，自然效果一般。IBk本质上就是距离为k的k最近邻分类器。IB1显然就是距离为1的k近邻分类，距离为1说明只有一个邻居，也就是说IB1总共分成两个类。选择IBk该分类器的流程如下图所示：

由于该垃圾邮件的结论具有二值性，要么是垃圾邮件，要么不是垃圾邮件。故在kNN个数上设置为1，也就是说总共分成两个类进行训练。交叉验证设为三份，便于训练快速。如下图所示：

于是，最后一步，切记将分析对象调整至class标签，否则分类不正确。调整对象的操作流程可下图所示。

最后，我们的图片结果如下：

文字结果摘录如下：

=== Stratified cross-validation ===

=== Summary ===

Correctly Classified Instances 1942 88.9194 %

Incorrectly Classified Instances 242 11.0806 %

Kappa statistic 0.5221

Mean absolute error 0.1113

Root mean squared error 0.3326

Relative absolute error 42.6065 %

Root relative squared error 92.0846 %

Total Number of Instances 2184

=== Detailed Accuracy By Class ===

TP Rate FP Rate Precision Recall F-Measure ROC Area Class

0.959 0.496 0.914 0.959 0.936 0.733 msg

0.504 0.041 0.694 0.504 0.584 0.733 spam

Weighted Avg. 0.889 0.425 0.88 0.889 0.882 0.733

=== Confusion Matrix ===

a b <-- classified as

1772 75 | a = msg

167 170 | b = spam

观察分类效果，正确分类达到88.9%，这个结果较为不错，可以接受，可以认为分类训练较为合理。观察精度precision可知，平均为88%，查全率大约为89%。总体效果良好。

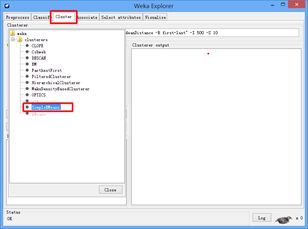
b）聚类分析之SimpleKMeans

我们使用聚类来做一次分析，请注意垃圾的过滤模型需要分类挖掘，而不是聚类。这里做聚类仅仅是观察样本的区分程度。

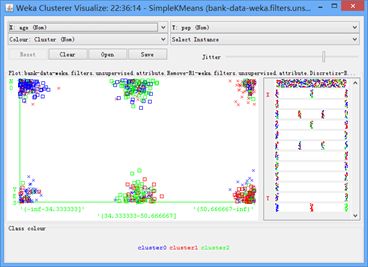
选择SimpleKMeans聚类，将聚类簇数设为两个，并将聚类分析对象设定为class标签，最后生成结果如下：

文字结果大致如下：

Number of iterations: 11

Within cluster sum of squared errors: 43032.64174958714

=== Model and evaluation on training set ===

Clustered Instances

0 464 ( 21%)

1 1720 ( 79%)

Class attribute: @@class@@

Classes to Clusters:

0 1 <-- assigned to cluster

388 1459 | msg

76 261 | spam

Cluster 0 <-- spam

Cluster 1 <-- msg

Incorrectly clustered instances : 649.0 29.7161 %

由此观察可知，迭代11次后聚成两类，聚类失败的样本大约为29%，即有71%的样本可以成功聚类，在这71%的可聚在一起的样本中又有其中的79%聚成1号类，其中的21%聚成0号类。

（五）WEKA实验2：聚类分析

聚类分析

实验目的

利用weka提供的k-means算法，对提供的bank-data.csv数据进行决策树分类挖掘。作业需完成以下内容：

（1）了解weka提供的数据预处理功能，去除bank-data数据中的无用属性（如ID）结构，并对income属性进行离散化处理；

（2）利用weka提供的k-means算法，进行聚类分析，k选不同取值，查看并比较聚类结果；

（3）选择不同的距离函数，重新进行聚类分析，并比较聚类结果。

1）数据预处理

数据预处理工作和之前在分类挖掘相似。

2）K-Means聚类算法

a）选择Cluster

我们对bank数据作聚类分析，选择K-Means算法。操作选项如图所示：

b）设置聚类参数

选择完毕后，需要对K-Means聚类设置相关参数，主要的设置区域如图所示：

显然参数设置的不同，为聚类带来的效果也不同。

主要的参数为NumCluster和Seed。

前者为聚类簇数，后者为种子数。

c）聚成2类的结果

设置聚成2类之后，生成结果如下：

文字结果大致摘录如下：

Number of iterations: 3

Within cluster sum of squared errors: 1737.4061909284878

Time taken to build model (full training data) : 0.24 seconds

=== Model and evaluation on training set ===

Clustered Instances

0 252 ( 42%)

1 348 ( 58%)

Class attribute: pep

Classes to Clusters:

0 1 <-- assigned to cluster

121 153 | YES

131 195 | NO

Cluster 0 <-- YES

Cluster 1 <-- NO

Incorrectly clustered instances : 284.0 47.3333 %

d）聚成3类的结果

假设我们将簇数取为3，随机数为10。生成结果如下：

以及主要指标结果：

可以观察其可视化结果，如图所示：

展示年龄与pep的关系

展示收入与pep的关系

展示地域与pep的关系

由上述几幅图我们可以看出聚类效果并不好，在簇点下聚类点颜色混杂度较高，区分度不好，辨析度不强，不能有效挖掘关系。其重要判定指标文字结果如下：

Class attribute: pep

Classes to Clusters:

0 1 2 <-- assigned to cluster

114 90 70 | YES

125 125 76 | NO

Cluster 0 <-- YES

Cluster 1 <-- NO

Cluster 2 <-- No class

Incorrectly clustered instances : 361.0 60.1667 %

e）调整参数

调整参数及生成结果如下

参数	NumCluster	Seed	squared errors	Incorrectly instances
2	2	10	1737.4	284.0 47.3333 %
	2	20	1723.0	294.0 49 %
	2	30	1778.3	261.0 43.5 %
	2	40	1752.7	272.0 45.3333 %
	2	50	1756.1	259.0 43.1667 %
	2	100	1773.0	271.0 45.1667 %
3	3	10	2143.0	361.0 60.1667 %
	3	20	2121.0	378.0 63 %
	3	30	2168.0	340.0 56.6667 %
	3	40	2166.0	341.0 56.8333 %
	3	50	2159.0	319.0 53.1667 %
	3	100	2151.0	295.0 49.1667 %
4	4	10	1991.0	416.0 69.3333 %
	4	20	2018.0	400.0 66.6667 %
	4	30	2118.0	353.0 58.8333 %
	4	40	2071.0	393.0 65.5 %
	4	50	2069.0	336.0 56 %
	4	100	2046.0	349.0 58.1667 %
5	5	10	1916	441.0 73.5 %
	5	20	1935.0	416.0 69.3333 %
	5	30	1976.0	388.0 64.6667 %
	5	40	1925.0	426.0 71 %
	5	50	1956.0	378.0 63 %
	5	100	1971.0	374.0 62.3333 %
6	6	10	1889.0	441.0 73.5 %
	6	20	1864	414.0 69 %
	6	30	1899.0	407.0 67.8333 %
	6	40	1914.0	434.0 72.3333 %
	6	50	1887.0	396.0 66 %
	6	100	1864.0	401.0 66.8333 %
7	7	10	1805.0	472.0 78.6667 %
	7	20	1832	419.0 69.8333 %
	7	30	1854.0	411.0 68.5 %
	7	40	1831.0	453.0 75.5 %
	7	50	1805.0	414.0 69 %
	7	100	1813.0	416.0 69.3333 %
8	8	10	1807.0	473.0 78.8333 %
	8	20	1733	445.0 74.1667 %
	8	30	1756.0	447.0 74.5 %
	8	40	1702.0	459.0 76.5 %
	8	50	1689.0	433.0 72.1667 %
	8	100	1745.0	450.0 75 %
9	9	10	1750.0	482.0 80.3333 %
	9	20	1688	454.0 75.6667 %
	9	30	1718.0	451.0 75.1667 %
	9	40	1681.0	476.0 79.3333 %
	9	50	1721.0	460.0 76.6667 %
	9	100	1657.0	465.0 77.5 %
10	10	10	1655.0	497.0 82.8333 %
	10	20	1647.0	459.0 76.5 %
	10	30	1707.0	455.0 75.8333 %
	10	40	1599.0	495.0 82.5 %
	10	50	1608	469.0 78.1667 %
	10	100	1617.0	470.0 78.3333 %

f）数据分析

在同一情况下，根据当前Within cluster sum of squared errors，调整"seed"参数，观察Within cluster sum of squared errors（SSE）变化。采纳SSE最小的一个结果。

结合实际情况，对于pep仅有YES，NO的两个结果的事实，一般聚簇调整为2个。再在2个聚簇的条件内选择合适的方差中心。

3）层次聚类

a）选择层次聚类HierarchicalCluster

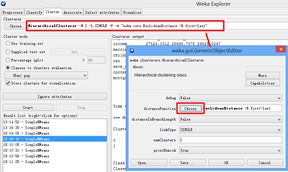
鉴于K-Means聚类的操作解释足够详细，这里有详有略地介绍实验内容。如下图展示选择聚类方法：

在如下图所示的按钮中，点击cluster的命令行栏，弹出通知，点选choose可以更换不同的距离函数。

b）层次聚类过程及结果

我们当前选择欧式距离，选择分析对象为Pep，再运行start。生成的图片结果为：

文字摘录结果如下：

Time taken to build model (full training data) : 16.32 seconds

=== Model and evaluation on training set ===

Clustered Instances

0 599 (100%)

1 1 ( 0%)

Class attribute: pep

Classes to Clusters:

0 1 <-- assigned to cluster

274 0 | YES

325 1 | NO

Cluster 0 <-- NO

Cluster 1 <-- No class

Incorrectly clustered instances : 275.0 45.8333 %

对比K-Means聚类，KMeans聚类的参数结果如下。

KMeansIncorrectly clustered instances : 284 43.3333 %

那么再看看层次聚类的结果

0 1 <-- assigned to cluster

274 0 | YES 45.7%

325 1 | NO 54.3%

对比KMeans聚类

Clustered Instances

0 252 ( 42%)

1 348 ( 58%)

为什么这么对比，为什么层次聚类的其中某一个样本单独作为一个类。原因在于层次聚类的规则算法，详情可参见书籍或互联网。层次聚类的最后一次操作，当然为大集合类与最后一个类的合并过程。故WEKA的层次聚类停留在最后一次上。在对比标签的类上，两者聚类的效果近似，没有明显分别。

c）距离函数更改为切比雪夫距离

我们更换距离函数为切比雪夫距离公式，测试结果如图所示。

文字结果摘录如下。

Time taken to build model (full training data) : 8.87 seconds

=== Model and evaluation on training set ===

Clustered Instances

0 1 ( 0%)

1 599 (100%)

Class attribute: pep

Classes to Clusters:

0 1 <-- assigned to cluster

1 273 | YES

0 326 | NO

Cluster 0 <-- YES

Cluster 1 <-- NO

Incorrectly clustered instances : 273.0 45.5 %

曼哈顿距离(Manhattan Distance)可以理解为一阶范数距离，欧式距离(Euclidean Distance)可以理解为二阶范数距离，切比雪夫距离(Chebyshev Distance)可以理解为无穷范数距离。故在更改选择距离范数的策略上，可能不具有左右影响力，原因在于距离函数的公式彼此之间相差无几。

4）K-Means与层次聚类比较

对于K-Means算法，其时间复杂度为O(tKmn)，其中，t为迭代次数，K为簇的数目，m为数据记录数，n为维数

空间复杂度为O((m+K)n)，其中，K为簇的数目，m为数据记录数，n为维数。

以实验为例，在簇数为2的情形下分析bank数据，迭代次数为3次，数据记录数大约为600条，维数为11维。时间复杂度大约为3万，空间复杂度大约为6千。

对于层次聚类算法，层次聚类的空间复杂度O(m²)。总时间复杂度O(m²logm)，其中m是数据记录数。对于本实验而言，空间复杂度大约为36万，时间复杂度上大约近乎100万。故显然在运行时间上，理论分析结果是层次聚类运行时间更长。

根据WEKA分别运行两算法的时间结果，对比可知如下：

Name	K-Means(欧氏，2类)	层次聚类
Time	0.24 sec	16.32 sec

5）文本聚类

可参见垃圾邮件过滤中德聚类分析。

（六）WEKA实验3：Apriori关联挖掘

实验目的

实验目的

利用weka提供的关联算法，实现给定数据对象的关联挖掘。

WEKA关联挖掘

1）数据预处理

首先对bank数据进行预处理，预处理的对象包括有"ID"，"income"和"children"。对于ID要remove，对于income使用离散化过滤，使其在1至4之间，形成三份。children则在文本文件中修改参数，详细操作在实验1中应该非常详细，故不再赘述。

唯有处理掉所有Numeric数据，全部转化为Nominal类型数据，才可以使用Apriori算法，否则该算法按钮为灰色不可选状态。

2）关联挖掘

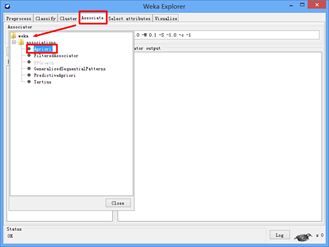
选择Apriori算法的操作如图所示。

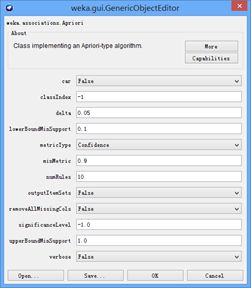
对于Apriori的参数窗口，可以点击命令行栏弹出。图片内容如图所示。

详细的参数含义如下罗列：

car 如果设为真，则会挖掘类关联规则而不是全局关联规则。

classindex 类属性索引。如果设置为-1，最后的属性被当做类属性。

delta 以此数值为迭代递减单位。不断减小支持度直至达到最小支持度或产生了满足数量要求的规则。

lowerBoundMinSupport 最小支持度下界。

metricType 度量类型。设置对规则进行排序的度量依据。可以是：置信度（类关联规则只能用置信度挖掘），提升度(lift)，杠杆率(leverage)，确信度(conviction)。

在 Weka中设置了几个类似置信度(confidence)的度量来衡量规则的关联程度，它们分别是：

a) Lift ： P(A,B)/(P(A)P(B)) Lift=1时表示A和B独立。这个数越大(>1)，越表明A和B存在于一个购物篮中不是偶然现象,有较强的关联度。

b)Leverage :P(A,B)-P(A)P(B) Leverage=0时A和B独立，Leverage越大A和B的关系越密切。

c) Conviction:P(A)P(!B)/P(A,!B) （!B表示B没有发生） Conviction也是用来衡量A和B的独立性。从它和lift的关系（对B取反，代入Lift公式后求倒数）可以看出，这个值越大, A、B越关联。

minMtric 度量的最小值。

numRules 要发现的规则数。

outputItemSets 如果设置为真，会在结果中输出项集。

removeAllMissingCols 移除全部为缺省值的列。

significanceLevel 重要程度。重要性测试（仅用于置信度）。

upperBoundMinSupport 最小支持度上界。从这个值开始迭代减小最小支持度。

verbose 如果设置为真，则算法会以冗余模式运行。

根据实际情况，我们将参数设置为：

% car I - 输出项集，若设为false则该值缺省;

% numRules N 10 - 规则数为10;

% metricType T 0 – 度量单位选为置信度，(T1-提升度，T2杠杆率，T3确信度);

% minMetric C 0.9 – 度量的最小值为0.9;

% delta D 0.05 - 递减迭代值为0.05;

% upperBoundMinSupport U 1.0 - 最小支持度上界为1.0;

% lowerBoundMinSupport M 0.5 - 最小支持度下界为0.5;

% significanceLevel S -1.0 - 重要程度为-1.0;

% classIndex c -1 - 类索引为-1输出项集设为真

% (由于car, removeAllMissingCols, verbose都保持为默认值False，因此在结果的参数设置为缺省，若设为True，则会在结果的参数设置信息中分别表示为A, R,V)

那么配置好参数，我们应用关联挖掘算法于bank数据，结果如图所示。

文字结果摘录如下：

Apriori

=======

Minimum support: 0.1 (60 instances)

Minimum metric <confidence>: 0.9

Number of cycles performed: 18

Generated sets of large itemsets:

Size of set of large itemsets L(1): 28

Size of set of large itemsets L(2): 232

Size of set of large itemsets L(3): 524

Size of set of large itemsets L(4): 277

Size of set of large itemsets L(5): 33

Best rules found:

1. income='(43758.136667-inf)' 80 ==> save_act=YES 80 conf:(1)

2. age='(50.666667-inf)' income='(43758.136667-inf)' 76 ==> save_act=YES 76 conf:(1)

3. income='(43758.136667-inf)' current_act=YES 63 ==> save_act=YES 63 conf:(1)

4. age='(50.666667-inf)' income='(43758.136667-inf)' current_act=YES 61 ==> save_act=YES 61 conf:(1)

5. children=0 save_act=YES mortgage=NO pep=NO 74 ==> married=YES 73 conf:(0.99)

6. sex=FEMALE children=0 mortgage=NO pep=NO 64 ==> married=YES 63 conf:(0.98)

7. children=0 current_act=YES mortgage=NO pep=NO 82 ==> married=YES 80 conf:(0.98)

8. children=0 mortgage=NO pep=NO 107 ==> married=YES 104 conf:(0.97)

9. income='(43758.136667-inf)' current_act=YES 63 ==> age='(50.666667-inf)' 61 conf:(0.97)

10. income='(43758.136667-inf)' save_act=YES current_act=YES 63 ==> age='(50.666667-inf)' 61 conf:(0.97)

3）调整参数

根据任务要求，调整MetricType参数，可以得到下表：

	Output
Lift	Minimum support: 0.25 (150 instances) Minimum metric <lift>: 1.1 Number of cycles performed: 15 Generated sets of large itemsets: Size of set of large itemsets L(1): 21 Size of set of large itemsets L(2): 59 Size of set of large itemsets L(3): 16 Best rules found: 1. age='(-inf-34.333333]' 195 ==> income='(-inf-24386.173333]' 174 conf:(0.89) < lift:(1.88)> lev:(0.14) [81] conv:(4.65) 2. income='(-inf-24386.173333]' 285 ==> age='(-inf-34.333333]' 174 conf:(0.61) < lift:(1.88)> lev:(0.14) [81] conv:(1.72) 3. married=YES 396 ==> mortgage=NO pep=NO 171 conf:(0.43) < lift:(1.24)> lev:(0.06) [33] conv:(1.14) 4. mortgage=NO pep=NO 209 ==> married=YES 171 conf:(0.82) < lift:(1.24)> lev:(0.06) [33] conv:(1.82) 5. married=YES mortgage=NO 261 ==> pep=NO 171 conf:(0.66) < lift:(1.21)> lev:(0.05) [29] conv:(1.31) 6. pep=NO 326 ==> married=YES mortgage=NO 171 conf:(0.52) < lift:(1.21)> lev:(0.05) [29] conv:(1.18) 7. children=0 263 ==> pep=NO 167 conf:(0.63) < lift:(1.17)> lev:(0.04) [24] conv:(1.24) 8. pep=NO 326 ==> children=0 167 conf:(0.51) < lift:(1.17)> lev:(0.04) [24] conv:(1.14) 9. married=YES save_act=YES 277 ==> pep=NO 175 conf:(0.63) < lift:(1.16)> lev:(0.04) [24] conv:(1.23) 10. pep=NO 326 ==> married=YES save_act=YES 175 conf:(0.54) < lift:(1.16)> lev:(0.04) [24] conv:(1.15)
Leverage	Minimum support: 0.1 (60 instances) Minimum metric <leverage>: 0.1 Number of cycles performed: 18 Generated sets of large itemsets: Size of set of large itemsets L(1): 28 Size of set of large itemsets L(2): 232 Size of set of large itemsets L(3): 524 Size of set of large itemsets L(4): 277 Size of set of large itemsets L(5): 33 Best rules found: 1. age='(-inf-34.333333]' 195 ==> income='(-inf-24386.173333]' 174 conf:(0.89) lift:(1.88) < lev:(0.14) [81]> conv:(4.65) 2. income='(-inf-24386.173333]' 285 ==> age='(-inf-34.333333]' 174 conf:(0.61) lift:(1.88) < lev:(0.14) [81]> conv:(1.72) 3. age='(-inf-34.333333]' 195 ==> income='(-inf-24386.173333]' current_act=YES 138 conf:(0.71) lift:(1.97) < lev:(0.11) [68]> conv:(2.16) 4. income='(-inf-24386.173333]' current_act=YES 215 ==> age='(-inf-34.333333]' 138 conf:(0.64) lift:(1.97) < lev:(0.11) [68]> conv:(1.86) 5. income='(-inf-24386.173333]' 285 ==> age='(-inf-34.333333]' current_act=YES 138 conf:(0.48) lift:(1.9) < lev:(0.11) [65]> conv:(1.43) 6. age='(-inf-34.333333]' current_act=YES 153 ==> income='(-inf-24386.173333]' 138 conf:(0.9) lift:(1.9) < lev:(0.11) [65]> conv:(5.02)
Conviction	Minimum support: 0.25 (150 instances) Minimum metric <conviction>: 1.1 Number of cycles performed: 15 Generated sets of large itemsets: Size of set of large itemsets L(1): 21 Size of set of large itemsets L(2): 59 Size of set of large itemsets L(3): 16 Best rules found: 1. age='(-inf-34.333333]' 195 ==> income='(-inf-24386.173333]' 174 conf:(0.89) lift:(1.88) lev:(0.14) [81] < conv:(4.65)> 2. mortgage=NO pep=NO 209 ==> married=YES 171 conf:(0.82) lift:(1.24) lev:(0.06) [33] < conv:(1.82)> 3. income='(-inf-24386.173333]' 285 ==> age='(-inf-34.333333]' 174 conf:(0.61) lift:(1.88) lev:(0.14) [81] < conv:(1.72)> 4. age='(50.666667-inf)' 191 ==> save_act=YES 151 conf:(0.79) lift:(1.15) lev:(0.03) [19] < conv:(1.44)> 5. save_act=YES pep=NO 235 ==> married=YES 175 conf:(0.74) lift:(1.13) lev:(0.03) [19] < conv:(1.31)> 6. married=YES mortgage=NO 261 ==> pep=NO 171 conf:(0.66) lift:(1.21) lev:(0.05) [29] < conv:(1.31)> 7. pep=NO 326 ==> married=YES 242 conf:(0.74) lift:(1.12) lev:(0.04) [26] < conv:(1.3)> 8. children=0 263 ==> pep=NO 167 conf:(0.63) lift:(1.17) lev:(0.04) [24] < conv:(1.24)> 9. married=YES save_act=YES 277 ==> pep=NO 175 conf:(0.63) lift:(1.16) lev:(0.04) [24] < conv:(1.23)> 10. current_act=YES pep=NO 244 ==> married=YES 177 conf:(0.73) lift:(1.1) lev:(0.03) [15] < conv:(1.22)>

至此关联挖掘的实验结束。

（七）WEKA实验改进：二次开发

实验目的

实验目的

（1）尝试简单的WEKA二次开发入门知识；

（2）总结网络及论坛的各类二次开发经验与技巧；

（3）实践二次开发的小实验。

WEKA二次开发的准备工作

1）WEKA二次开发的准备分析

通过咨询老师和查阅网络论坛资料，发现WEKA二次开发过程提供的教程良莠不齐。原因归结于几点：

a)WEKA版本众多，稳定版开发版尝试的人均不一样，操作的顺序流程也不尽相同。

b)WEKA的二次开发涉及到Eclipse，不同版本的操作软件集成环境也不尽相同。

c)提供的教程有时不充分，涉及到关键的部分时，总是没有详细解释，故需要摸索一条符合实际情况的道路。

2）WEKA二次开发的版本准备

通过结合网络资料，决定要么采用WEKA3-4-X的稳定版，要么采用WEKA3-6-X稳定版本，其中值得一提的是对于WEKA3-5-X网络论坛网友也有尝试，应该是成功的，但是局限在WEKA3-5版本内。二次开发的流程区别在3-4和3-5之间成为分界岭，但应当是细节的不同。历届版本的下载网址见如下：

http://sourceforge.net/projects/weka/files/weka-3-4-windows/

这里我展示WEKA3-4-10和WEKA3-6-11的二次开发环境配置。

3）WEKA3-4-10二次开发的配置

WEKA3-4-10的界面如下：

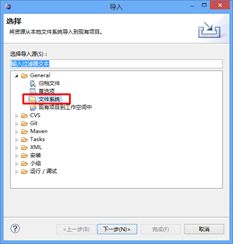
建立Eclipse的java项目工程，该过程不赘述，然后项目工程的基本目录结构要有，也就是说，得有src文件夹，链接库等。继而开始正式的步骤，右键点击weka项目名，点击导入，并选择文件系统，所选的文件系统为你weka软件目录下的weka-src文件（如果是jar包状态，请解压后导入），导入操作如图所示：

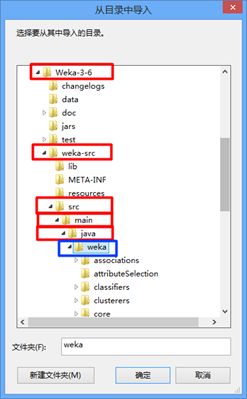
然后选择导入文件的路径，在这里请注意！非常重要的是，一定要选择正确目录。请与java程序中package的路径一致，不要跟网络论坛资料人云亦云！网络论坛教程资料有时不符合你的实际情况。

我通过举例子，下图中有带"勾"的目录，和带"叉"的目录。"勾"是正确的目录,"叉"是错误路径，而"叉"往往都是教程提供的路径，这是因为java程序中package的内容是weka.xxxxxx。那么目录一定要在weka/xxxxx下。

所以导入后，各src下的程序文件都带有weka的"头"，如下图细红框标注所示。如果设置错误的路径，则会提示error，关于无法找到package路径的问题。通过设置正确的文件目录后，基本已无error，大多出现warning，如下图粗红框内所示，这是正常现象。现在已经可以做开发编程，warning并不会影响。

4）WEKA3-6-11二次开发的配置

WEKA3-6-11导入的也是WEKA3-6-11目录下的weka-src，如果weka-src是jar包状态，请解压后导入。导入的路径选择为下图所示，其中红色框为路径节点，蓝色框是点击选择的目录路径，即鼠标点击红色框内文件夹名字，再点击确定即可：

导入后会出现无法解析类型的错误，如下图所示。

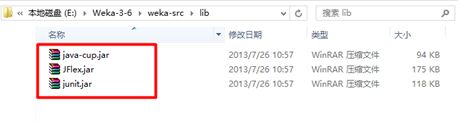
一般是缺少动态库所致，此时需要链接相关的库。链接的库jar包全部在weka-src文件夹lib目录下。可对Eclipse的JRE系统库上右键点选"构建路径-配置构建路径"，在弹出的窗口中，选择"添加外部jar"，进入刚才所说的路径，把三个jar导入。此时Eclipse左侧栏产生了"引用库"内容。

此时不再提示无法解析类型错误，但仍然有一些错误未能解决，例如"覆盖超类的错误"没有解决，此问题一般是Java编译器版本设置问题。

修改你的eclipse指定的编译器版本。在选项里的java compiler中指定版本至少在5.0以上。在myEclipse中改变编译器的方法：Project->Properties->JavaCompiler

->ConfigureWorkspace Setting，在弹出的页面中可以进行设置。

如果是Eclipse下，请在"窗口-首选项"下的弹出窗口内，操作如图：

然后点选"java-编译器"，更改一致性级别，调整至1.7，此数值对应编译5.0版本以上，可以提供兼容覆盖超类语法的编译环境。

至此，所有错误都消失，但Warning存在，仍然是不影响二次开发编程的。通过找到"weka gui"下的"guichooser.java"，点击运行，即可看见wekaGUI界面。如需要添加自己的程序，则添加新的java程序，编写符合weka接口的新程序，再通过可视化界面运行即可。

##########点击运行，即可看见wekaGUI界面。如需要添加自己的程序，则添加新的java程序，编写符合weka接口的新程序，再通过可视化界面运行即可。

WEKA二次开发小实验

1）WEKA的classpath链接开发

咨询老师和查阅互联网，教程提供各种不对，所以有一句话说得好，要走出自己的特色道路，不要迷信于别人的道路，不要迷失自己的道路，对自己的道路要自信。这句话意味着，不要认为自己完全不明白，WEKA和java eclipse实验做到这个份上，有些知识要自己去举一反三，触类旁通。以增加LibSvm的jar包为例，这里我们采用链接至系统路径中方法，使WEKA的jar包调用。

灵感在于，咨询老师时，老师建议使用支持向量机的方法去对垃圾邮件作训练。那么如果需要该方法训练，需要下载与WEKA版本对应的jar库，有两个，一个是libsvm.jar，另一个是wlsvm.jar。下载地址可以是：

http://www.cs.iastate.edu/~yasser/wlsvm/

　　下图展示的是WEKA3-4版本就没有保留LibSvm的位置，故无此项。

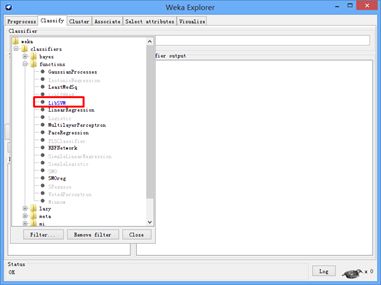
下图展示的是WEKA3-6版本，它虽然保留LibSvm的位置，但如果缺少其jar包，则显示为蓝色状态。由于我的WEKA为3-6版本，当时Classify里的Classifier-functions内Libsvm是蓝色的，即未连接状态。即使运行，也会报出错误。

所报错误如下：

这是由于没有相关库，而强行运行所致。即便下载了相关库，不进行环境变量的添加，也不行。此时不要迷信别人的方法，也不要迷信我的方法，我的方法是我根据自己的情况摸索出来的。

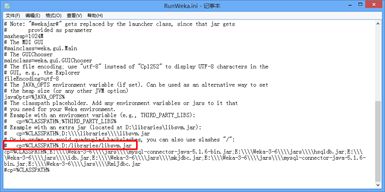
首先要配置WEKA安装目录下的文件RunWeka.ini配置文件，打开后，观察其中一句语句。显然此语句提供的了classpath的路径。（网上的修改方法完全忽略此语句，如果不注意到这个细节，则南辕北辙。这也是因为3-6版本较高不同于以前的版本的缘故，所以参考别人教程要注意自己的环境。）

然后根据该配置文件的案例，即

# cp=%CLASSPATH%;D:/libraries/libsvm.jar

我们模仿一下，在上面的这个注释下方一行，添加一条语句，类似可如下：

cp=%CLASSPATH%;E:/Weka-3-6/wlsvm.jar;E:/Weka-3-6/libsvm.jar;

请注意，上面的指令具备两个条件，一是你要把这两个相关库放在WEKA目录下，二是指令要写在注释行下方。然后保存关闭，点击RunWeka.bat去更新（记住用管理员权限打开一次，然后再双击打开一次。前者方式的打开会打不开，后者的方式会打开。个中玄妙，唯有实践者才会体会）。此时再打开WEKA-Explorer，寻找Libsvm功能时，是黑色的，可选的，可用的，如下所示：

说明此时可以运行Libsvm成功，至于运行是否成功还未可知。

我们使用Libsvm库对垃圾邮件做分类，一般来说调用Libsvm会出现两个错误：

一是，start后报错：problem evaluating classifier: rand

该问题解决方法是，更新libsvm较高，原因是libsvm的版本低。更为重要的是，WLSvm的文件包下载下来时是ZIP压缩文件，打开后里面会有libsvm，记住不要用WLSvm里的libsvm，这个libsvm不是WEKA软件里链接命名的libsvm。需要下载libsvm.zip压缩包里的文件，并引用这里面的文件。

二是，报错关于不能处理Could not handle Numeric数据

简单，把分类关键标签离散化为二值。以邮件过滤为例，class标签要么是msg代表正常邮件，要么是spam代表垃圾邮件。我们只要离散化class的值即可。我自己操作的时候把msg标为1，spam标为2。

其中离散化成为Nominal类型的图片结果如下：

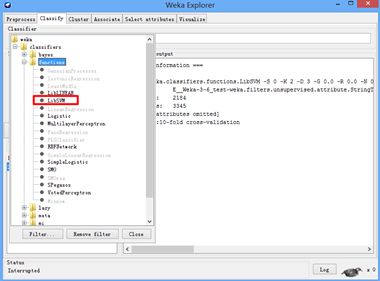
使用Libsvm生成训练结果的图片如下：

文字结果摘要如下：

=== Classifier model (full training set) ===

LibSVM wrapper, original code by Yasser EL-Manzalawy (= WLSVM)

Time taken to build model: 27.18 seconds

=== Stratified cross-validation ===

=== Summary ===

Correctly Classified Instances 1938 88.7363 %

Incorrectly Classified Instances 246 11.2637 %

Kappa statistic 0.3849

Mean absolute error 0.1126

Root mean squared error 0.3356

Relative absolute error 43.1037 %

Root relative squared error 92.9061 %

Total Number of Instances 2184

=== Detailed Accuracy By Class ===

TP Rate FP Rate Precision Recall F-Measure ROC Area Class

1 0.73 0.882 1 0.938 0.635 msg

0.27 0 1 0.27 0.425 0.635 spam

Weighted Avg. 0.887 0.617 0.901 0.887 0.859 0.635

=== Confusion Matrix ===

a b <-- classified as

1847 0 | a = msg

246 91 | b = spam

观察相关参数，知支持向量机下的精度要比K近邻懒惰算法还要好，召回率与K懒惰算法不相上下，对于正例判决是满分，即百分百，足见支持向量机果然大名鼎鼎。

后记

感谢老师的帮助，没有两位老师的课上教学和课下指导，我是根本不可能做出来的。对于WEKA的理解和HADOOP的理解又不断深入。

本科毕业的时候，我的本科导师就教导过道德经中有云"为学日益，为道日损，损之又损，以至于无为，无为而无不为。"求学日益精进，实践日益渐辛。等到一天，求学不断进步，实践不断圆满，以至于无为，无为也就无不为了，当然这也是理想的境界，也是不断追求的境界。

谢谢老师！真的是麻烦您了！

WEKA使用（基础配置+垃圾邮件过滤+聚类分析+关联挖掘）

（一）WEKA在Ubuntu下的配置

下载解压

下载和解压weka

配置Ubuntu的环境变量

运行WEKA

快速启动WEKA

1）vi 的进入

2）退出 vi

（二）WEKA在Windows下的配置

安装WEKA的EXE程序包

运行WEKA

WEKA启动的驱动报错

1）Ubuntu解决方法

2）Windows解决方法

3）Windows下若上述方法失败，仍然报JDBC错误。

（三）WEKA使用的准备工作

WEKA数据格式中的数据属性

1）二元属性（定性的）

2）标称属性（定性的）

3）数值属性（定量的）

4）序数属性（定性的）

WEKA数据集格式属性

1）CSV和ARFF格式

2）两者转化

WEKA分类挖掘的评估标准

1）TP/FN/FP/TN

2）各评估率

3）ROC曲线

WEKA软件Explorer之Classifier

1）Classifier

2）Test options

3）Result list

4）Classifier output

一种旧版的WEKA软件

1）背景

2）安装

3）测试

（四）WEKA实验1：分类挖掘

决策树分类挖掘

1）数据预处理

a）数据读取

b）删除无用参数

c）修改部分参数的数据属性

d）离散化income参数

2）各分类挖掘算法

a）J48分类器

3）各分类器结果分析

a）J48分类器

b）ID3分类器

c）NBTree分类器

d）分析

垃圾邮件过滤

1）数据预处理

a）文本数据读入

b）注意事项，避免歧途

c）文本向量化操作

2）垃圾邮件分类训练

a）IBk懒惰分类器

b）聚类分析之SimpleKMeans

（五）WEKA实验2：聚类分析

聚类分析

1）数据预处理

2）K-Means聚类算法

a）选择Cluster

b）设置聚类参数

c）聚成2类的结果

d）聚成3类的结果

e）调整参数

f）数据分析

3）层次聚类

a）选择层次聚类HierarchicalCluster

b）层次聚类过程及结果

c）距离函数更改为切比雪夫距离

4）K-Means与层次聚类比较

5）文本聚类

（六）WEKA实验3：Apriori关联挖掘

实验目的

WEKA关联挖掘

1）数据预处理