最小包围多边形（凸包；最小包围点集）——C代码例子

本文来自：http://alienryderflex.com/smallest_enclosing_polygon/

 

这个C代码例子需要一群2维点集，如下图所示：

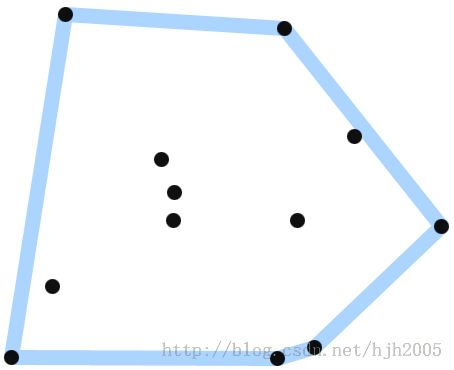
要获得包含这些点的最小多边形如下图所示：

查找点集最小多边形的一种方法是——将所有点都传到函数中计算。

这段代码没有充分的测试过，所以如果你有任何问题，请告诉我。这个函数可以应对重叠点的问题，如果角点上有重叠点，它只会返回一个点。

 

//  public-domain code by Darel Rex Finley, January 2009



#define  CIRCLE_RADIANS  6.283185307179586476925286766559



//  Determines the radian angle of the specified point (as it relates to the origin).
//
//  Warning:  Do not pass zero in both parameters, as this will cause division-by-zero.

double angleOf(double x, double y) {

  double  dist=sqrt(x*x+y*y) ;

  if (y>=0.) return acos( x/dist)                  ;
  else       return acos(-x/dist)+.5*CIRCLE_RADIANS; }



//  Pass in a set of 2D points in x,y,points.  Returns a polygon in polyX,polyY,polyCorners.
//
//  To be safe, polyX and polyY should have enough space to store all the points passed in x,y,points.

void findSmallestPolygon(double *x, double *y, long points, double *polyX, double *polyY, long *polyCorners) {

  double  newX=x[0], newY=y[0], xDif, yDif, oldAngle=.5*CIRCLE_RADIANS, newAngle, angleDif, minAngleDif ;
  long    i ;

  //  Find a starting point.
  for (i=0; i<points; i++) if (y[i]>newY || y[i]==newY && x[i]<newX) {
    newX=x[i]; newY=y[i]; }
  *polyCorners=0;

  //  Polygon-construction loop.
  while (!(*polyCorners) || newX!=polyX[0] || newY!=polyY[0]) {
    polyX[*polyCorners]=newX;
    polyY[*polyCorners]=newY; minAngleDif=CIRCLE_RADIANS;
    for (i=0; i<points; i++) {
      xDif=x[i]-polyX[*polyCorners];
      yDif=y[i]-polyY[*polyCorners];
      if (xDif || yDif) {
        newAngle=angleOf(xDif,yDif);     angleDif =oldAngle-newAngle;
        while (angleDif< 0.            ) angleDif+=CIRCLE_RADIANS;
        while (angleDif>=CIRCLE_RADIANS) angleDif-=CIRCLE_RADIANS;
        if (angleDif<minAngleDif) {
          minAngleDif=angleDif; newX=x[i]; newY=y[i]; }}}
    (*polyCorners)++; oldAngle+=.5*CIRCLE_RADIANS-minAngleDif; }}