哈夫曼压缩与解压缩学习笔记(一)
前言
看了两个哈夫曼压缩程序,学习了一把,选一个压缩和解压缩效率高的作些笔记.
一、哈夫曼压缩原理
我们知道计算机中的文件采用二进制编码,为了使文件尽可能的缩短(压缩),可以对文件中每个字节出现的次数进行统计,设法让出现次数多的字节的二进制码短些,而让那些很少出现的字节的二进制码长一些,这便使整个文件编码之后的总长度的平均期望长度降低,从而达到无损压缩数据的目的。哈夫曼uffman于1952年提出一种编码方法(算法),该方法完全依据字符(字节)出现概率来生成字符的二进制编码,而且可以证明 Huffman 算法在无损压缩算法中是最优的, 一般就叫作Huffman编码。Huffman 原理简单,实现起来也不困难,得到了广泛的应用。对应用程序、重要资料等绝对不允许信息丢失的压缩场合, Huffman 压缩是非常好的选择。
二、哈夫曼树及哈夫曼编码生成步骤:
① 扫描要压缩的文件,对字节出现的频率进行计算统计。
② 把字节按出现的频率进行排序,组成一个队列。
③ 把出现频率(权值)最低的两个字节作为叶子节点,它们的权值之和为根节点组成一棵树。
④ 把上面叶子节点的两个字节从队列中移除,并把它们组成的根节点加入到队列。
⑤ 把队列重新进行排序。重复步骤 ③④⑤ 直到队列中只有一个节点为止。
⑥ 把这棵树上的根节点定义为 0 (可自行定义 0 或 1 )左边为 0 ,右边为 1 。这样就可以得到每个叶子节点的哈夫曼编码了。
例:假设有一段文件"ASCTASCTAAAAACCTTT",其中用到4个不同字符A,C,S,T,它们在文件中出现的次数分别为 7 , 2 , 4 , 5 。把 7 , 2 , 4 , 5 当做 4 个叶子的权值用上述方法构造的哈夫曼树如图所示。
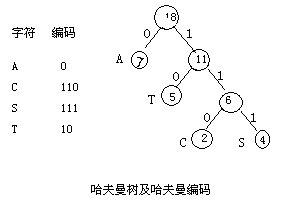
在树中令所有左分支取编码为 0 ,令所有右分支取编码为1。将从根结点起到某个叶子结点路径上的各左、右分支的编码顺序排列,就得这个叶子结点所代表的字符的二进制编码(哈夫曼编码),如上图所示。
这些编码拼成的文件"01111101001111101000000110110101010"不会混淆,因为每个字符的编码均不是其他编码的前缀,这种编码称做前缀编码。
三、压缩和解压缩文件
哈夫曼编码生成以后,所谓的压缩文件不过是将文件中每一个字节读出后用其哈夫曼编码替换,满八位后写入压缩文件,不满八位的读出下一字节凑成八位,这样边读边写,直到文件末尾.
解压缩过程与压缩过程相反,从压缩文件中读一字节(八位)缓存,然后一位一位的解码,直到读到一个哈夫曼编码,用其对应的字节数据替换写入解压文件,这样边读边解码边写,直到文件末尾.
当然写压缩文件内容前,要先写入码表(原文件的编码信息:字节----频率)用于解压缩时还原哈夫曼树及哈夫曼编码。
四、代码学习
末完待续......
看了两个哈夫曼压缩程序,学习了一把,选一个压缩和解压缩效率高的作些笔记.
一、哈夫曼压缩原理
我们知道计算机中的文件采用二进制编码,为了使文件尽可能的缩短(压缩),可以对文件中每个字节出现的次数进行统计,设法让出现次数多的字节的二进制码短些,而让那些很少出现的字节的二进制码长一些,这便使整个文件编码之后的总长度的平均期望长度降低,从而达到无损压缩数据的目的。哈夫曼uffman于1952年提出一种编码方法(算法),该方法完全依据字符(字节)出现概率来生成字符的二进制编码,而且可以证明 Huffman 算法在无损压缩算法中是最优的, 一般就叫作Huffman编码。Huffman 原理简单,实现起来也不困难,得到了广泛的应用。对应用程序、重要资料等绝对不允许信息丢失的压缩场合, Huffman 压缩是非常好的选择。
二、哈夫曼树及哈夫曼编码生成步骤:
① 扫描要压缩的文件,对字节出现的频率进行计算统计。
② 把字节按出现的频率进行排序,组成一个队列。
③ 把出现频率(权值)最低的两个字节作为叶子节点,它们的权值之和为根节点组成一棵树。
④ 把上面叶子节点的两个字节从队列中移除,并把它们组成的根节点加入到队列。
⑤ 把队列重新进行排序。重复步骤 ③④⑤ 直到队列中只有一个节点为止。
⑥ 把这棵树上的根节点定义为 0 (可自行定义 0 或 1 )左边为 0 ,右边为 1 。这样就可以得到每个叶子节点的哈夫曼编码了。
例:假设有一段文件"ASCTASCTAAAAACCTTT",其中用到4个不同字符A,C,S,T,它们在文件中出现的次数分别为 7 , 2 , 4 , 5 。把 7 , 2 , 4 , 5 当做 4 个叶子的权值用上述方法构造的哈夫曼树如图所示。

在树中令所有左分支取编码为 0 ,令所有右分支取编码为1。将从根结点起到某个叶子结点路径上的各左、右分支的编码顺序排列,就得这个叶子结点所代表的字符的二进制编码(哈夫曼编码),如上图所示。
这些编码拼成的文件"01111101001111101000000110110101010"不会混淆,因为每个字符的编码均不是其他编码的前缀,这种编码称做前缀编码。
三、压缩和解压缩文件
哈夫曼编码生成以后,所谓的压缩文件不过是将文件中每一个字节读出后用其哈夫曼编码替换,满八位后写入压缩文件,不满八位的读出下一字节凑成八位,这样边读边写,直到文件末尾.
解压缩过程与压缩过程相反,从压缩文件中读一字节(八位)缓存,然后一位一位的解码,直到读到一个哈夫曼编码,用其对应的字节数据替换写入解压文件,这样边读边解码边写,直到文件末尾.
当然写压缩文件内容前,要先写入码表(原文件的编码信息:字节----频率)用于解压缩时还原哈夫曼树及哈夫曼编码。
四、代码学习
(1)BitUtils.java 定义用到的常量
public interface BitUtils {
public static final int BITS_PER_BYTES = 8;
public static final int DIFF_BYTES = 256;
public static final int EOF = 256;
}
(2)CharCounter.java
这个类用于字节计数。其带参构造函数打开一个流文件,从流中读取每一个字节,统计每个字节出现的次数(频数),存于数组tehCounts中,其charCountSum()方法统计流文件中总的字节数
import java.io.*;
public class CharCounter {//字节计数器
private int [ ] theCounts = new int[ BitUtils.DIFF_BYTES + 1 ];
public CharCounter( )
{
}
public CharCounter( InputStream input ) throws IOException
{
int ch;
//从流中读一个字节,返回0到255范围内的int字节值
while( ( ch = input.read( ) ) != -1 )
theCounts[ ch ]++;//计数
}
public int getCount( int ch )//获取字节ch的频数
{
return theCounts[ ch & 0xff ];
}
public void setCount( int ch, int count )//设置字节ch的频数
{
theCounts[ ch & 0xff ] = count;
}
public long charCountSum()//统计流中所有字节数
{
long sum=0;
int count=theCounts.length;
int i=0;
while(i<count)
{
sum=sum+theCounts[i];
i++;
}
return sum;
}
}
末完待续......