本文假设读者至少有对数据挖掘中的关联规则有基本了解,对Apriori算法的实现有一定了解。
在此基础上,我们讨论一种比Apriori更加高效的关联规则挖掘方法——基于FP-Tree的关联规则挖掘。
(一) 关于Apriori:
Apriori是关联规则挖掘中最最最经典的算法,没有之一。同时,它也是向初学同学阐明关联规则精髓的最佳武器。
首先,我们简单回顾下Apriori算法的两个概念:
频繁项集:即支持度不小于指定的最小支持度的项集就是频繁项集。
向下封闭:如果k项候选集中有一项不是频繁项集,则这个k项集也不是频繁项集。
它的主要问题是:
在由频繁k项集生成频繁k+1项集时,需要将每个组合得到的候选k+1项集在事务数据中扫描一遍。以此来判断生成的k+1项集是否是频繁项集。
这就意味着,整个计算过程中,它会多次地重复扫描事务数据,导致了其效率比较低下。
(二) 基于FP-Tree计算频繁2项集
这里之所以只计算频繁2项集,是因为:
1. 我们应用中,绝大多数情况下,只需要挖掘到2项集,即满足最小支持度的pair 对,如:<left_item,right_item>
2. 你会发现,如果你掌握了如何用FP-Tree生成频繁2项集,那生成频繁N项集就只是多走那么一小步了哈。
这里我们先简单介绍下基于FP-Tree的关联规则算法:
更官方的名字应该是FP-growth算法(Frequent Pattern-growth),它使用一种紧缩的数据结构来存储查找频繁项集所需要的全部信息。这里的FP-Tree就是FP-growth算法中用到的这种紧缩数据结构。
更多的关于FP-Tree和FP-growth算法的信息可参考百度百科或者直接在百度搜索。。。
接下来,我们使用Bash Shell来编码实现基于FP-Tree的频繁二项集挖掘。
假设,我们有如下事务数据文件:
A,B,E,C
A,B,C
A,D
A,B
A,E
并且假设,我们指定最小支持度为2.
则我们可目测得到结果如下:
B,A:3
C,A:2
C,B:2
E,A:2
接下来,我们通过如下代码来得到我们想要的结果:
#!/home/admin/bin/bash_bin/bash_4
if [ $# -ne 2 ]; then
echo "please input the trans input file";
exit 1;
fi
trans_file=$1;
min_support=$2;
if [ "x$trans_file" == "x" ]; then
echo "the input file can not be null";
exit 2;
fi
if [ ! -f "$trans_file" ]; then
echo "trans should be a existed data file"
exit 3;
fi
if [ -z "$min_support" ]; then
echo "please specify the min support for the freq-2 items"
exit 4;
fi
## get the freq-1 items and the frequents for each of them
declare -A freq_1;
for line in `cat $trans_file`
do
currentItemArray=(${line//,/ });
for i in ${currentItemArray[@]}
do
if [ -z ${freq_1[$i]} ]; then
freq_1[$i]=1;
else
((freq_1[$i]+=1));
fi
done
done
for k in ${!freq_1[@]}
do
if [ ${freq_1[$k]} -lt $min_support ]; then
unset freq_1[$k];
fi
done
### sort the freq_1 using external sort commond
declare -a freq_1_sorted_item;
freq_1_sorted_length=0;
for i in `
for i in ${!freq_1[@]}
do
echo "$i,${freq_1[$i]}"
done | sort -s -t ',' -k 2 -nr
`
do
freq_1_sorted_item[$freq_1_sorted_length]=${i%%,*};
((freq_1_sorted_length+=1));
done
### Generate the FP-Tree using a one dimensional array with a virtual root node
### The element with struct {itemName:Support:Child:Next:Parent}
### The virtual root node is {NULL:0:0:0:0} that the only Child filed will not be '0'.
### Because it has no parent and no sibling nodes and no support.
declare -a FP_TREE; ## this is the fp_tree
declare -A Node_Index; ## the index of each freq_1 item
### push the virtual root node
FP_TREE[0]="NULL:0:0:0:0";
### scan the trans file again and also the last time.
### and generate the fp_tree
for line in `cat $trans_file`
do
### scan the sorted freq_1 items
### no need to sort the original trans input line....
current_node_index=0;
for freq_1_item in ${freq_1_sorted_item[@]}
do
if [[ ",$line," == *",$freq_1_item,"* ]]; then
current_node_line=${FP_TREE[$current_node_index]};
current_node_info=(${current_node_line//:/ });
child_index=${current_node_info[2]};
if [ "$child_index" == "0" ]; then
### add a new node as the first left child of the current node
new_node="$freq_1_item:1:0:0:$current_node_index";
FP_TREE_LENGTH=${#FP_TREE[@]};
FP_TREE[$FP_TREE_LENGTH]=$new_node;
### update the child pointer of the current node
current_node_info[2]=$FP_TREE_LENGTH;
tmp_line=${current_node_info[*]};
FP_TREE[$current_node_index]=${tmp_line// /:};
current_node_index=$FP_TREE_LENGTH;
Node_Index[$freq_1_item]="${Node_Index[$freq_1_item]}:$current_node_index";
else
while :
do
child_node_line=${FP_TREE[$child_index]};
child_node_info=(${child_node_line//:/ });
### find a existed node match the current freq_1_item
if [ "${child_node_info[0]}" == "$freq_1_item" ]; then
((child_node_info[1]+=1));
tmp_line=${child_node_info[*]};
FP_TREE[$child_index]=${tmp_line// /:};
current_node_index=$child_index;
break;
fi
next_index=${child_node_info[3]};
if [ "$next_index" == "0" ]; then
### add a new node as the last child of the current node
### and also means the next node of the current last child node of the current node
new_node="$freq_1_item:1:0:0:$current_node_index";
FP_TREE_LENGTH=${#FP_TREE[@]};
FP_TREE[$FP_TREE_LENGTH]=$new_node;
### update the next pointer of the current last child of the current node
child_node_info[3]=$FP_TREE_LENGTH;
tmp_line=${child_node_info[*]};
FP_TREE[$child_index]=${tmp_line// /:};
current_node_index=$FP_TREE_LENGTH;
Node_Index[$freq_1_item]="${Node_Index[$freq_1_item]}:$current_node_index";
break;
fi
child_index=$next_index;
done
fi
fi
done
done ### FP_TREE Done!!!!!
fp_tree_length=${#FP_TREE[@]};
for((i=0;i<fp_tree_length;i++))
do
echo "$i->${FP_TREE[$i]}";
done
echo
### get the freq_2 items and their support from the FP_TREE!!!
declare -A item_4_freq2;
for freq_1_item in ${freq_1_sorted_item[@]}
do
treeIndex_item=${Node_Index[$freq_1_item]};
indexs=(${treeIndex_item//:/ });
base_support=0;
for index in ${indexs[@]}
do
p_node_line=${FP_TREE[$index]};
p_node_info=(${p_node_line//:/ });
current_path_support=${p_node_info[1]};
((base_support+=$current_path_support));
index=${p_node_info[4]};
## search the parent node until the root
while [ "$index" != "0" ]
do
p_node_line=${FP_TREE[$index]};
p_node_info=(${p_node_line//:/ });
p_item=${p_node_info[0]};
if [ -n "${item_4_freq2[$p_item]}" ]; then
((item_4_freq2[$p_item]+=$current_path_support));
else
item_4_freq2[$p_item]=$current_path_support;
fi
index=${p_node_info[4]};
done
done
for key in ${!item_4_freq2[@]}
do
freq_2_items_support=0;
[ $base_support -lt ${item_4_freq2[$key]} ] && ((freq_2_items_support=$base_support)) || ((freq_2_items_support=${item_4_freq2[$key]}));
if [ $freq_2_items_support -ge $min_support ]; then
echo "$freq_1_item,$key:$freq_2_items_support";
fi
unset item_4_freq2[$key];
done
done
关于代码的说明:
1. 代码中使用了关联数组,即你看到的declare -A *** 的部分,因此需要Bash4.0以上支持才能运行该代码。
2. 代码中首先扫描一次数据,生成了频繁1项集,并根据support对它们进行desc排序。
3. 根据生成的频繁1项集,第二次,也是最后一次扫描事务数据,生成FP-Tree,具体参见注释。
4. 最后根据生成的FP-Tree挖掘得到所有的频繁二项集,以及其支持度。
生成的FP-Tree:
如果你的机器上碰巧装有Bash4.0或以上版本时,可以运行该代码,可以看到生成的FP-Tree。
由于Bash不支持复合数据结构和多维数组,我只好通过结构化字符串的方式通过一维数组模拟FP-Tree。
代码中的FP-Tree:
FP-Tree节点的内部结构为{itemName:Support:Child:Next:Parent}
0->NULL:0:1:0:0
1->A:5:2:0:0
2->B:3:3:5:1
3->C:2:4:0:2
4->E:1:0:0:3
5->E:1:0:0:1
左边为node在数组中的位置。
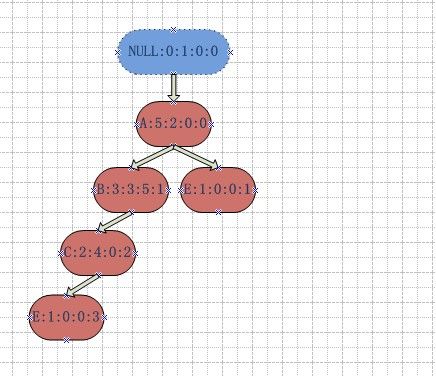
更直观的FP-Tree:
通过上述的输出信息,不难看出真实的树结构应该是这样的:
接下来就是根据这棵树,获取到我们需要的频繁二项集。
可能有人会说,这一步比原生的FP-growth算法要少做很多事情。
确实,因为我们这里只需要生成频繁2项集,因此不需要原本这一步中用来生成所有频繁项集的那些步骤。。。。
生成的频繁2项集如下:
B,A:3
C,A:2
C,B:2
E,A:2
具体可见代码:line156~line193。
在此就不做赘述了。。。
此外,代码运行命令:
./fp-tree-apriori.sh trans_input.dat 2
呵呵,你懂得。