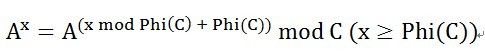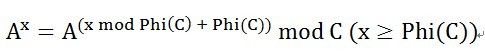- 如何用示波器的FFT计算功能抓取电机驱动DS两极间的辐射干扰源
Xyc0317_
硬件EMC单片机嵌入式硬件
1.硬件连接与准备探头选择:使用高带宽探头(至少为信号最高频率的3倍,例如1GHz探头用于300MHz干扰)。接地方式:采用探头接地弹簧而非长接地夹,缩短接地回路,减少引入噪声。差分测量(可选):若干扰为共模噪声,建议使用差分探头直接测量DS两极间电压。接线要点:尽量缩短探头与被测点的距离,避免环路天线效应。确保电机驱动电路处于正常工作状态(如PWM信号开启)。2.示波器参数设置(以泰克MSO5/
- 你的代码还在‘裸奔’?ASan & HWASN 内存漏洞修复实践(一)简介
月光技术杂谈
得力工具asanhwasan内存漏洞越界访问段错误稳定性可靠性
目录ASAN简介基本概念工作原理优势应用场景HWASanHWASan**与ASan的对比**本文首先简单介绍asan和hwasan的基本概念和区别,后续文章将详细介绍如何在arm平台或x86平台,利用asan/hwasan工具对大型协议软件进行内存问题分析。ASAN简介基本概念ASAN(AddressSanitizer)是一个由Google开发的、用于C和C++程序的快速内存错误检测工具,它能够在
- 正则表达式 匹配一次
zzyh123456
正则表达式mysql数据库
下面是一个概念性的示例,说明如何使用正则表达式来找到文本中的URL,并假设我们将基于这个URL的存在来构思一篇文章。正则表达式示例首先,定义正则表达式来匹配URL:regexhttps:\/\/www\.naquan\.com\/这个正则表达式会匹配字符串https://www.51969.com/。假设的Python脚本假设你有一个Python脚本,它使用正则表达式来查找文本中的URL,并基于这
- java nio编程实例_Java 网络IO编程总结(BIO、NIO、AIO均含完整实例代码)
weixin_39723010
javanio编程实例
1、BIO编程1.1、传统的BIO编程网络编程的基本模型是C/S模型,即两个进程间的通信。服务端提供IP和监听端口,客户端通过连接操作想服务端监听的地址发起连接请求,通过三次握手连接,如果连接成功建立,双方就可以通过套接字进行通信。传统的同步阻塞模型开发中,ServerSocket负责绑定IP地址,启动监听端口;Socket负责发起连接操作。连接成功后,双方通过输入和输出流进行同步阻塞式通信。简单
- 【Java进阶篇】——第11篇:Java 8 新特性及使用
猿享天开
Java开发从入门到精通java开发语言
第11篇:Java8新特性及使用Java8是一次里程碑式的更新,引入了多项革新特性,极大地提升了开发效率和代码表现力。本文将从Lambda表达式、StreamAPI、时间日期API、Optional类等核心特性出发,结合实战场景和最佳实践,全面解析Java8的核心功能。1.Lambda表达式与函数式编程1.1Lambda表达式基础Lambda表达式允许以简洁的语法实现函数式接口(仅含一个抽象方法的
- LineageOS的代码下载、编译及真机运行
ironlzz
个人笔记LineageOSAndroid
最近给电脑换了块硬盘,重装完系统重新下载代码时,发现很多细节都忘记了,尤其是环境搭建这种只做一次的工作,因此有必要把步骤记录一下,以便后续查阅。LineageOS是一个开源的Android系统,代码基本与AOSP相同,LineageOS支持更多的设备,门槛更低。官网地址:https://wiki.lineageos.org前期准备:LineageOS的代码环境要求与AOSP类似,首先安装curl以
- 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 【2023】
梦想橡皮擦
excel华为python算法华为od
最近更新的博客华为OD机试题-最短耗时(JavaScript)华为OD机试题-机器人走迷宫(JavaScript)华为OD机试-新员工座位安排系统(Python)|机试题算法思路华为OD机试-能力组队(Python)|机试题算法思路华为OD机试-内存池(Python)|机试题算法思路使用说明参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。华为OD清单查看地址:bl
- 【论文投稿-第五届人工智能与工业技术应用国际学术会议(AIITA 2025)】编程语言大比拼:C、C++、Python 和 Java
禁默
话题探讨学术会议c语言c++python
第五届人工智能与工业技术应用国际学术会议(AIITA2025)将于2025年3月28-30日在中国西安举行。会议旨在为从事人工智能、智能制造、自动化等领域的专家学者、工程技术人员、研发人员提供一个共享科研成果和前沿技术,了解学术发展趋势,拓宽研究思路,加强学术研究和探讨,促进学术成果产业化合作的平台。编辑AIITA2025已上线至IEEE官方列表,详情请点击....大会时间:2025年3月28日-
- 软件测试技术之跨平台的移动端UI自动化测试(上)
学掌门
软件测试ITui软件测试
摘要:本文提出一种跨平台的UI自动化测试方案,一方面使用像素级的截图对比技术,解决传统UI自动化测试难以验证页面样式的问题;另一方面用统一部署在服务器端的JavaScript测试代码代替Android和iOS测试代码,大大提高编写测试代码的效率。该方案经过实际验证,具有效率高、质量好、便于维护等多方面优点,文中将阐述具体设计思路以及各关键步骤的实现方法,为同类测试提供借鉴。一、背景当前金融服务数字
- python_excel批量插入图片
ramsey17
pythonexcel
提取excel的指定列的值的后4位(数值),在其它列名的单元格中,批量嵌入与该数值匹配的图片(未实现居中),每间隔4行处理一次(合并过单元格)。importpandasaspdfromopenpyxlimportload_workbookfromopenpyxl.drawing.imageimportImagefromopenpyxl.utilsimportget_column_letterimp
- 大模型进化论:AI产业落地将卷向何方?
科技云报道
人工智能大数据
科技云报到原创。2024年,是大模型翻天覆地的一年。“百模大战”爆发不久,大模型价格战随之而来,成本高昂的大模型几乎进入了免费时代。大模型从庞大的实验室工具,转变为高效灵活的应用助手,以狂飙猛进的速度在众多行业落地生根。不再有人质疑大模型是“拿着锤子找钉子”,更急迫的需求来自市场端。行业对大模型应用的渴望推动着AIAgent走向前台,围绕AIAgent的混战已然开启。与此同时,大模型的技术范式飞速
- 科技云报到:从大模型到云端,“AI+云计算”还能讲出什么新故事
科技云报道
云计算大模型云计算
科技云报到原创。2024年的大模型产业,注定将是会被反复提起的一页。这一年,被按下加速键的市场刚刚过半,就已经显示出冰火两重天的格局。算法的单模态扩展到多模态,趋势如燎原之火,让全球陷入对世界模型畅想的狂欢中;一级市场逐渐走向冷静,投资人开始频频向企业要收入,百模齐发迅速被简化为几家独角兽之间的资本与技术持久战。云服务巨头则以一种标准制定者,以及顶级大模型团队背后力量的角色出现,成为市场中隐形的力
- 推动AI云产业向深向实,云·AI·算力创新发展大会即将启幕
科技云报道
云计算AI云计算
近年来,以AIGC为代表的新兴技术正加速演进,全球站在智能化变革的起点,人工智能与云计算的深度融合,也驱动云计算进入第三次发展浪潮,迎来前所未有的机遇。伴随AI的快速发展,2024年《政府工作报告》明确提出,制定支持数字经济高质量发展政策,深化大数据、人工智能等研发应用,开展“人工智能+”行动。这意味着AI正在成为产业创新的核心抓手和驱动新质生产力的关键引擎,而云计算作为基础底座将在其中扮演至关重
- 6. 火尖枪破回文 - 最长回文子串(中心扩散法)
轻口味
java算法前端cppc++
哪吒在数据修仙界中继续他的修炼之旅。这一次,他来到了一片神秘的回文森林,森林中弥漫着神秘的气息。森林的入口处有一块巨大的石碑,上面刻着一行文字:“欲破此林,需以火尖枪之力,破回文之障,寻最长回文子串。”哪吒定睛一看,石碑上还有一行小字:“字符串"babad"中,最长回文子串为"bab"或"aba"。”哪吒心中一动,他知道这是一道关于寻找最长回文子串的难题,需要找到一个字符串中最长的正读和反读都相同
- mac m1通过qemu和grub制作操作系统引导盘
千篇不一律
深入学习操作系统macos数据库
文章目录前言grub安装引导盘FAQ参考附录qemu安装ubuntuGRUB安装到回环设备吧啦吧啦...前言我电脑是macm1芯片的,做了如下尝试,最终在第4种方式下成功:开始用了parallelsdesktop安装了ubuntu22版本的,因为本机是arm64芯片,所以只能安装arm64的ubuntu,然后在运行grub-install/dev/loop0时报错:grub-install:err
- BabyAGI:开创智能自动化新时代,赋能人工智能的下一次飞跃
gs80140
基础知识科谱AI人工智能自动化运维
目录BabyAGI:开创智能自动化新时代,赋能人工智能的下一次飞跃什么是BabyAGI?BabyAGI的核心功能BabyAGI的应用领域BabyAGI与传统AI系统的区别BabyAGI的挑战与未来发展BabyAGI的未来展望结语BabyAGI:开创智能自动化新时代,赋能人工智能的下一次飞跃随着人工智能(AI)的不断演进,机器学习和自我优化系统已经逐步渗透到各个行业,从医疗健康到金融服务,从零售到制
- 写好C/C++代码,大学生必读:林锐博士的《高质量 C++/C 编程指南》
晚风る
C\C++c++c语言
作为一名大学生,我深知在学习编程的过程中,写出高质量的代码是多么重要。最近,我读了林锐博士的《高质量C++/C编程指南》,这本书让我受益匪浅,今天想和大家分享一下我的学习心得。目录一、初识《高质量C++/C编程指南》二、书中的精华内容(一)编程规范与代码风格(二)内存管理(三)函数设计(四)类的构造函数、析构函数与赋值函数三、我的学习与实践四、收获与感悟五、推荐与分享一、初识《高质量C++/C编程
- 版本控制与Git实战指南:从入门到WebStorm集成
The god of big data
教程大Big数据Data建站gitwebstormelasticsearch
一、版本控制:数字时代的时光机器在软件开发的世界里,每一次代码修改都如同一次时间旅行。版本控制系统(VersionControlSystem)正是这个领域的时光机器,它不仅能完整记录项目的演化历史,更能让开发者自由穿梭于各个版本之间。Git作为分布式版本控制系统的代表,已成为全球开发者必备的核心工具。Git与传统版本控制系统(如SVN)的关键差异:分布式架构:每个开发者都拥有完整的仓库副本闪电级操
- 用realsense d435i传感器在实际环境中跑ORB_SLAM3,顺带解决一部分编译问题
睫力上爬
SLAM日常折腾传感器ORB_SLAM3
是的ORB_SLAM3来了,时隔五年,它来带的惊喜到底是啥呢?一个完全依赖于最大后验估计(MAP)的单/双目惯导融合系统高回召的地点识别功能(High-recallplacerecognition)第一个完整的多地图系统(multi-map)一个抽象的相机模型表示论文地址论文细节今天不说,今天主要先拿到代码,并且用自己的传感器试试实际效果编译终端拉代码记得提前安装好OpenCV,Eigen,和Pa
- python aiohttp_Python-异步之aiohttp
weixin_39864101
pythonaiohttp
什么是aiohttp?一个异步的HTTP客户端\服务端框架,基于asyncio的异步模块。可用于实现异步爬虫,更快于requests的同步爬虫。aiohttp和requestsrequests版爬虫requests同步方式连续30次简单爬取http://httpbin.org网站importrequestsfromdatetimeimportdatetimedeffetch(url):r=requ
- C++ -- vector的模拟实现
kk\n
c++开发语言
vector.h的内容:#pragmaonce#include#include#includenamespacekk{templateclassvector{public:typedefT*iterator;//指针版迭代器typedefconstT*const_iterator;//注:这里的bgein()、end()写的都是用的传值返回,所以不能对返回值进行++,--这种操作(就是++v.be
- C++中的内存管理
kk\n
c++开发语言
文章目录1.C/C++内存分布2.C语言中动态内存管理方式3.C++中动态内存管理4.operatornew与operatordelete函数5.new和delete的实现原理6.定位new表达式(placement-new)7.一些常见的问题和有关内存泄漏的知识1、C/C++内存分布我们先来看下面的一段代码和相关问题#includeintglobalVar=1;staticintstaticGl
- Golang学习笔记_31——原型模式
LuckyLay
Golang学习笔记golang学习笔记原型模式
Golang学习笔记_28——工厂方法模式Golang学习笔记_29——抽象工厂模式Golang学习笔记_30——建造者模式文章目录一、原型模式核心概念1.定义2.解决的问题3.核心角色4.类图二、原型模式的特点三、适用场景1.对象创建成本高2.需要动态配置对象3.避免重复初始化4.需要隔离对象构造细节四、与其他创建型模式的对比五、Go语言代码示例六、原型模式的高级用法1.原型注册表2.动态配置对
- C++ primer plus
C_VuI
c++
C++primerplus(第六版)文章目录C++primerplus(第六版)梗概梗概编程世界日新月异,各种编程语言层出不穷,但C++始终凭借其高效、灵活和强大的性能在众多领域占据着重要地位。当我们决定踏入C++的学习领域时,一本好的教材就显得尤为关键。《C++PrimerPlus》正是这样一本兼具权威性和实用性的经典书籍,它陪伴了一代又一代的程序员成长。作为一名对C++充满热情的学习者,我在阅
- es6中的generator函数详解
2401_89308368
es6前端ecmascript
但是,调用Generator函数后,函数并不执行,返回的也不是函数执行后的结果,而是一个指向内部状态的指针对象。下一步,必须调用遍历器对象的next方法,使得指针移向下一个状态。即:每次调用next方法,内部指针就从函数头部或上一次停下来的地方开始执行,直到遇到下一个yield表达式(或return语句)为止。Generator函数是分段执行的,yield表达式是暂停执行的标记,而next方法可以
- 奥比中光3D机器视觉相机能连接halcon吗?
视觉人机器视觉
机器视觉3D3d数码相机视觉检测c#
奥比中光的设备与Halcon的兼容性可以通过以下方式实现:数据接口的通用性奥比中光的相机(如AstroPro、大白等)支持通过UVC协议获取彩色图像,深度数据则通过OpenNI或ROS2接口传输105。若Halcon支持这些协议或标准接口(如ROS消息、OpenCV图像流),则可通过直接调用或二次开发实现连接。例如,通过Python或C#脚本将图像数据从相机传输至Halcon的处理流程中。SDK与
- C++ -- stack的模拟实现 && 介绍适配器模式
kk\n
c++开发语言适配器模式
适配器模式(一种设计模式)/配接器什么是适配器:例如充电器就叫做电源适配器本质:就是一种转换虽然stack和queue中也可以存放元素,但在STL中并没有将其划分在容器的行列,而是将其称为容器适配器,这是因为stack和queue都是对其他容器进行了封装,STL中stack和queue默认封装的是deque。template>//库里用的是一个叫做deque的容器来做缺省参数补充:deque(双端
- 咱们一起学C++ 第二百零三篇:之C++中protected关键字与私有继承的深入探究
一杯年华@编程空间
咱们一起学习C++java算法开发语言
咱们一起学C++第二百零三篇:之C++中protected关键字与私有继承的深入探究大家好!C++作为一门强大的编程语言,有着丰富多样的特性,今天咱们来深入学习protected关键字以及私有继承相关的知识。希望通过这次学习,我们能更好地掌握C++的类继承机制,在编程之路上共同进步!一、private继承的详细剖析在C++中,私有继承是一种特殊的继承方式。当一个类私有继承另一个类时,基类的所有成员
- C++混合字符串排序
Echo-Tian
算法竞赛c++正则表达式stl字符串
题一:有一个txt文件,里面都是空格或者回车分隔的英文单词。请写一个程序,输入文件名,输出文件中出现次数最多的前20个单词。1,使用unordermap统计字符出现次数2,将unordermap统计后的次数转化成pair的vector,3,调用sort函数自定义排序规则进行排序。#include#include#include#include#include#include#include#inc
- 【C++文件读写操作】IO流读文件[程序和文件必须在同一文件夹]
超级码力666
c++
郑书p505习题3:使用IO流以文本方式建立一个文件test1.txt(我存在了D盘的demo2文件夹下),注意程序和文件必须在同一文件夹下代码解释1.ofstreamfile(“test1.txt”);①创建一个ofstream对象file,用于写入文件②没有文件会自动创建文件;已有文件会覆盖原内容2.fileusingnamespacestd;intmain(){//创建一个ofstream对
- Java常用排序算法/程序员必须掌握的8大排序算法
cugfy
java
分类:
1)插入排序(直接插入排序、希尔排序)
2)交换排序(冒泡排序、快速排序)
3)选择排序(直接选择排序、堆排序)
4)归并排序
5)分配排序(基数排序)
所需辅助空间最多:归并排序
所需辅助空间最少:堆排序
平均速度最快:快速排序
不稳定:快速排序,希尔排序,堆排序。
先来看看8种排序之间的关系:
1.直接插入排序
(1
- 【Spark102】Spark存储模块BlockManager剖析
bit1129
manager
Spark围绕着BlockManager构建了存储模块,包括RDD,Shuffle,Broadcast的存储都使用了BlockManager。而BlockManager在实现上是一个针对每个应用的Master/Executor结构,即Driver上BlockManager充当了Master角色,而各个Slave上(具体到应用范围,就是Executor)的BlockManager充当了Slave角色
- linux 查看端口被占用情况详解
daizj
linux端口占用netstatlsof
经常在启动一个程序会碰到端口被占用,这里讲一下怎么查看端口是否被占用,及哪个程序占用,怎么Kill掉已占用端口的程序
1、lsof -i:port
port为端口号
[root@slave /data/spark-1.4.0-bin-cdh4]# lsof -i:8080
COMMAND PID USER FD TY
- Hosts文件使用
周凡杨
hostslocahost
一切都要从localhost说起,经常在tomcat容器起动后,访问页面时输入http://localhost:8088/index.jsp,大家都知道localhost代表本机地址,如果本机IP是10.10.134.21,那就相当于http://10.10.134.21:8088/index.jsp,有时候也会看到http: 127.0.0.1:
- java excel工具
g21121
Java excel
直接上代码,一看就懂,利用的是jxl:
import java.io.File;
import java.io.IOException;
import jxl.Cell;
import jxl.Sheet;
import jxl.Workbook;
import jxl.read.biff.BiffException;
import jxl.write.Label;
import
- web报表工具finereport常用函数的用法总结(数组函数)
老A不折腾
finereportweb报表函数总结
ADD2ARRAY
ADDARRAY(array,insertArray, start):在数组第start个位置插入insertArray中的所有元素,再返回该数组。
示例:
ADDARRAY([3,4, 1, 5, 7], [23, 43, 22], 3)返回[3, 4, 23, 43, 22, 1, 5, 7].
ADDARRAY([3,4, 1, 5, 7], "测试&q
- 游戏服务器网络带宽负载计算
墙头上一根草
服务器
家庭所安装的4M,8M宽带。其中M是指,Mbits/S
其中要提前说明的是:
8bits = 1Byte
即8位等于1字节。我们硬盘大小50G。意思是50*1024M字节,约为 50000多字节。但是网宽是以“位”为单位的,所以,8Mbits就是1M字节。是容积体积的单位。
8Mbits/s后面的S是秒。8Mbits/s意思是 每秒8M位,即每秒1M字节。
我是在计算我们网络流量时想到的
- 我的spring学习笔记2-IoC(反向控制 依赖注入)
aijuans
Spring 3 系列
IoC(反向控制 依赖注入)这是Spring提出来了,这也是Spring一大特色。这里我不用多说,我们看Spring教程就可以了解。当然我们不用Spring也可以用IoC,下面我将介绍不用Spring的IoC。
IoC不是框架,她是java的技术,如今大多数轻量级的容器都会用到IoC技术。这里我就用一个例子来说明:
如:程序中有 Mysql.calss 、Oracle.class 、SqlSe
- 高性能mysql 之 选择存储引擎(一)
annan211
mysqlInnoDBMySQL引擎存储引擎
1 没有特殊情况,应尽可能使用InnoDB存储引擎。 原因:InnoDB 和 MYIsAM 是mysql 最常用、使用最普遍的存储引擎。其中InnoDB是最重要、最广泛的存储引擎。她 被设计用来处理大量的短期事务。短期事务大部分情况下是正常提交的,很少有回滚的情况。InnoDB的性能和自动崩溃 恢复特性使得她在非事务型存储的需求中也非常流行,除非有非常
- UDP网络编程
百合不是茶
UDP编程局域网组播
UDP是基于无连接的,不可靠的传输 与TCP/IP相反
UDP实现私聊,发送方式客户端,接受方式服务器
package netUDP_sc;
import java.net.DatagramPacket;
import java.net.DatagramSocket;
import java.net.Ine
- JQuery对象的val()方法执行结果分析
bijian1013
JavaScriptjsjquery
JavaScript中,如果id对应的标签不存在(同理JAVA中,如果对象不存在),则调用它的方法会报错或抛异常。在实际开发中,发现JQuery在id对应的标签不存在时,调其val()方法不会报错,结果是undefined。
- http请求测试实例(采用json-lib解析)
bijian1013
jsonhttp
由于fastjson只支持JDK1.5版本,因些对于JDK1.4的项目,可以采用json-lib来解析JSON数据。如下是http请求的另外一种写法,仅供参考。
package com;
import java.util.HashMap;
import java.util.Map;
import
- 【RPC框架Hessian四】Hessian与Spring集成
bit1129
hessian
在【RPC框架Hessian二】Hessian 对象序列化和反序列化一文中介绍了基于Hessian的RPC服务的实现步骤,在那里使用Hessian提供的API完成基于Hessian的RPC服务开发和客户端调用,本文使用Spring对Hessian的集成来实现Hessian的RPC调用。
定义模型、接口和服务器端代码
|---Model
&nb
- 【Mahout三】基于Mahout CBayes算法的20newsgroup流程分析
bit1129
Mahout
1.Mahout环境搭建
1.下载Mahout
http://mirror.bit.edu.cn/apache/mahout/0.10.0/mahout-distribution-0.10.0.tar.gz
2.解压Mahout
3. 配置环境变量
vim /etc/profile
export HADOOP_HOME=/home
- nginx负载tomcat遇非80时的转发问题
ronin47
nginx负载后端容器是tomcat(其它容器如WAS,JBOSS暂没发现这个问题)非80端口,遇到跳转异常问题。解决的思路是:$host:port
详细如下:
该问题是最先发现的,由于之前对nginx不是特别的熟悉所以该问题是个入门级别的:
? 1 2 3 4 5
- java-17-在一个字符串中找到第一个只出现一次的字符
bylijinnan
java
public class FirstShowOnlyOnceElement {
/**Q17.在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b
* 1.int[] count:count[i]表示i对应字符出现的次数
* 2.将26个英文字母映射:a-z <--> 0-25
* 3.假设全部字母都是小写
*/
pu
- mongoDB 复制集
开窍的石头
mongodb
mongo的复制集就像mysql的主从数据库,当你往其中的主复制集(primary)写数据的时候,副复制集(secondary)会自动同步主复制集(Primary)的数据,当主复制集挂掉以后其中的一个副复制集会自动成为主复制集。提供服务器的可用性。和防止当机问题
mo
- [宇宙与天文]宇宙时代的经济学
comsci
经济
宇宙尺度的交通工具一般都体型巨大,造价高昂。。。。。
在宇宙中进行航行,近程采用反作用力类型的发动机,需要消耗少量矿石燃料,中远程航行要采用量子或者聚变反应堆发动机,进行超空间跳跃,要消耗大量高纯度水晶体能源
以目前地球上国家的经济发展水平来讲,
- Git忽略文件
Cwind
git
有很多文件不必使用git管理。例如Eclipse或其他IDE生成的项目文件,编译生成的各种目标或临时文件等。使用git status时,会在Untracked files里面看到这些文件列表,在一次需要添加的文件比较多时(使用git add . / git add -u),会把这些所有的未跟踪文件添加进索引。
==== ==== ==== 一些牢骚
- MySQL连接数据库的必须配置
dashuaifu
mysql连接数据库配置
MySQL连接数据库的必须配置
1.driverClass:com.mysql.jdbc.Driver
2.jdbcUrl:jdbc:mysql://localhost:3306/dbname
3.user:username
4.password:password
其中1是驱动名;2是url,这里的‘dbna
- 一生要养成的60个习惯
dcj3sjt126com
习惯
一生要养成的60个习惯
第1篇 让你更受大家欢迎的习惯
1 守时,不准时赴约,让别人等,会失去很多机会。
如何做到:
①该起床时就起床,
②养成任何事情都提前15分钟的习惯。
③带本可以随时阅读的书,如果早了就拿出来读读。
④有条理,生活没条理最容易耽误时间。
⑤提前计划:将重要和不重要的事情岔开。
⑥今天就准备好明天要穿的衣服。
⑦按时睡觉,这会让按时起床更容易。
2 注重
- [介绍]Yii 是什么
dcj3sjt126com
PHPyii2
Yii 是一个高性能,基于组件的 PHP 框架,用于快速开发现代 Web 应用程序。名字 Yii (读作 易)在中文里有“极致简单与不断演变”两重含义,也可看作 Yes It Is! 的缩写。
Yii 最适合做什么?
Yii 是一个通用的 Web 编程框架,即可以用于开发各种用 PHP 构建的 Web 应用。因为基于组件的框架结构和设计精巧的缓存支持,它特别适合开发大型应
- Linux SSH常用总结
eksliang
linux sshSSHD
转载请出自出处:http://eksliang.iteye.com/blog/2186931 一、连接到远程主机
格式:
ssh name@remoteserver
例如:
ssh ickes@192.168.27.211
二、连接到远程主机指定的端口
格式:
ssh name@remoteserver -p 22
例如:
ssh i
- 快速上传头像到服务端工具类FaceUtil
gundumw100
android
快速迭代用
import java.io.DataOutputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOExceptio
- jQuery入门之怎么使用
ini
JavaScripthtmljqueryWebcss
jQuery的强大我何问起(个人主页:hovertree.com)就不用多说了,那么怎么使用jQuery呢?
首先,下载jquery。下载地址:http://hovertree.com/hvtart/bjae/b8627323101a4994.htm,一个是压缩版本,一个是未压缩版本,如果在开发测试阶段,可以使用未压缩版本,实际应用一般使用压缩版本(min)。然后就在页面上引用。
- 带filter的hbase查询优化
kane_xie
查询优化hbaseRandomRowFilter
问题描述
hbase scan数据缓慢,server端出现LeaseException。hbase写入缓慢。
问题原因
直接原因是: hbase client端每次和regionserver交互的时候,都会在服务器端生成一个Lease,Lease的有效期由参数hbase.regionserver.lease.period确定。如果hbase scan需
- java设计模式-单例模式
men4661273
java单例枚举反射IOC
单例模式1,饿汉模式
//饿汉式单例类.在类初始化时,已经自行实例化
public class Singleton1 {
//私有的默认构造函数
private Singleton1() {}
//已经自行实例化
private static final Singleton1 singl
- mongodb 查询某一天所有信息的3种方法,根据日期查询
qiaolevip
每天进步一点点学习永无止境mongodb纵观千象
// mongodb的查询真让人难以琢磨,就查询单天信息,都需要花费一番功夫才行。
// 第一种方式:
coll.aggregate([
{$project:{sendDate: {$substr: ['$sendTime', 0, 10]}, sendTime: 1, content:1}},
{$match:{sendDate: '2015-
- 二维数组转换成JSON
tangqi609567707
java二维数组json
原文出处:http://blog.csdn.net/springsen/article/details/7833596
public class Demo {
public static void main(String[] args) { String[][] blogL
- erlang supervisor
wudixiaotie
erlang
定义supervisor时,如果是监控celuesimple_one_for_one则删除children的时候就用supervisor:terminate_child (SupModuleName, ChildPid),如果shutdown策略选择的是brutal_kill,那么supervisor会调用exit(ChildPid, kill),这样的话如果Child的behavior是gen_