Machine Learning系列实验--支持向量机SVM
理论部分见:http://www.cnblogs.com/biyeymyhjob/archive/2012/07/17/2591592.html
http://blog.csdn.net/sunmenggmail/article/details/7445035
//这个版本的代码仅可以算是初步实现,一些代码优化还有停止条件的选择还有待改进。
#include <iostream>
#include <cmath>
using namespace std;
#define N 12 //样本空间大小
#define C 4 //惩罚参数
#define M 2 //样本维数
double b = 4;//原始问题常数参数b
double W[M]; //原始问题参数
double A[N] = {0}; //初始化对偶问题参数
//训练样本
double X[N][M] = {
{1, 2},
{1, 1},
{-2, 2},
{2, 1},
{-2, 1},
{-1, 1},
{1, 4},
{2, 3},
{3, 2},
{-1, 4},
{-2, 3},
{-3, 2}
};
double Y[] = {-1, -1, -1,-1,-1,-1, 1, 1, 1, 1, 1, 1};
//kernel tricks
double Kernel (double *x, double *y, int length)
{
double sum = 0;
for (int k = 0; k < M; k++)
sum += pow(x[k] * y[k] ,2);//将x=(x1, x2)映射到z = (z1, z2) = (x1*x1, x2*x2)上,将x空间的椭圆变换成新空间里的直线,当然,这只是实验,核函数还有很多,具体选什么样的核函数还要视情况而定。
//return pow(sum, 2);
return sum;
}
//kernel tricks for samples
double K (int i, int j)
{
return Kernel(X[i], X[j], M);
}
//tool function
double Convert(double *x)
{
int j = 0;
double sum = 0;
for (j = 0; j < N; j++)
{
sum += A[j] * Y[j] * Kernel(X[j], x, M);
}
return sum;
}
//求Ei
double E(int i)
{
return Convert(X[i]) + b - Y[i];
}
//求函数间隔,与Ei仅差一个Yi
double g(double *x)
{
return Convert(x) + b;
}
//选择两个变量进行坐标下降
bool choose(int &a1, int &a2)
{
int i;
for (i = 0; i < N; ++i)
{
//选择违反KKT的a作为第一个的变量
if ((A[i] == 0 && Y[i] * g(X[i]) < 1) || (A[i] < C && A[i] > 0 && Y[i] * g(X[i]) != 1) || (A[i] == C && Y[i]*g(X[i]) > 1))
{
a1 = i;
break;
}
else if( i == N - 1)
{
return true; //当所有参数都满足KKT时停止,无法满足时?TODO:将可行间隙比率 增加为停止条件
}
}
double e1 = E(a1);
double e, e2, max = 0;
for (i = 0; i < N; i++)
{
if (i != a1)
{
e = E(i);
if (abs(e1-e) > max)
{
max = abs(e1 - e);
a2 = i;
e2 = e;
}
}
}
double L, H;
if (Y[a1] != Y[a2])
{
L = A[a2] - A[a1] > 0 ? A[a2] - A[a1] : 0;
H = C + A[a2] -A[a1] < C ? C + A[a2] -A[a1] :C;
}
else
{
L = A[a2] + A[a1] - C > 0 ? A[a2] + A[a1] - C : 0;
H = A[a2] + A[a1] < C ? A[a2] + A[a1] :C;
}
double temp = A[a2] + Y[a2] * (e1 - e2) / (K(a1, a1) + K(a2, a2) -2 * K (a1, a2));
double old = A[a2];
A[a2] = temp < L ? L : (temp > H ? H : temp); //更新a2
A[a1] = A[a1] + Y[a1]* Y[a2] * (old - A[a2]);//更新a1
return false;
}
double compute_b(int num, int a1, int a2)
{
double sum = 0;
int t = num == 1 ? a1: a2;
for (int i = 0; i < N; i++)
{
if (i != a1 && i!= a2)
sum += A[i] * Y[i] * K(i, t);
}
return Y[t] - sum - A[a1] * Y[a1] * K(a1, t) - A[a2] * Y[a2] * K(a2, t);
}
//SMO 算法解最优化对偶问题
void SMO()
{
int a1, a2;
double b1, b2;
int i =0;
while(true)
{
i++;
if (i > 100)
break;//当停止条件改进后,就不再需要
if (choose(a1, a2))
{
//满足KKT就停止
return;
}
else//更新b
{
b1 = compute_b(1, a1, a2);
b2 = compute_b(2, a1, a2);
if ((A[a1] < C && A[a1] > 0) && (A[a2] < C && A[a2]) > 0)
{
b = b1 ;
}
if ((A[a1] == 0 || A[a1] == C) && (A[a2] == 0 || A[a2] == C) )
{
b = (b1 + b2) / 2;
}
}
}
}
int main()
{
SMO();
double test[] = {0, -5};
cout << g(test) << endl;
return 0;
}
实验结果为:2.94999 ,说明(0,-5)点是正的,其他结果同样可以验证。
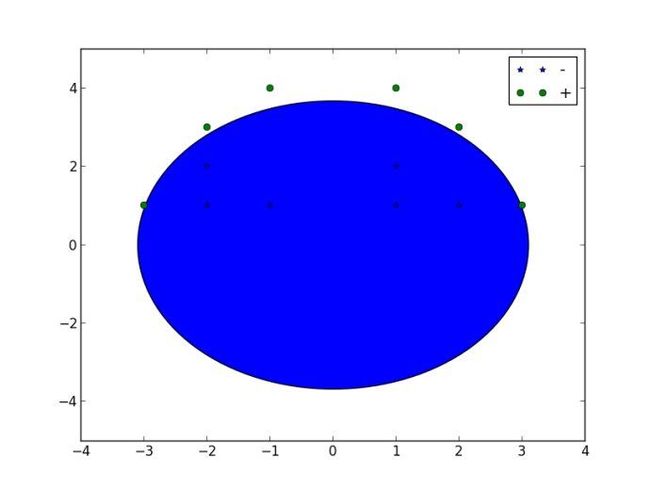
SVM分类结果图: