求解大规模有向图的所有连通分量
一 超大规模的稀疏图中的连通分量求解
背景
某地图厂商,需要检查道路网是否是连通的,比如是否存在孤岛(不能到达,也不能外出)?通常情况下,如果存在孤岛,说明道路勘测有问题。因此,随之而来的问题是:
(1)不考虑道路方向,是否所有道路都是连通的?
(2)如果考虑道路方向,是否任意2条道路均可以相互可达,如果不可以,输出可达情况,如存在path(u,v),但是不存在path(v,u)。
由于地图道路数据十分庞大,因此需要一个快速的算法/策略来实现目标,附加要求,内存不超过4G,时间4个小时,道路网,大约40M个点和40M条边。
这里先不假定这个附加要求的合理性,比如40m个点或者边可能是分布式存储。
无向图
表述:无向图G(E,V)中寻找各连通分量
1. 基本算法策略
因为是无向图,因此,BFS(广度优先搜索)或者DFS(深度优先搜索)都可以用来求各连通分量,其算法复杂度均为O(V+E)。但是,通常,大规模图都是稀疏图,DFS会占用大量的存储空间,因此使用BFS更加有效。
A. BFS算法
这个基本上数据结构或算法基础类的书籍都有,因此不阐述。注意,虽然DFS也是可以的,但是,遍历过程中会产生一很深的栈,无论是时间还是空间效率考虑,这算法是不合适的。
B. 等价关系算法
等价类的划分,需要使用一种叫做disjoint set的数据结构。一条边E(u,v)相当于u和v存在等价关系,即满足自反(self-clousure)、对称sysmetry,传递(transitivity)。因此,可以使用disjoint set结构来实现。算法复杂度O(ma(n))。 Ackerman是一个增长极为缓慢的函数,因此也可以认定复杂度也是O(V+E)。
C. 性能比较
BFS略优于Disjoint-set等价关系算法
最终,采用的是等价关系算法。理由:等价关系算法是个online算法,可以任意增加一条边,而不需要重新构造图G;不需要遍历vertex;适合分布式处理。
有向图
有向图的计算,实现难度要比无向图高很多。主要存在空间限制。为此,采用Divide & conquer思想来设计。很类似于分布式中的Map Reduce概念。
基本原理类同Map & Reduce,但是需要注意的:
A. 单机多线程并不能提高运行速度。实际上处理速度很快,主要瓶颈在存储空间限制。因此提高IO性能能够显著提高计算效率。
B. 主要限制在内存。因此需要使用外存来辅助进行归并。
1. 算法步骤
步骤:分为3个阶段:划分子图、计算子图、归并子图
(1) 划分子图(Partition Phase)
将数据分成各个partition,每个partition是一个独立的子图。
这里需要一个先验性的假设,划分子图能够较好的内聚性,即相邻的vertex划分后大多聚集在一个table中。
不能像普通的map-reduce的按照随机原则来划分。
在道路网状中,最好的方式是通过经纬度坐标来实现聚类划分。具体实现方式可以采用网格索引(速度最快,简单明了,但可能不够均匀和平衡)。
实际上,地图厂商都是按照省,或者城市来处理的,比如均匀网格划分的。因此,每个省作为一个子图是很合适,一个省的地图数据量完全可以在4G内存中完成。
图的划分用2种方式:Split Vertex 和Split Edges。
这里划分是边划分即Split Edges,即不切割顶点,只切割与顶点相关的边。
需要将所有切割的边保存,在后面的归并阶段需要使用。
(2) 计算子图(Do Phase)
<1> 求连通分量,执行SCC算法。——Robert Tarjan的强连通分量算法
计算完子图的连通性后,需要保存各子图以及该子图连通关系。
由于内存限制,每个子图通常需要保存为文件file(i)。用subgraph(i)表示相应第i个子图, scc(i,j),表示第i个子图,第j个强连通分量。
<2> 构建新坍缩子图
第i个子图对应的新的坍缩子图记为collapse_subgraph(i)。通常该子图也保存为文件。
A. 顶点集合。对改图的第j个连通分量Scc(j),使用该连通分量某个顶点(通常是Tranjan算法中,深度优先搜索生成树的根Root),记为root(u),作为新子图collpase_subgraph(i)的顶点集合。即原始顶点u所在连通分量都使用同一个顶点root(u)代替。
B. 边集合。添加各连通分量之间的边(从原始子图subgraph(i)中获得)到新collpase_subgraph(i)中,不需要添加重复边,如连通分量A,可以通过顶点a1,a2到达连通分量B,但从A到B仅需要添加一条边。
C. Collapse_subgraph实际上是个DAG图。当然可能存在独立的相互间都不可达的子图。这种容易出现在划分边界处。
(3) 归并子图 (Reduce)
归约过程也是一个合并图,并求其scc的过程。
以归约2个子图subgraph(i)和subgraph(j)为例:
找到步骤(2)子图i、j,subgraph(i),subgraph(j)对应的坍缩子图collapse(i),collapse(j)。
创建一个新的归并图merge_graph,将collapse(i),collapse(j)作为mergegraph的子图。(即添加其所有顶点和边到新的merge_graph中)。
<1> 对所有在步骤(1)中划分的边E(u,v),该边u、v满足分别属于两个子图i,j。
root(u), root(v),添加边E’(root(u),root(v)到新的merge_graph。同样,不需要添加重复边。
此时生成的是一个新的归并mergegraph。
通常是2个逻辑上相邻的子图进行归并,两两归并。因此,假设当前有N个子图,本趟归并需要[N/2 ]次。
(4) 循环
对步骤3生成的每个归并图merge_graph,重复步骤(2)、步骤(3),直到所有临时结果都已经归并。
2. 注意事项
在步骤2,3中,
第i个子图subggraph(i)中所有关联的顶点可以通过文件file(i)得到,但要查询某个顶点所在的子图(步骤2),需要使用hash表或者数据库。由于内存限制,最好使用数据库,如果使用文件,也需要单独对其建立索引,否则该步查找效率低,特别是频繁查找两个子图连接的分割边e(u,v),u,v属于两个不同的子图。另外,每次归并都需要保存临时结果。
由于I/O是程序瓶颈,需要建立合适的索引来检索顶点、边是,以减少整个程序的运行时间。
3. 算法分析
算法非常类似与排序算法的归并算法,因此,总归并次数为N-1次。每次求连通分量时间复杂度O(V+E),空间复杂度O(V)。算法性能,非常依赖于图的划分,由于涉及到的是地图,道路通常是连接地理上相邻的点,因此,按照坐标区域即网格划分是适合的。(Graph partition,这是另外一个研究课题,参考文献丰富,如A FAST AND HIGH QUALITY MULTILEVEL SCHEME FOR PARTITIONING IRREGULAR GRAPHS GEORGE KARYPIS AND VIPIN KUMAR)
最坏情况下,整个网络,是一个无环有向图(DAG),或者每次划分都不能有效的缩减求解规模。
4. 实际测试结果分析
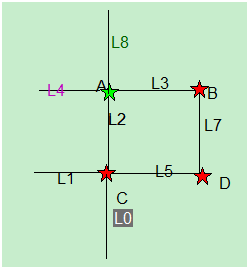
在真实的地图中,道路图,是一个条件有向图,不能使用通常的G=(V,E)来表示。举例如下, L1经过C点,可通过L2到达L8,但是不能同L2到达L4,但是L0可经过点C,通过L2,左转到L4也可以直行到L8。
此时<L1,L2,L4>构成一个禁止转向边——条件边,它不同于相邻边的拓扑关系描述,如简单的静止左转或者右转,如图中L2到L4,是可以通过对偶图来去掉条件边的。对偶图转换,简单的看,是把原图中的边当成新图中顶点,原图中边与边的关系,作为新图中的边。
还有属性边,比如限重门,限宽、高门,时间域等。但这些与设计的算法思路无关。
以北京地图为例,15万个顶点,17万条边,大约29s完成scc求解(包含结果作为文件输出)。