Minimum Spanning Tree

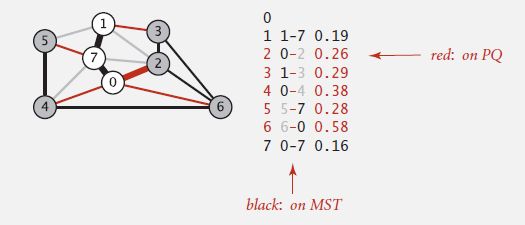
1.  Definition: Given an undirected graph G with positive edge weights (connected). A spanning tree of G is a subgraph T that is connected and acyclic. A minimum spanning tree is a min weight spanning tree.

 

2.  Applications:

    --  Dithering

    --  Cluster analysis

    --  Max bottleneck paths.

    --  Real-time face verification.

    --  LDPC codes for error correction.

    --  Image registration with Renyi entropy.

    --  Find road networks in satellite and aerial imagery.

    --  Model locality of particle interactions in turbulent fluid flows.

    --  Reducing data storage in sequencing amino acids in a protein.

    --  Autoconfig protocol for Ethernet bridging to avoid cycles in a network.

    --  Network design (communication, electrical, hydraulic, computer, road).

    --  Approximation algorithms for NP-hard problems (e.g., TSP, Steiner tree).

 

3.  Cut Property:

    --  A cut in a graph is a partition of its vertices into two (nonempty) sets.

    --  A crossing edge connects a vertex in one set with a vertex in the other.

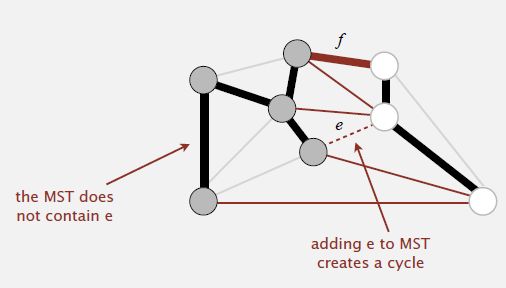
    --  Cut property. Given any cut, the crossing edge of min weight is in the MST.

    --  Pf. Suppose min-weight crossing edge e is not in the MST.

        a)  Adding e to the MST creates a cycle.

        b)  Some other edge f in cycle must be a crossing edge.

        c)  Removing f and adding e is also a spanning tree.

        d)  Since weight of e is less than the weight of f, that spanning tree is lower weight.

 

4.  Greedy MST algorithm:

    --  Start with all edges colored gray.

    --  Find cut with no black crossing edges; color its min-weight edge black.

    --  Repeat until V - 1 edges are colored black.

      Pf.

    --  Any edge colored black is in the MST (via cut property).

    -- Fewer than V - 1 black edges ⇒ cut with no black crossing edges.

    (consider cut whose vertices are one connected component)

 

5.  Weighted edge API

 

public class Edge implements Comparable<Edge>
{
    private final int v, w;
    private final double weight;
    public Edge(int v, int w, double weight)
    {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }
    public int either()
    { return v; }
    public int other(int vertex)
    {
        if (vertex == v) return w;
        else return v;
    }
    public int compareTo(Edge that)
    {
        if (this.weight < that.weight) return -1;
        else if (this.weight > that.weight) return +1;
        else return 0;
    }
    public double weight() {
        return this.weight
    }
    public String toString() {
        return this.v + "-" + this.w;
    }
}

 

 

6.  Edge-weighted graph: adjacency-lists implementation

 

public class EdgeWeightedGraph
{
    private final int V;
    private final Bag<Edge>[] adj;
    
    public EdgeWeightedGraph(int V)
    {
        this.V = V;
        adj = (Bag<Edge>[]) new Bag[V];
        for (int v = 0; v < V; v++)
            adj[v] = new Bag<Edge>();
    }
    public void addEdge(Edge e)
    {
        int v = e.either(), w = e.other(v);
        adj[v].add(e);
        adj[w].add(e);
    }
    public Iterable<Edge> adj(int v)
    {  
        return adj[v]; 
    }
    Iterable<Edge> edges() {}  //all edges in this graph
    int V() {}  //number of vertices
    int E() {}  //number of edges
    String toString() {} //string representation
}

 

7.  Minimum spanning tree API:

 

public class MST {
    public MST(EdgeWeightedGraph G) {} //constructor
    
    public Iterable<Edge> edges() {} //edges in MST
  
    double weight() {} //weight of MST
}

 

 

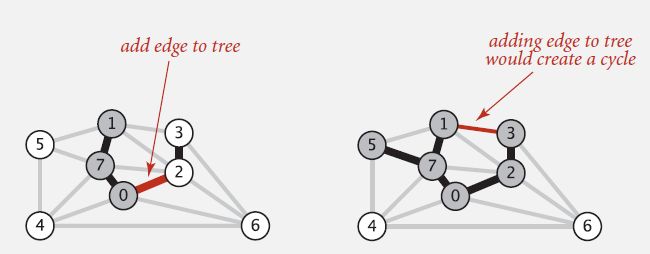
8.  Kruskal's algorithm:

    -- Algorithm :

        a)  Consider edges in ascending order of weight.

        b)  Add next edge to tree T unless doing so would create a cycle.

    --  Pf. Kruskal's algorithm is a special case of the greedy MST algorithm.

        a)  Suppose Kruskal's algorithm colors the edge e = v–w black.

        b)  Cut = set of vertices connected to v in tree T.

        c)  No crossing edge is black.

        d)  No crossing edge has lower weight.

    --  Implementation challenge :

        Would adding edge v–w to tree T create a cycle? If not, add it.

    --  Efficient solution. Use the union-find data structure:

        a)  Maintain a set for each connected component in T.

        b)  if v and w are in same set, then adding v–w would create a cycle.

        c)  To add v–w to T, merge sets containing v and w.

    --  Java Implementation :

 

public class KruskalMST
{
    private Queue<Edge> mst = new Queue<Edge>();
    public KruskalMST(EdgeWeightedGraph G)
    {
        MinPQ<Edge> pq = new MinPQ<Edge>();
        for (Edge e : G.edges())
            pq.insert(e);
        UF uf = new UF(G.V());
        while (!pq.isEmpty() && mst.size() < G.V()-1)
        {
            Edge e = pq.delMin();
            int v = e.either(), w = e.other(v);
            if (!uf.connected(v, w))
            {
                uf.union(v, w);
                mst.enqueue(e);
             }
        }
    }
    public Iterable<Edge> edges()
    { return mst; }
}

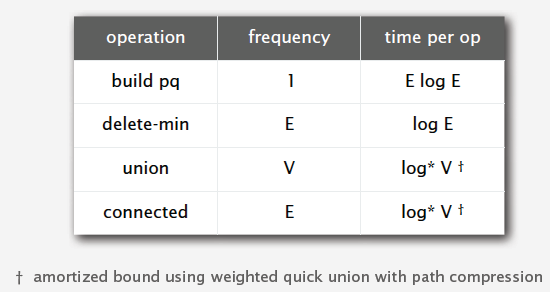
     --  Running Time :

 

    Kruskal's algorithm computes MST in time proportional to E log E (in the worst case).

 

9.  Prim's algorithm:

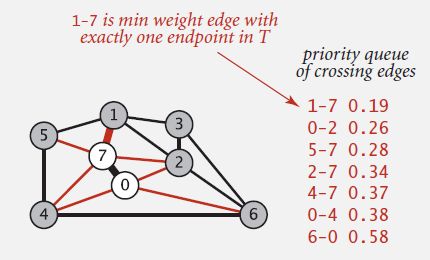
    -- Algorithm

        a)  Start with vertex 0 and greedily grow tree T.

        b)  Add to T the min weight edge with exactly one endpoint in T.

        c)  Repeat until V - 1 edges.

    --  Pf. Prim's algorithm is a special case of the greedy MST algorithm.

        a)  Suppose edge e = min weight edge connecting a vertex on the tree to a vertex not on the tree.

        b)  Cut = set of vertices connected on tree.

        c)  No crossing edge is black.

        d)  No crossing edge has lower weight.

    --  Challenge. Find the min weight edge with exactly one endpoint in T.

    --  Lazy solution: Maintain a PQ of edges with (at least) one endpoint in T.

        a)  Key = edge; priority = weight of edge.

        b)  Delete-min to determine next edge e = v–w to add to T.

        c)  Disregard if both endpoints v and w are in T.

        d)  Otherwise, let w be the vertex not in T :

            – add to PQ any edge incident to w (assuming other endpoint not in T)

            – add w to T

     --  Java Implementation

 

public class LazyPrimMST
{
    private boolean[] marked; // MST vertices
    private Queue<Edge> mst; // MST edges
    private MinPQ<Edge> pq; // PQ of edges
    public LazyPrimMST(WeightedGraph G)
    {
        pq = new MinPQ<Edge>();
        mst = new Queue<Edge>();
        marked = new boolean[G.V()];
        visit(G, 0);
        while (!pq.isEmpty() && mst.size() < G.V() - 1)
        {
            Edge e = pq.delMin();
            int v = e.either(), w = e.other(v);
            if (marked[v] && marked[w]) continue;
            mst.enqueue(e);
            if (!marked[v]) visit(G, v);
            if (!marked[w]) visit(G, w);
        }
    }
    
    private void visit(WeightedGraph G, int v)
    {
        marked[v] = true;
        for (Edge e : G.adj(v))
            if (!marked[e.other(v)])
                pq.insert(e);
    }
    
    public Iterable<Edge> mst()
    { return mst; }
}

     --  Running Time

 

        Lazy Prim's algorithm computes the MST in time proportional to E log E and extra space proportional to E (in the worst case).

    
     --  Eager solution: Maintain a PQ of vertices connected by an edge to T

        a)  where priority of vertex v = weight of shortest edge connecting v to T.

        b)  Delete min vertex v and add its associated edge e = v–w to T.

        c)  Update PQ by considering all edges e = v–x incident to v

            – ignore if x is already in T

            – add x to PQ if not already on it

            – decrease priority of x if v–x becomes shortest edge connecting x to T

 
     --  Indexed priority queue

    Associate an index between 0 and N - 1 with each key in a priority queue.

        - Client can insert and delete-the-minimum.

        - Client can change the key by specifying the index.

 

public class IndexMinPQ<Key extends Comparable<Key>> {

    IndexMinPQ(int N) {} //create indexed priority queue with indices 0, 1, …, N-1
    void insert(int i, Key key) {} //associate key with index i
    void decreaseKey(int i, Key key) {} //decrease the key associated with index i
    boolean contains(int i) {} //is i an index on the priority queue?
    int delMin() {} //remove a minimal key and return its associated index
    boolean isEmpty() {} //is the priority queue empty?
    int size() {} //number of entries in the priority queue
}

    --  Indexed Priority Queue Implementation:

 

        a)  Start with same code as MinPQ.

        b)  Maintain parallel arrays keys[], pq[], and qp[] so that:

            – keys[i] is the priority of i

            – pq[i] is the index of the key in heap position i

            – qp[i] is the heap position of the key with index i

         c)  Use swim(qp[i]) implement decreaseKey(i, key)

 

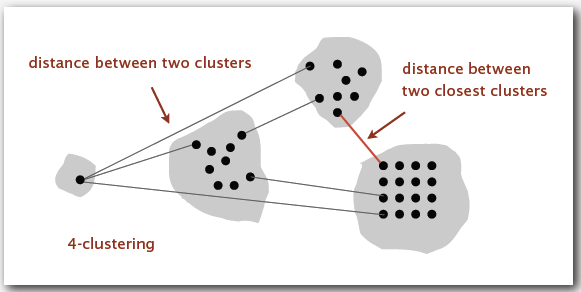
10.  Single-link clustering

    --  k-clustering. Divide a set of objects classify into k coherent groups.

    --  Distance function. Numeric value specifying "closeness" of two objects.

    --  Single link. Distance between two clusters equals the distance between the two closest objects (one in each cluster).

    --  Single-link clustering. Given an integer k, find a k-clustering that maximizes the distance between two closest clusters.

    --  Solution: Kruskal's algorithm stopping when k connected components:

        1)  Form V clusters of one object each.

        2)  Find the closest pair of objects such that each object is in a different cluster, and merge the two clusters.

        3)  Repeat until there are exactly k clusters.

    --  Alternate solution. Run Prim's algorithm and delete k-1 max weight edges.