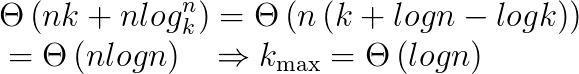归并排序（merge sorts）算法大串讲
归并排序（merge sorts）算法大串讲
本文内容框架：
§1 归并排序（Merge Sort）
§2 归并排序算法改进和优化
§3 Strand Sort排序
§4 小结
§1 归并排序（Merge Sort）
归并排序（Merge Sort）算法
归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
归并排序，它采取分而治之（Divide-and-Conquer）的策略，时间复杂度是Θ(nlgn)。归并排序的步骤如下：
1. Divide: 把长度为n的输入序列分成两个长度为n/2的子序列。
2. Conquer: 对这两个子序列分别采用归并排序。
3. Combine: 将两个排序好的子序列合并成一个最终的排序序列。
在描述归并排序的步骤时又调用了归并排序本身，可见这是一个递归的过程。
下面给出归并排序的递归和迭代两个版本实现
递归版本
//将有二个有序数列a[first...mid]和a[mid...last]合并。
void mergearray(int a[], int first, int mid, int last, int temp[])
{
int i = first, j = mid + 1;
int m = mid, n = last;
int k = 0;
while (i <= m && j <= n)
{
if (a[i] < a[j])
temp[k++] = a[i++];
else
temp[k++] = a[j++];
}
while (i <= m)
temp[k++] = a[i++];
while (j <= n)
temp[k++] = a[j++];
for (i = 0; i < k; i++)
a[first + i] = temp[i];
}
void mergesort(int a[], int first, int last, int temp[])
{
if (first < last)
{
int mid = (first + last) / 2;
mergesort(a, first, mid, temp); //左边有序
mergesort(a, mid + 1, last, temp); //右边有序
mergearray(a, first, mid, last, temp); //再将二个有序数列合并
}
}
bool MergeSort(int a[], int n)
{
int *p = new int[n];
if (p == NULL)
return false;
mergesort(a, 0, n - 1, p);
delete[] p;
return true;
}
不使用递归，使用迭代版本
void merge_sort(int *list, int length){
int i, left_min, left_max, right_min, right_max, next;
int *tmp = (int*)malloc(sizeof(int) * length);
if (tmp == NULL){
fputs("Error: out of memory\n", stderr);
abort();
}
for (i = 1; i < length; i *= 2)
for (left_min = 0; left_min < length - i; left_min = right_max){
right_min = left_max = left_min + i;
right_max = left_max + i;
if (right_max > length)
right_max = length;
next = 0;
while (left_min < left_max && right_min < right_max)
tmp[next++] = list[left_min] > list[right_min] ? list[right_min++] : list[left_min++];
while (left_min < left_max)
list[--right_min] = list[--left_max];
while (next > 0)
list[--right_min] = tmp[--next];
}
free(tmp);
}
比较操作的次数介于和。 赋值操作的次数是。 归并算法的空间复杂度为：Θ (n)
§2 归并排序算法改进和优化
归并排序算法改进
1.利用插入排序优化归并排序
在归并中利用插入排序不仅可以减少递归次数，还可以减少内存分配次数（针对于原始版本）。
尽管合并排序最坏情况运行时间为o(nlgn)，插入排序的最坏运行时间为o(n^2)，但是插入排序的常数因子使得它在n较小时，运行要更快一些。因此，在合并排序算法中，当子问题足够小时，采用插入排序就比较合适了。考虑对合并排序做这样的修改，即采用插入排序策略，对n/k个长度为k的子列表进行排序。然后，再用标准的合并机制将它们合并起来，此处k是一个待定的值。
a) 证明在最坏的情况下，n/k个子列表可以用插入排序在o(nk)的时间内完成排序
解答：每个列表长度为k，因此采用插入排序o(k^2)复杂度。因此k^2*n/k=kn
b) 证明这些子列表可以在o(nlg(n/k))最坏情况内完成合并。
c) 如果已知修改后的合并排序算法的最坏运行时间为o(nk+nlg(n/k)),要使得修改后的算法具有与标准合并算法一样的渐进运行时间，k的最大渐进形式是什么？
d) 实践中，应该如何选取k值。K=o(lgn)
解答：在实践中，k应该是使得插入排序比归并排序快的最大列表长度。
2.不回写+非递归优化归并排序
1）不回写：因为这样可以减少移动的次数，最简单的归并排序，每次对每两个有序表进行合并的时候都要保存到另外一个数组当中比如B【】数组，合并完之后要回写到原来的数组当中比如A【】。优化：我们可以这么做，比如当奇数次合并的时候是从A[]数组到B[]数组，偶数次是从B[]数组到A[]数组。这样可以减少一半的数据移动的次数
2）不递归：大家应该都知道，在进行递归调用的时候，需要对函数调用进行压栈出栈的操作，是非常的耗时间的，所以我们采用迭代法来代替递归对其进行改进，可以提高程序的性能。
#include <iostream>
using namespace std;
int data[10]={8,7,2,6,9,10,3,4,5,1};
int cp[10];
void Merge(int a[],int b[],int first,int mid,int last) //合并两个有序序列
{
int p=first,q=mid+1;
int pos=first;
while(p<=mid&&q<=last)
{
if(a[p]<a[q])
{
b[pos++]=a[p++];
}
else
{
b[pos++]=a[q++];
}
}
if(p>mid)
{
while(q<=last)
{
b[pos++]=a[q++];
}
}
else
{
while(p<=mid)
{
b[pos++]=a[p++];
}
}
}
void MergePass(int a[],int b[],int gap,int n) //以一定的步长对数据进行合并
{
int i=0;
int j;
while(i<=n-2*gap+1)
{
Merge(a,b,i,i+gap-1,i+2*gap-1);
i=i+2*gap;
}
if(i<(n-gap))
Merge(a,b,i,i+gap-1,n-1);
else
for(j=i;j<n;j++)
b[j]=a[j];
}
void Merge_sort(int a[],int b[],int n) //归并排序的非递归 并且不进行回写
{
int gap=1;
while(gap<n)
{
MergePass(a,b,gap,n);
gap=2*gap;
MergePass(b,a,gap,n);
gap=2*gap;
}
}
int main()
{
Merge_sort(data,cp,10);
for(int i=0;i<=9;i++)
cout<<data[i]<<endl;
system("pause");
return 0;
}
3.利用自然合并排序优化归并排序
该排序需要一个叫做pass()的子函数，该函数通过一次扫描，将排序前数组中已经有序的子数组段信息记录在rec[]数组中，然后返回原数组中自然序列的个数。
// 自然归并是归并排序的一个变形，效率更高一些，可以在归并排序非递归实现的基础上进行修改
//对于已经一个已经给定数组a,通常存在多个长度大于1的已经自然排好的子数组段
//因此用一次对数组a的线性扫描就可以找出所有这些排好序的子数组段
//然后再对这些子数组段俩俩合并
//代码的实现如下：
#include<iostream>
using namespace std;
const int SIZE = 100;
int arr[SIZE];
int rec[SIZE];//记录每个子串的起始坐标
//排序数组arr[fir:end]
//合并操作的子函数
void merge(int fir,int end,int mid);
//扫描得到子串的子函数
int pass(int n);
//自然合并函数
void mergeSort3(int n);
/********************************************************************/
void mergeSort3(int n){
int num=pass(n);
while(num!=2){
//num=2说明已经排好序了
//每循环一次，进行一次pass()操作
for(int i=0;i<num;i+=2)
//坐标解释可参加P23页的图示
merge(rec[i],rec[i+2]-1,rec[i+1]-1);
num=pass(n);
}
}
void merge(int fir,int end,int mid){
//合并
int tempArr[SIZE];
int fir1=fir,fir2=mid+1;
for(int i=fir;i<=end;i++){
if(fir1>mid)
tempArr[i]=arr[fir2++];
else if(fir2>end)
tempArr[i]=arr[fir1++];
else if(arr[fir1]>arr[fir2])
tempArr[i]=arr[fir2++];
else
tempArr[i]=arr[fir1++];
}
for(int i=fir;i<=end;i++)
arr[i]=tempArr[i];
}
int pass(int n){
int num=0;
int biger=arr[0];
rec[num++]=0;
for(int i=1;i<n;i++){
if(arr[i]>=biger)biger=arr[i];
else {
rec[num++]=i;
biger=arr[i];
}
}
//给rec[]加一个尾巴，方便排序
rec[num++]=n;
return num;
}
int main(){
int n;
while(cin>>n){
for(int i=0;i<n;i++)cin>>arr[i];
//测试mergeSort函数
/**/mergeSort3(n);
for(int i=0;i<n;i++)cout<<arr[i]<<" ";
cout<<endl;
//测试pass函数
/*int num = pass(n);
for(int i=0;i<num;i++)cout<<rec[i]<<" ";
cout<<endl;*/
}
return 0;
}
4.双向自然合并排序优化归并排序算法
这个算法在上一个优化算法的基础上改进的，就是同时记录逆序的子数组，并进行将其转换为升序来处理。
Strand Sort算法
Strand Sort算法的思想：需要一个空的数组用来存放最终的输出结果,给它取个名字叫"有序数组"，然后每次遍历待排数组,得到一个"子有序数组",然后将"子有序数组"与"有序数组"合并排序。
The strand sort algorithm is O(n^2) in the average case. In the best case (a list which is already sorted) the algorithm is linear, or O(n). In the worst case (a list which is sorted in reverse order) the algorithm is O(n^2).
Strand sort is most useful for data which is stored in a linked list, due to the frequent insertions and removals of data. Using another data structure, such as an array, would greatly increase the running time and complexity of the algorithm due to lengthy insertions and deletions. Strand sort is also useful for data which already has large amounts of sorted data, because such data can be removed in a single strand.
§3 Strand Sort排序
Strand Sort算法举例
| 3 1 5 4 2 | ||
| 1 4 2 | 3 5 | |
| 1 4 2 | 3 5 | |
| 2 | 1 4 | 3 5 |
| 2 | 1 3 4 5 | |
| 2 | 1 3 4 5 | |
| 1 2 3 4 5 |
待排数组[ 6 2 4 1 5 9 ]
第一趟遍历得到"子有序数组"[ 6 9],并将其归并排序到有序数组里
待排数组[ 2 4 1 5]
有序数组[ 6 9 ]
第二趟遍历再次得到"子有序数组"[2 4 5],将其归并排序到有序数组里
待排数组[ 1 ]
有序数组[ 2 4 5 6 9 ]
第三趟遍历再次得到"子有序数组"[ 1 ],将其归并排序到有序数组里
待排数组[]
有序数组[ 1 2 4 5 6 9 ]
待排数组为空,排序结束
Strand Sort算法步骤：
1.Parse the unsorted list once, taking out any ascending (sorted) numbers.
2.The (sorted) sublist is, for the first iteration, pushed onto the empty sorted list.
3.Parse the unsorted list again, again taking out relatively sorted numbers.
4.Since the sorted list is now populated, merge the sublist into the sorted list.
5.Repeat steps 3–4 until both the unsorted list and sublist are empty.
Strand Sort算法实现
#include <iostream>
using namespace std;
void merge(int res[],int resLen,int sublist[],int last)
{
int *temp = (int *)malloc(sizeof(int)*(resLen+last));
int beginRes=0;
int beginSublist=0;
int k;
for(k=0;beginRes<resLen && beginSublist<last;k++)
{
if(res[beginRes]<sublist[beginSublist])
temp[k]=res[beginRes++];
else temp[k]=sublist[beginSublist++];
//cout<<"k:"<<k<<" temp[k]:"<<temp[k]<<endl;
}
if(beginRes<resLen)
memcpy(temp+k,res+beginRes,(resLen-beginRes)*sizeof(int));
else if(beginSublist<last)
memcpy(temp+k,sublist+beginSublist,(last-beginSublist)*sizeof(int));
memcpy(res,temp,(resLen+last)*sizeof(int));
free(temp);
}
void strandSort(int array[],int length)
{
int *sublist=(int *)malloc(sizeof(int)*length);
int *res=(int *)malloc(sizeof(int)*length); //sizeof(array)=4
int i;
int resLen=0;
res[0]=array[0];
array[0]=0;
for(i=1;i<length;i++)
{
if(array[i]>res[resLen])
{
resLen++;
res[resLen]=array[i];
array[i]=0;
}
}
resLen++;
int last;
int times=1;
bool finished;
while (true)
{
finished = true;
last = -1;
for(i=times;i<length;i++)
{
//cout<<"This time array[i]: "<<array[i]<<endl;
if(array[i]!=0)
{
//cout<<"This time array[i]: "<<array[i]<<endl;
if (last==-1)
{
sublist[0]=array[i];
array[i]=0;
last=0;
finished = false;
}
else if(array[i]>sublist[last])
{
last++;
sublist[last]=array[i];
array[i]=0;
}
}
}
if(finished) break;
last++;
merge(res,resLen,sublist,last);
resLen=resLen+last;
times++;
}
memcpy(array,res,length*sizeof(int));
}
int main()
{
//int array[]={15,9,8,1,4,11,7,2,13,16,5,3,6,2,10,14};
int array[]={13,14,94,33,82,25,59,94,65,23,45,27,73,25,39,10,35,54,90,58};
int i;
int length=sizeof(array)/sizeof(int); //在这里 sizeof(array)=80
strandSort(array,length);
//int *arr = array;
//cout<<arr[2]<<endl;
for(i=0;i<length;i++)
{
cout<<array[i]<<" ";
}
cout<<endl;
return 0;
}
§4 小结
这篇博文列举了主要讲解了归并排序算法及其改进，基本可以掌握其中概要，管中窥豹，不求甚解。如果你有任何建议或者批评和补充，请留言指出，不胜感激，更多参考请移步互联网。
参考：
①MoreWindows： http://blog.csdn.net/morewindows/article/details/6678165
②hzami： http://blog.chinaunix.net/uid-27149258-id-3377329.html
③fangxia7： http://fangxia722.blog.163.com/blog/static/317290122009112831244671/
④icyfire0105： http://blog.csdn.net/icyfire0105/article/details/2066602
⑤glose： http://www.cnblogs.com/dlutxm/archive/2011/11/04/2236594.html
⑥六维空间： http://www.cnblogs.com/liushang0419/archive/2011/09/19/2181476.html
⑦tiantangrenjian： http://blog.csdn.net/tiantangrenjian/article/details/7172942
⑧更多参考来着维基百科