二分图匹配
二分图最大匹配的匈牙利算法
二分图是这样一个图,它的顶点可以分类两个集合X和Y,所有的边关联在两个顶点中,恰好一个属于集合X,另一个属于集合Y。
最大匹配: 图中包含边数最多的匹配称为图的最大匹配。
完美匹配: 如果所有点都在匹配边上,称这个最大匹配是完美匹配。
最小覆盖: 最小覆盖要求用最少的点(X集合或Y集合的都行)让每条边都至少和其中一个点关联。可以证明:最少的点(即覆盖数)=最大匹配数
最小路径覆盖:
用尽量少的不相交简单路径覆盖有向无环图G的所有结点。解决此类问题可以建立一个二分图模型。把所有顶点i拆成两个:X结点集中的i和Y结点集中的i',如果有边i->j,则在二分图中引入边i->j',设二分图最大匹配为m,则结果就是n-m。
最大独立集问题:
在N个点的图G中选出m个点,使这m个点两两之间没有边.求m最大值.
如果图G满足二分图条件,则可以用二分图匹配来做.最大独立集点数 = N - 最大匹配数
二分图最大匹配问题的匈牙利算法:
算法思想:
算法的思路是不停的找增广轨,并增加匹配的个数,增广轨顾名思义是指一条可以使匹配数变多的路径,在匹配问题中,增广轨的表现形式是一条"交错轨",也就是说这条由图的边组成的路径,它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且始点和终点还没有被选择过.这样交错进行,显然他有奇数条边.那么对于这样一条路径,我们可以将第一条边改为已匹配,第二条边改为未匹配...以此类推.也就是将所有的边进行"反色",容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对.另外,单独的一条连接两个未匹配点的边显然也是交错轨.可以证明,当不能再找到增广轨时,就得到了一个最大匹配.这也就是匈牙利算法的思路.
一、二分图最大匹配
二分图最大匹配的经典匈牙利算法是由Edmonds在1965年提出的,算法的核心就是根据一个初始匹配不停的找增广路,直到没有增广路为止。
匈牙利算法的本质实际上和基于增广路特性的最大流算法还是相似的,只需要注意两点:
(一)每个X节点都最多做一次增广路的起点;
(二)如果一个Y节点已经匹配了,那么增广路到这儿的时候唯一的路径是走到Y节点的匹配点(可以回忆最大流算法中的后向边,这个时候后向边是可以增流的)。
找增广路的时候既可以采用dfs也可以采用bfs,两者都可以保证O(nm)的复杂度,因为每找一条增广路的复杂度是O(m),而最多增广n次,dfs在实际实现中更加简短。
例子:如图
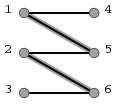
图1
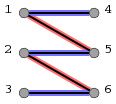
图2
图1是我给出的二分图中的一个匹配:[1,5]和[2,6]。图2就是在这个匹配的基础上找到的一条增广路径:3->6->2->5->1->4。我们借由它来描述一下二分图中的增广路径的性质:
(1)有奇数条边。
(2)起点在二分图的左半边,终点在右半边。
(3)路径上的点一定是一个在左半边,一个在右半边,交替出现。(其实二分图的性质就决定了这一点,因为二分图同一边的点之间没有边相连,不要忘记哦。)
(4)整条路径上没有重复的点。
(5)起点和终点都是目前还没有配对的点,而其它所有点都是已经配好对的。(如图1、图2所示,[1,5]和[2,6]在图1中是两对已经配好对的点;而起点3和终点4目前还没有与其它点配对。)
(6)路径上的所有第奇数条边都不在原匹配中,所有第偶数条边都出现在原匹配中。(如图1、图2所示,原有的匹配是[1,5]和[2,6],这两条配匹的边在图2给出的增广路径中分边是第2和第4条边。而增广路径的第1、3、5条边都没有出现在图1给出的匹配中。)
(7)最后,也是最重要的一条,把增广路径上的所有第奇数条边加入到原匹配中去,并把增广路径中的所有第偶数条边从原匹配中删除(这个操作称为增广路径的取反),则新的匹配数就比原匹配数增加了1个。(如图2所示,新的匹配就是所有蓝色的边,而所有红色的边则从原匹配中删除。则新的匹配数为3。)
不难想通,在最初始时,还没有任何匹配时,图1中的两条灰色的边本身也是增广路径。因此在这张二分图中寻找最大配匹的过程可能如下:
(1)找到增广路径1->5,把它取反,则匹配数增加到1。
(2)找到增广路径2->6,把它取反,则匹配数增加到2。
(3)找到增广路径3->6->2->5->1->4,把它取反,则匹配数增加到3。
(4)再也找不到增广路径,结束。
当然,这只是一种可能的流程。也可能有别的找增广路径的顺序,或者找到不同的增广路径,最终的匹配方案也可能不一样。但是最大匹配数一定都是相同的。
对于增广路径还可以用一个递归的方法来描述。这个描述不一定最准确,但是它揭示了寻找增广路径的一般方法:
“从点A出发的增广路径”一定首先连向一个在原匹配中没有与点A配对的点B。如果点B在原匹配中没有与任何点配对,则它就是这条增广路径的终点;反之,如果点B已与点C配对,那么这条增广路径就是从A到B,再从B到C,再加上“从点C出发的增广路径”。并且,这条从C出发的增广路径中不能与前半部分的增广路径有重复的点。
比如图2中,我们要寻找一条从3出发的增广路径,要做以下3步:
(1)首先从3出发,它能连到的点只有6,而6在图1中已经与2配对,所以目前的增广路径就是3->6->2再加上从2出发的增广路径。
(2)从2出发,它能连到的不与前半部分路径重复的点只有5,而且5确实在原匹配中没有与2配对。所以从2连到5。但5在图1中已经与1配对,所以目前的增广路径为3->6->2->5->1再加上从1出发的增广路径。
(3)从1出发,能连到的不与自已配对并且不与前半部分路径重复的点只有4。因为4在图1中没有与任何点配对,所以它就是终点。所以最终的增广路径是3->6->2->5->1->4。
但是严格地说,以上过程中从2出发的增广路径(2->5->1->4)和从1出发的增广路径(1->4)并不是真正的增广路径。因为它们不符合前面讲过的增广路径的第5条性质,它们的起点都是已经配过对的点。我们在这里称它们为“增广路径”只是为了方便说明整个搜寻的过程。而这两条路径本身只能算是两个不为外界所知的子过程的返回结果。
显然,从上面的例子可以看出,搜寻增广路径的方法就是DFS,可以写成一个递归函数。当然,用BFS也完全可以实现。
二、Hopcroft-Karp算法
SRbGa很早就介绍过这个算法,它可以做到O(sqrt(n)*e)的时间复杂度,并且在实际使用中效果不错而且算法本身并不复杂。
Hopcroft-Karp算法是Hopcroft和Karp在1972年提出的,该算法的主要思想是在每次增广的时候不是找一条增广路而是同时找几条不相交的最短增广路,形成极大增广路集,随后可以沿着这几条增广路同时进行增广。
可以证明在寻找增广路集的每一个阶段所寻找到的最短增广路都具有相等的长度,并且随着算法的进行最短增广路的长度是越来越长的,更进一步的分析可以证明最多只需要增广ceil(sqrt(n))次就可以得到最大匹配(证明在这里略去)。
因此现在的主要难度就是在O(e)的时间复杂度内找到极大最短增广路集,思路并不复杂,首先从所有X的未盖点进行BFS,BFS之后对每个X节点和Y节点维护距离标号,如果Y节点是未盖点那么就找到了一条最短增广路,BFS完之后就找到了最短增广路集,随后可以直接用DFS对所有允许弧(dist[y]=dist[x]+1,可以参见高流推进HLPP的实现)进行类似于匈牙利中寻找增广路的操作,这样就可以做到O(m)的复杂度。
实现起来也并不复杂,对于两边各50000个点,200000条边的二分图最大匹配可以在1s内出解,效果很好:)
三、二分图最优匹配
二分图最优匹配的经典算法是由Kuhn和Munkres独立提出的KM算法,值得一提的是最初的KM算法是在1955年和1957年提出的,因此当时的KM算法是以矩阵为基础的,随着匈牙利算法被Edmonds提出之后,现有的KM算法利用匈牙利树可以得到更漂亮的实现。
KM算法中的基本概念是可行顶标(feasible vertex labeling),它是节点的实函数并且对于任意弧(x,y)满足l(x)+l(y)≥w(x,y),此外一个概念是相等子图,它是G的一个生成子图,但是只包含满足l(xi)+l(yj)=w(xi,yj)的所有弧(xi,yj)。
有定理:如果相等子图有完美匹配,那么该匹配是最大权匹配,证明非常直观也非常简单,反设其他匹配是最优匹配,它的权必然比相等子图的完美匹配的权要小。
KM算法主要就是控制了怎样修改可行顶标的策略使得最终可以达到一个完美匹配,首先任意设置可行顶标(如每个X节点的可行顶标设为它出发的所有弧的最大权,Y节点的可行顶标设为0),然后在相等子图中寻找增广路,找到增广路就沿着增广路增广。
而如果没有找到增广路呢,那么就考虑所有现在在匈牙利树中的X节点(记为S集合),所有现在在匈牙利树中的Y节点(记为T集合),考察所有一段在S集合,一段在not T集合中的弧,取
delta = min {l(xi)+l(yj)-w(xi,yj),xi ∈ S, yj ∈ not T}
明显的,当我们把所有S集合中的l(xi)减少delta之后,一定会有至少一条属于(S,not T)的边进入相等子图,进而可以继续扩展匈牙利树,为了保证原来属于(S,T)的边不退出相等子图,把所有在T集合中的点的可行顶标增加delta。
随后匈牙利树继续扩展,如果新加入匈牙利树的Y节点是未盖点,那么找到增广路,否则把该节点的对应的X匹配点加入匈牙利树继续尝试增广。
复杂度分析:由于在不扩大匹配的情况下每次匈牙利树做如上调整之后至少增加一个元素,因此最多执行n次就可以找到一条增广路,最多需要找n条增广路,故最多执行n^2次修改顶标的操作,而每次修改顶标需要扫描所有弧,这样修改顶标的复杂度就是O(n^2)的,总的复杂度是O(n^4)的。
事实上我现在看到的几个版本的实现都是这样实现的,但是实际效果还不错,因为这个界通常很难达到。
对于not T的每个元素yj,定义松弛变量slack(yj) = min{l(xi)+l(yj)-w(xi,yj),xi ∈ S},很明显的每次的delta=min{slack(yj),yj∈ not T},每次增广之后用O(n^2)的时间计算所有点的初始slack,由于生长匈牙利树的时候每条弧的顶标增量相同,因此修改每个slack需要常数时间(注意在修改顶标后和把已盖Y节点对应的X节点加入匈牙利树的时候是需要修改slack的)。这样修改所有slack值时间是O(n)的,每次增广后最多修改n次顶标,那么修改顶标的总时间降为O(n^2),n次增广的总时间复杂度降为O(n^3)。事实上我这样实现之后对于大部分的数据可以比O(n^4)的算法快一倍左右。
四、二分图的相关性质
本部分内容主要来自于SRbGa的黑书,因为比较简单,仅作提示性叙述。
(1) 二分图的最大匹配数等于最小覆盖数,即求最少的点使得每条边都至少和其中的一个点相关联,很显然直接取最大匹配的一段节点即可。
(2) 二分图的独立数等于顶点数减去最大匹配数,很显然的把最大匹配两端的点都从顶点集中去掉这个时候剩余的点是独立集,这是|V|-2*|M|,同时必然可以从每条匹配边的两端取一个点加入独立集并且保持其独立集性质。
(3) DAG的最小路径覆盖,将每个点拆点后作最大匹配,结果为n-m,求具体路径的时候顺着匹配边走就可以,匹配边i→j',j→k',k→l'....构成一条有向路径。
【最优完备匹配】
对于二分图的每条边都有一个权(非负),要求一种完备匹配方案,使得所有匹配边的权和最大,记做最优完备匹配。(特殊的,当所有边的权为1时,就是最大完备匹配问题)
KM算法:(全称是Kuhn-Munkras,是这两个人在1957年提出的,有趣的是,匈牙利算法是在1965年提出的)
为每个点设立一个顶标Li,先不要去管它的意义。
设vi,j 为(i,j)边的权,如果可以求得一个完备匹配,使得每条匹配边vi,j=Li+Lj,其余边vi,j≤Li+Lj。
此时的解就是最优的,因为匹配边的权和=∑Li,其余任意解的权和都不可能比这个大
定理:二分图中所有vi,j=Li+Lj的边构成一个子图G,用匈牙利算法求G中的最大匹配,如果该匹配是完备匹配,则是最优完备匹配。
问题是,现在连Li的意义还不清楚。
其实,我们现在要求的就是L的值,使得在该L值下达到最优完备匹配。
L初始化:
Li=max{wi,j}(i∈x,j∈y)
Lj=0
建立子图G,用匈牙利算法求G的最大匹配,如果在某点i (i∈x)找不到增广轨,则得不到完备匹配。
此时需要对L做一些调整:
设S为寻找从i出发的增广轨时访问的x中的点的集合,T为访问的y中的点的集合。
找到一个改进量dx,dx=min{Li+Lj-wi,j}(i∈S,j不∈T)
Li=Li-dx (i∈S)
Li=Li+dx (i∈T)
重复以上过程,不断的调整L,直到求出完备匹配为止。
从调整过程中可以看出:
每次调整后新子图中在包含原子图中所有的边的基础上添加了一些新边。
每次调整后∑Li会减少dx,由于每次dx取最小,所以保证了解的最优性。
复杂度分析:
设n为点数,m为边数,从每个点出发寻找增广轨的复杂度是O(m),如果找不到增广轨,对L做调整的复杂度也是O(m),而一次调整或者找到一条增广轨,或者将两个连通分量合成一个,而这两种情况最多都只进行O(n)次,所以总的复杂度是O(nm)
扩展:
根据KM算法的实质,可以求出使得所有匹配边的权和最小的匹配方案。
L初始化:
Li=min{wi,j}(i∈x,j∈y)
Lj=0
dx=min{wi,j-Li-Lj}(i∈S,j不∈T)
Li=Li+dx (i∈S)
Li=Li-dx (i∈T)
【最优匹配】
与最优完备匹配很相似,但不必以完备匹配为前提。
只要对KM算法作一些修改就可以了:
将原图转换成完全二分图(m=|x||y|),添加原图中不存在的边,并且设该边的权值为0。
二分图是这样一个图,它的顶点可以分类两个集合X和Y,所有的边关联在两个顶点中,恰好一个属于集合X,另一个属于集合Y。
最大匹配: 图中包含边数最多的匹配称为图的最大匹配。
完美匹配: 如果所有点都在匹配边上,称这个最大匹配是完美匹配。
最小覆盖: 最小覆盖要求用最少的点(X集合或Y集合的都行)让每条边都至少和其中一个点关联。可以证明:最少的点(即覆盖数)=最大匹配数
最小路径覆盖:
用尽量少的不相交简单路径覆盖有向无环图G的所有结点。解决此类问题可以建立一个二分图模型。把所有顶点i拆成两个:X结点集中的i和Y结点集中的i',如果有边i->j,则在二分图中引入边i->j',设二分图最大匹配为m,则结果就是n-m。
最大独立集问题:
在N个点的图G中选出m个点,使这m个点两两之间没有边.求m最大值.
如果图G满足二分图条件,则可以用二分图匹配来做.最大独立集点数 = N - 最大匹配数
二分图最大匹配问题的匈牙利算法:
#define N 202
int useif[N]; //记录y中节点是否使用
int link[N]; //记录当前与y节点相连的x的节点
int mat[N][N]; //记录连接x和y的边,如果i和j之间有边则为1,否则为0
int gn,gm; //二分图中x和y中点的数目
int can(int t)
{
int i;
for(i=1;i<=gm;i++)
{
if(useif[i]==0 && mat[t][i])
{
useif[i]=1;
if(link[i]==-1 || can(link[i]))
{
link[i]=t;
return 1;
}
}
}
return 0;
}
int MaxMatch()
{
int i,num;
num=0;
memset(link,0xff,sizeof(link));
for(i=1;i<=gn;i++)
{
memset(useif,0,sizeof(useif));
if(can(i)) num++;
}
return num;
}
算法思想:
算法的思路是不停的找增广轨,并增加匹配的个数,增广轨顾名思义是指一条可以使匹配数变多的路径,在匹配问题中,增广轨的表现形式是一条"交错轨",也就是说这条由图的边组成的路径,它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且始点和终点还没有被选择过.这样交错进行,显然他有奇数条边.那么对于这样一条路径,我们可以将第一条边改为已匹配,第二条边改为未匹配...以此类推.也就是将所有的边进行"反色",容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对.另外,单独的一条连接两个未匹配点的边显然也是交错轨.可以证明,当不能再找到增广轨时,就得到了一个最大匹配.这也就是匈牙利算法的思路.
一、二分图最大匹配
二分图最大匹配的经典匈牙利算法是由Edmonds在1965年提出的,算法的核心就是根据一个初始匹配不停的找增广路,直到没有增广路为止。
匈牙利算法的本质实际上和基于增广路特性的最大流算法还是相似的,只需要注意两点:
(一)每个X节点都最多做一次增广路的起点;
(二)如果一个Y节点已经匹配了,那么增广路到这儿的时候唯一的路径是走到Y节点的匹配点(可以回忆最大流算法中的后向边,这个时候后向边是可以增流的)。
找增广路的时候既可以采用dfs也可以采用bfs,两者都可以保证O(nm)的复杂度,因为每找一条增广路的复杂度是O(m),而最多增广n次,dfs在实际实现中更加简短。
例子:如图

图1

图2
图1是我给出的二分图中的一个匹配:[1,5]和[2,6]。图2就是在这个匹配的基础上找到的一条增广路径:3->6->2->5->1->4。我们借由它来描述一下二分图中的增广路径的性质:
(1)有奇数条边。
(2)起点在二分图的左半边,终点在右半边。
(3)路径上的点一定是一个在左半边,一个在右半边,交替出现。(其实二分图的性质就决定了这一点,因为二分图同一边的点之间没有边相连,不要忘记哦。)
(4)整条路径上没有重复的点。
(5)起点和终点都是目前还没有配对的点,而其它所有点都是已经配好对的。(如图1、图2所示,[1,5]和[2,6]在图1中是两对已经配好对的点;而起点3和终点4目前还没有与其它点配对。)
(6)路径上的所有第奇数条边都不在原匹配中,所有第偶数条边都出现在原匹配中。(如图1、图2所示,原有的匹配是[1,5]和[2,6],这两条配匹的边在图2给出的增广路径中分边是第2和第4条边。而增广路径的第1、3、5条边都没有出现在图1给出的匹配中。)
(7)最后,也是最重要的一条,把增广路径上的所有第奇数条边加入到原匹配中去,并把增广路径中的所有第偶数条边从原匹配中删除(这个操作称为增广路径的取反),则新的匹配数就比原匹配数增加了1个。(如图2所示,新的匹配就是所有蓝色的边,而所有红色的边则从原匹配中删除。则新的匹配数为3。)
不难想通,在最初始时,还没有任何匹配时,图1中的两条灰色的边本身也是增广路径。因此在这张二分图中寻找最大配匹的过程可能如下:
(1)找到增广路径1->5,把它取反,则匹配数增加到1。
(2)找到增广路径2->6,把它取反,则匹配数增加到2。
(3)找到增广路径3->6->2->5->1->4,把它取反,则匹配数增加到3。
(4)再也找不到增广路径,结束。
当然,这只是一种可能的流程。也可能有别的找增广路径的顺序,或者找到不同的增广路径,最终的匹配方案也可能不一样。但是最大匹配数一定都是相同的。
对于增广路径还可以用一个递归的方法来描述。这个描述不一定最准确,但是它揭示了寻找增广路径的一般方法:
“从点A出发的增广路径”一定首先连向一个在原匹配中没有与点A配对的点B。如果点B在原匹配中没有与任何点配对,则它就是这条增广路径的终点;反之,如果点B已与点C配对,那么这条增广路径就是从A到B,再从B到C,再加上“从点C出发的增广路径”。并且,这条从C出发的增广路径中不能与前半部分的增广路径有重复的点。
比如图2中,我们要寻找一条从3出发的增广路径,要做以下3步:
(1)首先从3出发,它能连到的点只有6,而6在图1中已经与2配对,所以目前的增广路径就是3->6->2再加上从2出发的增广路径。
(2)从2出发,它能连到的不与前半部分路径重复的点只有5,而且5确实在原匹配中没有与2配对。所以从2连到5。但5在图1中已经与1配对,所以目前的增广路径为3->6->2->5->1再加上从1出发的增广路径。
(3)从1出发,能连到的不与自已配对并且不与前半部分路径重复的点只有4。因为4在图1中没有与任何点配对,所以它就是终点。所以最终的增广路径是3->6->2->5->1->4。
但是严格地说,以上过程中从2出发的增广路径(2->5->1->4)和从1出发的增广路径(1->4)并不是真正的增广路径。因为它们不符合前面讲过的增广路径的第5条性质,它们的起点都是已经配过对的点。我们在这里称它们为“增广路径”只是为了方便说明整个搜寻的过程。而这两条路径本身只能算是两个不为外界所知的子过程的返回结果。
显然,从上面的例子可以看出,搜寻增广路径的方法就是DFS,可以写成一个递归函数。当然,用BFS也完全可以实现。
二、Hopcroft-Karp算法
SRbGa很早就介绍过这个算法,它可以做到O(sqrt(n)*e)的时间复杂度,并且在实际使用中效果不错而且算法本身并不复杂。
Hopcroft-Karp算法是Hopcroft和Karp在1972年提出的,该算法的主要思想是在每次增广的时候不是找一条增广路而是同时找几条不相交的最短增广路,形成极大增广路集,随后可以沿着这几条增广路同时进行增广。
可以证明在寻找增广路集的每一个阶段所寻找到的最短增广路都具有相等的长度,并且随着算法的进行最短增广路的长度是越来越长的,更进一步的分析可以证明最多只需要增广ceil(sqrt(n))次就可以得到最大匹配(证明在这里略去)。
因此现在的主要难度就是在O(e)的时间复杂度内找到极大最短增广路集,思路并不复杂,首先从所有X的未盖点进行BFS,BFS之后对每个X节点和Y节点维护距离标号,如果Y节点是未盖点那么就找到了一条最短增广路,BFS完之后就找到了最短增广路集,随后可以直接用DFS对所有允许弧(dist[y]=dist[x]+1,可以参见高流推进HLPP的实现)进行类似于匈牙利中寻找增广路的操作,这样就可以做到O(m)的复杂度。
实现起来也并不复杂,对于两边各50000个点,200000条边的二分图最大匹配可以在1s内出解,效果很好:)
三、二分图最优匹配
二分图最优匹配的经典算法是由Kuhn和Munkres独立提出的KM算法,值得一提的是最初的KM算法是在1955年和1957年提出的,因此当时的KM算法是以矩阵为基础的,随着匈牙利算法被Edmonds提出之后,现有的KM算法利用匈牙利树可以得到更漂亮的实现。
KM算法中的基本概念是可行顶标(feasible vertex labeling),它是节点的实函数并且对于任意弧(x,y)满足l(x)+l(y)≥w(x,y),此外一个概念是相等子图,它是G的一个生成子图,但是只包含满足l(xi)+l(yj)=w(xi,yj)的所有弧(xi,yj)。
有定理:如果相等子图有完美匹配,那么该匹配是最大权匹配,证明非常直观也非常简单,反设其他匹配是最优匹配,它的权必然比相等子图的完美匹配的权要小。
KM算法主要就是控制了怎样修改可行顶标的策略使得最终可以达到一个完美匹配,首先任意设置可行顶标(如每个X节点的可行顶标设为它出发的所有弧的最大权,Y节点的可行顶标设为0),然后在相等子图中寻找增广路,找到增广路就沿着增广路增广。
而如果没有找到增广路呢,那么就考虑所有现在在匈牙利树中的X节点(记为S集合),所有现在在匈牙利树中的Y节点(记为T集合),考察所有一段在S集合,一段在not T集合中的弧,取
delta = min {l(xi)+l(yj)-w(xi,yj),xi ∈ S, yj ∈ not T}
明显的,当我们把所有S集合中的l(xi)减少delta之后,一定会有至少一条属于(S,not T)的边进入相等子图,进而可以继续扩展匈牙利树,为了保证原来属于(S,T)的边不退出相等子图,把所有在T集合中的点的可行顶标增加delta。
随后匈牙利树继续扩展,如果新加入匈牙利树的Y节点是未盖点,那么找到增广路,否则把该节点的对应的X匹配点加入匈牙利树继续尝试增广。
复杂度分析:由于在不扩大匹配的情况下每次匈牙利树做如上调整之后至少增加一个元素,因此最多执行n次就可以找到一条增广路,最多需要找n条增广路,故最多执行n^2次修改顶标的操作,而每次修改顶标需要扫描所有弧,这样修改顶标的复杂度就是O(n^2)的,总的复杂度是O(n^4)的。
事实上我现在看到的几个版本的实现都是这样实现的,但是实际效果还不错,因为这个界通常很难达到。
对于not T的每个元素yj,定义松弛变量slack(yj) = min{l(xi)+l(yj)-w(xi,yj),xi ∈ S},很明显的每次的delta=min{slack(yj),yj∈ not T},每次增广之后用O(n^2)的时间计算所有点的初始slack,由于生长匈牙利树的时候每条弧的顶标增量相同,因此修改每个slack需要常数时间(注意在修改顶标后和把已盖Y节点对应的X节点加入匈牙利树的时候是需要修改slack的)。这样修改所有slack值时间是O(n)的,每次增广后最多修改n次顶标,那么修改顶标的总时间降为O(n^2),n次增广的总时间复杂度降为O(n^3)。事实上我这样实现之后对于大部分的数据可以比O(n^4)的算法快一倍左右。
四、二分图的相关性质
本部分内容主要来自于SRbGa的黑书,因为比较简单,仅作提示性叙述。
(1) 二分图的最大匹配数等于最小覆盖数,即求最少的点使得每条边都至少和其中的一个点相关联,很显然直接取最大匹配的一段节点即可。
(2) 二分图的独立数等于顶点数减去最大匹配数,很显然的把最大匹配两端的点都从顶点集中去掉这个时候剩余的点是独立集,这是|V|-2*|M|,同时必然可以从每条匹配边的两端取一个点加入独立集并且保持其独立集性质。
(3) DAG的最小路径覆盖,将每个点拆点后作最大匹配,结果为n-m,求具体路径的时候顺着匹配边走就可以,匹配边i→j',j→k',k→l'....构成一条有向路径。
【最优完备匹配】
对于二分图的每条边都有一个权(非负),要求一种完备匹配方案,使得所有匹配边的权和最大,记做最优完备匹配。(特殊的,当所有边的权为1时,就是最大完备匹配问题)
KM算法:(全称是Kuhn-Munkras,是这两个人在1957年提出的,有趣的是,匈牙利算法是在1965年提出的)
为每个点设立一个顶标Li,先不要去管它的意义。
设vi,j 为(i,j)边的权,如果可以求得一个完备匹配,使得每条匹配边vi,j=Li+Lj,其余边vi,j≤Li+Lj。
此时的解就是最优的,因为匹配边的权和=∑Li,其余任意解的权和都不可能比这个大
定理:二分图中所有vi,j=Li+Lj的边构成一个子图G,用匈牙利算法求G中的最大匹配,如果该匹配是完备匹配,则是最优完备匹配。
问题是,现在连Li的意义还不清楚。
其实,我们现在要求的就是L的值,使得在该L值下达到最优完备匹配。
L初始化:
Li=max{wi,j}(i∈x,j∈y)
Lj=0
建立子图G,用匈牙利算法求G的最大匹配,如果在某点i (i∈x)找不到增广轨,则得不到完备匹配。
此时需要对L做一些调整:
设S为寻找从i出发的增广轨时访问的x中的点的集合,T为访问的y中的点的集合。
找到一个改进量dx,dx=min{Li+Lj-wi,j}(i∈S,j不∈T)
Li=Li-dx (i∈S)
Li=Li+dx (i∈T)
重复以上过程,不断的调整L,直到求出完备匹配为止。
从调整过程中可以看出:
每次调整后新子图中在包含原子图中所有的边的基础上添加了一些新边。
每次调整后∑Li会减少dx,由于每次dx取最小,所以保证了解的最优性。
复杂度分析:
设n为点数,m为边数,从每个点出发寻找增广轨的复杂度是O(m),如果找不到增广轨,对L做调整的复杂度也是O(m),而一次调整或者找到一条增广轨,或者将两个连通分量合成一个,而这两种情况最多都只进行O(n)次,所以总的复杂度是O(nm)
扩展:
根据KM算法的实质,可以求出使得所有匹配边的权和最小的匹配方案。
L初始化:
Li=min{wi,j}(i∈x,j∈y)
Lj=0
dx=min{wi,j-Li-Lj}(i∈S,j不∈T)
Li=Li+dx (i∈S)
Li=Li-dx (i∈T)
【最优匹配】
与最优完备匹配很相似,但不必以完备匹配为前提。
只要对KM算法作一些修改就可以了:
将原图转换成完全二分图(m=|x||y|),添加原图中不存在的边,并且设该边的权值为0。