排序算法
排序方法
包括方法是插入排序,归并排序,通用排序,快速排序,第K大元素查找
1.0插入排序
老师在返回试卷给学生之前会,把试卷按学生的名字的字母顺序排序,现在老师要排序的学生的卷子有:Monroe,chin,Flores,Stein,Dare
如图
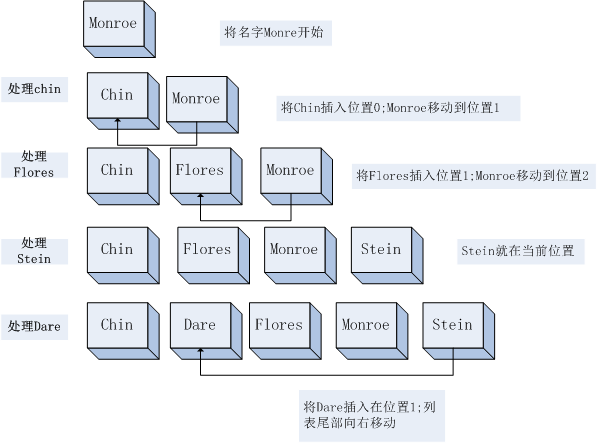
1.1插入原理
1.2测试用例
2.0分治排序算法
分解: 将元素分隔成长度相等的两个数组.
递归求解: 将每对已排序的组合为一个大的已排序的列表
分治策略是归并排序, 通过在中性点进行分离, 归并精确对半分隔元素.递归列表分为两个部分,每个部分都含有二分之一的元素;随后将这两个部分再分解为四个部分, 每个部分都含有4分之一的元素,以此类推. 主要子列表具有两个以上或多个元素, 这个分解过程就会继续进行下去.以相反的顺序执行组合时,递归步骤会将一排序的部分列表部分和并越来越大的有序列表,直到算法以升序重够了原始序列
2.1归并排序
一个数组整数int[] arr={7,10,19,25,12,17,21,30,48}现在以归并排序为例
步骤1: 比较arr[indexA]=7与arr[indexB]=12.将较小的元素7复制到数组tempArr的索引indexC处.indexA++;indexC++;
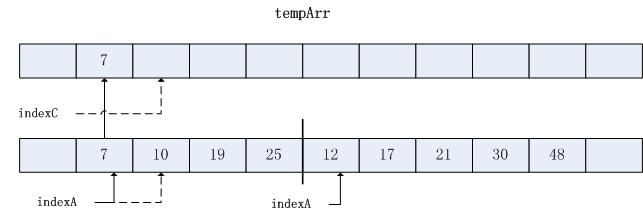
步骤2:比较arr[indexA]=10与arr[indexB]=12.将较小的元素10复制到数组tempArr的索引indexC处.

步骤3:比较arr[indexA]=19与arr[indexB]=12.将较小的元素12复制到数组tempArr的索引indexC处.

步骤4~7:对两个子列表中元素的成对比较继续将元素17,19,21和25复制到数组tempArr.此时, indexA到子列表A的末尾(indexA==mid),indexB引用的值为30
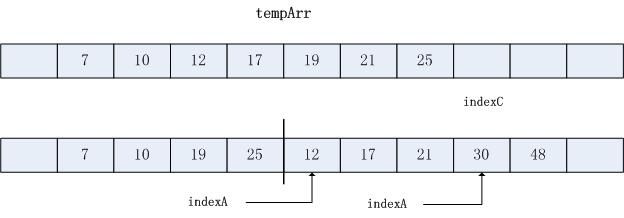
步骤8~9: 合并过程通常选择完一个列表, 另外一个列表的尾部则还为选中.在这个示例子中,子列表b尾部中元素30和48还未负责到tempArr.步骤8和9子列表B的尾部复制到tempArr, 直到indexB到达末尾(indexB==last)
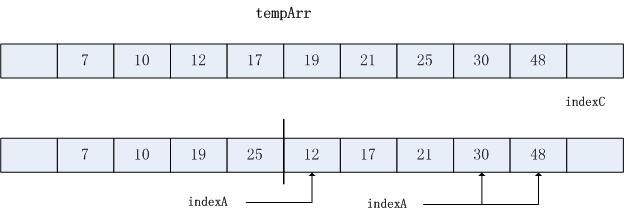
2.1归并排序原理
int mid=(first+last)/2;
每个递归步骤都会生成对于mergeSort()方法的两个调用.其中一个调用使用索引first和mid来的定义用于原始序列下半部分列表的索引范围[first,mid);第二个调用是使用索引mid和last用于原始序列的上半部分的索引范围[mid,last).这个过程可以生成一个递归调用链,从而将原始序列分隔为越来越小的子列表, 直到这些子列表的长度变为1(停止条件).长度为1的显然已经排好序.然后以相反顺序重新访问递归调用链使用合并算法构建越来越大的有序子列表.
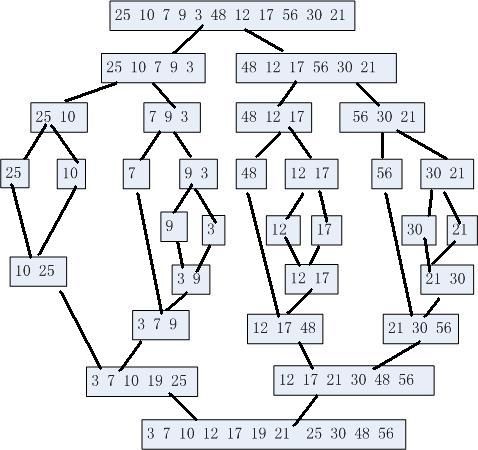
2.2测试用例
3.0快速排序
快速排序使用一些列递归调用算法将列表分割为若干越来越小的子列表, 这些子列表位于基准值(pivot)左右. 每个递归步骤根据作为列表中心的点值的基准进行选择.分割算法完成交换, 从而使基准值在元素排序后被放置在列表中的正确位置上.此时,下子列表只含小于或等于表准值的元素, 而上字表只含大于或等于基准值的元素.
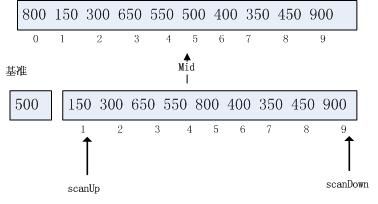
scanUp继续向上搜索,在索引3处,scanDown停止在索引8处
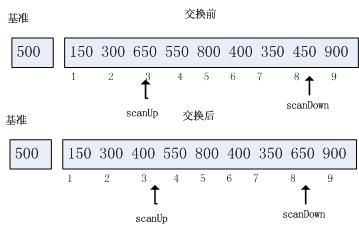
继续上面的步骤,到达停止条件
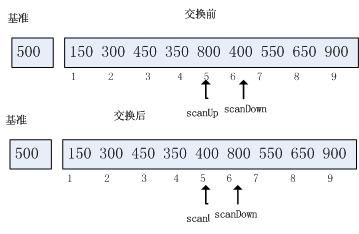
在scanDown<=scanUp时,分割过程终止.如果scanDown==scanUp,那么arr[scanDown]<=pivot并且arr[scanUp>=pivot

3.2快速排序
递归调用链
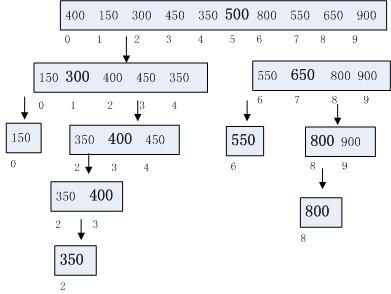
3.3 快速排序查找基准值
包括方法是插入排序,归并排序,通用排序,快速排序,第K大元素查找
1.0插入排序
老师在返回试卷给学生之前会,把试卷按学生的名字的字母顺序排序,现在老师要排序的学生的卷子有:Monroe,chin,Flores,Stein,Dare
如图

1.1插入原理
引用
假定n是数组arr的长度.排序关系假定第一个元素被放置到其正确的位置上, 这样需要从1到n-1方位内的n-1个遍对剩余元素进行排序. 对于通用的遍i来说,从0到i-1范围内的元素已i的子列表之内的正确位置上.将arr[i]复制为一个名为target的临时元素.向下扫描列表,比较这个目标值与项arr[i-1],arr[i-2],依次类推.
/**
* 插入排序:插入排序算法在已排列子列表中插入
* @param <T>
* @param arr
*/
public static <T extends Comparable<? super T>> void insertionSort(T[] arr) {
int n = arr.length;
T target;
for (int i = 1; i < n; i++) {
target = arr[i];
int j = i;
while (j > 0 && target.compareTo(arr[j - 1]) < 0) {//i元素找到0到i-1小于i的元素
arr[j] = arr[j - 1];//前后交换
j--;
}
arr[j] = target;
}
}
1.2测试用例
/**
* 测试: 插入排序
*/
public void insertionSort() {
Integer[] intArr = { 2, 5, 3, 5, 4, 7, 5, 1, 8, 9 };
ArraysUtil.printArrays(intArr);//把数组输出到控制台,此类在附件能找到
Arrays.insertionSort(intArr);//Arrays类里面插入排序方法
ArraysUtil.printArrays(intArr);
}
2.0分治排序算法
分解: 将元素分隔成长度相等的两个数组.
递归求解: 将每对已排序的组合为一个大的已排序的列表
分治策略是归并排序, 通过在中性点进行分离, 归并精确对半分隔元素.递归列表分为两个部分,每个部分都含有二分之一的元素;随后将这两个部分再分解为四个部分, 每个部分都含有4分之一的元素,以此类推. 主要子列表具有两个以上或多个元素, 这个分解过程就会继续进行下去.以相反的顺序执行组合时,递归步骤会将一排序的部分列表部分和并越来越大的有序列表,直到算法以升序重够了原始序列
2.1归并排序
一个数组整数int[] arr={7,10,19,25,12,17,21,30,48}现在以归并排序为例
步骤1: 比较arr[indexA]=7与arr[indexB]=12.将较小的元素7复制到数组tempArr的索引indexC处.indexA++;indexC++;

步骤2:比较arr[indexA]=10与arr[indexB]=12.将较小的元素10复制到数组tempArr的索引indexC处.

步骤3:比较arr[indexA]=19与arr[indexB]=12.将较小的元素12复制到数组tempArr的索引indexC处.

步骤4~7:对两个子列表中元素的成对比较继续将元素17,19,21和25复制到数组tempArr.此时, indexA到子列表A的末尾(indexA==mid),indexB引用的值为30

步骤8~9: 合并过程通常选择完一个列表, 另外一个列表的尾部则还为选中.在这个示例子中,子列表b尾部中元素30和48还未负责到tempArr.步骤8和9子列表B的尾部复制到tempArr, 直到indexB到达末尾(indexB==last)

2.1归并排序原理
引用
int mid=(first+last)/2;
每个递归步骤都会生成对于mergeSort()方法的两个调用.其中一个调用使用索引first和mid来的定义用于原始序列下半部分列表的索引范围[first,mid);第二个调用是使用索引mid和last用于原始序列的上半部分的索引范围[mid,last).这个过程可以生成一个递归调用链,从而将原始序列分隔为越来越小的子列表, 直到这些子列表的长度变为1(停止条件).长度为1的显然已经排好序.然后以相反顺序重新访问递归调用链使用合并算法构建越来越大的有序子列表.

public static <T extends Comparable<? super T>> void msort(T[] arr,
T[] tempArr, int first, int last) {
if (first + 1 < last) {
int midpt = (last + first) / 2;
msort(arr, tempArr, first, midpt);
msort(arr, tempArr, midpt, last);
if (arr[midpt - 1].compareTo(arr[midpt]) <= 0)
return;
int indexA, indexB, indexC;
indexA = first;
indexB = midpt;
indexC = first;
while (indexA < midpt && indexB < last) {
if (arr[indexA].compareTo(arr[indexB]) < 0) {
tempArr[indexC] = arr[indexA]; // copy element to tempArr
indexA++; // increment indexA
} else {
tempArr[indexC] = arr[indexB]; // copy element to tempArr
indexB++; // increment indexB
}
// increment indexC
indexC++;
}
while (indexA < midpt) {// 复制前子表尾部
tempArr[indexC] = arr[indexA]; // copy element to tempArr
indexA++;
indexC++;
}
while (indexB < last) {// 复制后子表尾部
tempArr[indexC] = arr[indexB]; // copy element to tempArr
indexB++;
indexC++;
}
for (int i = first; i < last; i++)// 从temp复制到array
arr[i] = tempArr[i];
}
}
2.2测试用例
public void msort() {
Integer[] intArr = { 25, 10, 7, 19, 3, 48, 12, 17, 56, 30, 21 };
Integer[] tempArr = intArr.clone();
GenericUtil.msort(intArr, tempArr, 0, intArr.length);
ArraysUtil.printArrays(intArr);
}
3.0快速排序
快速排序使用一些列递归调用算法将列表分割为若干越来越小的子列表, 这些子列表位于基准值(pivot)左右. 每个递归步骤根据作为列表中心的点值的基准进行选择.分割算法完成交换, 从而使基准值在元素排序后被放置在列表中的正确位置上.此时,下子列表只含小于或等于表准值的元素, 而上字表只含大于或等于基准值的元素.

scanUp继续向上搜索,在索引3处,scanDown停止在索引8处

继续上面的步骤,到达停止条件

在scanDown<=scanUp时,分割过程终止.如果scanDown==scanUp,那么arr[scanDown]<=pivot并且arr[scanUp>=pivot

3.2快速排序
递归调用链

3.3 快速排序查找基准值
public static <T extends Comparable<? super T>> int prvotIndex(T[] arr,
int first, int last) {
int mid, scanUp, scanDown;
T pivot, temp;
if (first == last) {// 空子列
return last;
} else if (first == last - 1) {// 一个元素的子列
return first;
} else {
mid = (first + last) / 2;// 交换prvot和范围的低端和初始化指数scanUp和scandown
pivot = arr[mid];
arr[mid] = arr[first];
arr[first] = pivot;
scanUp = first + 1;
scanDown = last - 1;
for (;;) {
while (scanUp <= scanDown && arr[scanUp].compareTo(pivot) < 0) {//每个步骤开始时都会使用索引scanUp在列表中向上移动,直至该索引停止在应归入上子列表(由大于或等于基准值的元素组成)的某个元素处
scanUp++;
}
while (pivot.compareTo(arr[scanDown]) < 0) {//索引scanDown在列表中向下移动,直至该索引停止在应归入子列表(由小于或等于基准值的元素组成)的某个元素处
scanDown--;
}
if (scanUp >= scanDown) {
break;
}
temp = arr[scanUp];//如果scandown<=scanUp,那么迭代停止.否这,两个扫描在scanUp<scanDown时停止,并且每个索引都指向位于错误列表中的某个元素.通过这两个元素的交换就能够完成列表的重新排列. 扫描结束后,索引scanDown的位置将列表分割为两个子列表.pivotIndex()方法能够交换arr[first]最后哦功能的基准值与arr[scandown],并且scanDown设置为返回值
arr[scanUp] = arr[scanDown];
arr[scanDown] = temp;
scanUp++;
scanDown++;
}
arr[first] = arr[scanDown];
arr[scanDown] = pivot;
return scanDown;
}
}