1. A simple model of computation: DFAs
-- Tape:
- Stores input.
- One arbitrarily long strip, divided into cells.
- Finite alphabet of symbols.
-- Tape head:
- Points to one cell of tape.
- Reads a symbol from active cell.
- Moves one cell at a time.
-- Machine:
- After finishing reading the input, output yes or no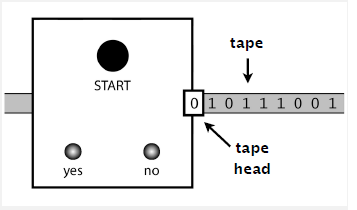
2. A universal model of computation: Turing machines
-- Tape:
- Stores input, output, and intermediate results.
- One arbitrarily long strip, divided into cells.
- Finite alphabet of symbols.
-- Tape head:
- Points to one cell of tape.
- Reads a symbol from active cell.
- Writes a symbol to active cell.
- Moves one cell at a time.
-- Machine:
- controls move back/forward, read/write
- After finishing reading the input, output yes or no
3. Church-Turing thesis:
-- Proposition. Turing machines can compute any function that can be computed by a physically harnessable process of the natural world.
-- "Thesis" and not a mathematical theorem because it's a statement about the physical world and not subject to proof.
-- Implications
- No need to seek more powerful machines or languages.
- Enables rigorous study of computation (in this universe).
-- Bottom line. Turing machine is a simple and universal model of computation.
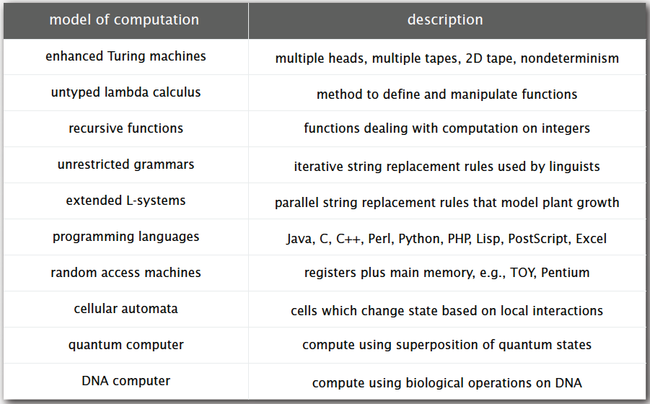
-- Many models of computation that turned out to be equivalent(Use simulation to prove models equivalent):
3. A problem is intractable if it can't be solved in polynomial time.
4. Two problems that provably require exponential time.
-- Given a constant-size program, does it halt in at most K steps? (input size = c + lg K)
-- Given N-by-N checkers board position, can the first player force a win?
5. Four fundamental problems:
-- LSOLVE: Given a system of linear equations, find a solution. Gaussian elimination solves N-by-N system in N^3 time.
-- LP: Given a system of linear inequalities, find a solution. Ellipsoid algorithm is poly-time, but was open problem for decades.

-- ILP: Given a system of linear inequalities, find a 0-1 solution. No poly-time algorithm known
-- SAT: Given a system of boolean equations, find a binary solution. No poly-time algorithm known.
6. Search problems:
-- Given an instance I of a problem, find a solution S(or reportnone exists). Must be able to efficiently(poly-time in size of instance I) check that S is a solution.
-- Factor problem is search problem: Given an n-bit integer I(input size = number of bits), find a nontrivial factor. To check solution S, long divide I by S.
7. P VS NP
-- NP: NP is the class of all search problems.
-- P: P is the class of search problems solvable in poly-time.
-- P = NP ?
8. Classifying problems:
-- Problem X poly-time reduces to problem Y if X can be solved with:
-- Polynomial number of standard computational steps.
-- Polynomial number of calls to Y.
-- If SAT poly-time reduces to Y, then we conclude that Y is (probably) intractable.
-- SAT poly-time reduces to ILP:

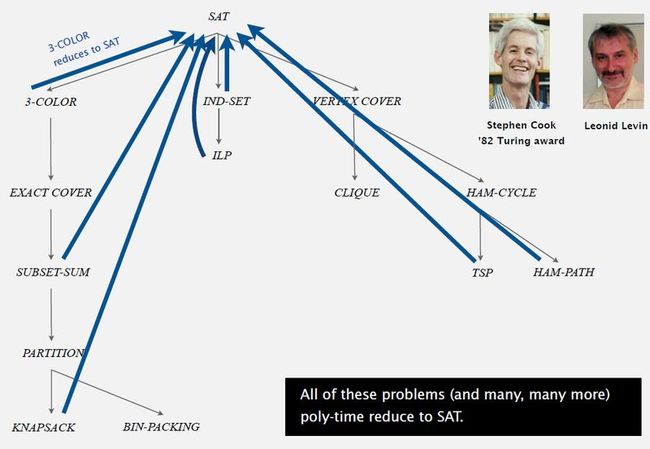
-- More poly-time reductions from SAT: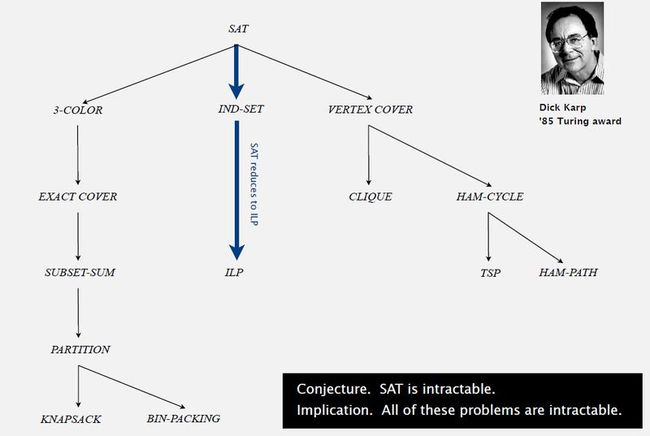
9. NP-completeness
-- An NP problem is NP-complete if every problem in NP poly-time reduce to it.
-- Cook-Levin theorem: SAT is NP-complete. (every NP problem is a SAT problem in disguise.)
-- Extremely brief proof sketch :
- Nondeterministic machine can guess the desired solution. (NFA)
- Nondeterministic: more than one possible next state.
- NP: Search problems solvable in poly time on a nondeterministic TM.
- Convert non-deterministic TM notation to SAT notation.
- If you can solve SAT, you can solve any problem in NP.
-- Corollary:
- Poly-time algorithm for SAT iff P = NP.
- No poly-time algorithm for some NP problem ⇒ none for SAT.
-- Extended Church-Turing thesis : P = search problems solvable in poly-time in the natural world.
10. Implications of Cook-Levin theorem:
11. Implications of Karp + Cook-Levin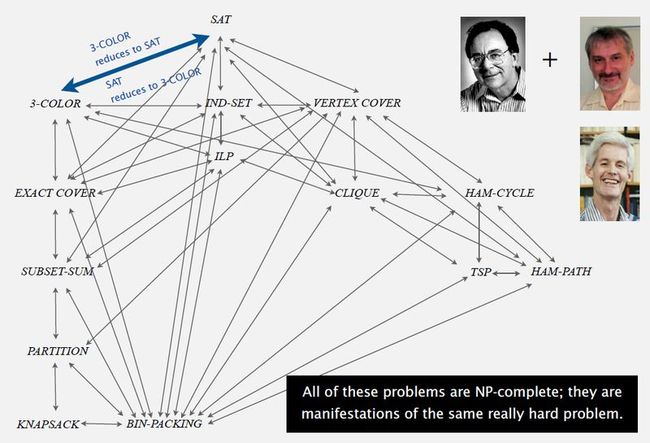
12. Use theory as a guide:
-- A poly-time algorithm for an NP-complete problem would be a stunning breakthrough (a proof that P = NP).
-- You will confront NP-complete problems in your career.
-- Safe to assume that P ≠ NP and that such problems are intractable.
-- Identify these situations and proceed accordingly.
13. Coping with intractability: Relax one of desired features.
-- Solve arbitrary instances of the problem: Special cases may be tractable.
-- Linear time algorithm for 2-SAT.(at most two variables per equation)
-- Linear time algorithm for Horn-SAT.(at most one un-negated variable per equation)
-- Solve the problem to optimality: Develop a heuristic, and hope it produces a good solution.
-- No guarantees on quality of solution.
-- TSP assignment heuristics.
-- Metropolis algorithm, simulating annealing, genetic algorithms.
-- MAX-3SAT: provably satisfy 87.5% as many clauses as possible.
-- Solve the problem in poly-time.
-- Complexity theory deals with worst case behavior.
-- Instance(s) you want to solve may be "easy."
14. Hamilton path
-- Goal: Find a simple path that visits every vertex exactly once.
-- Euler path(visit every edge exactly once) is easy, but Hamilton path is NP-complete.
-- Java Implementation:
public class HamiltonPath
{
private boolean[] marked; // vertices on current path
private int count = 0; // number of Hamiltonian paths
public HamiltonPath(Graph G)
{
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
dfs(G, v, 1);
}
//depth is the length of current path (depth of recursion)
private void dfs(Graph G, int v, int depth)
{
marked[v] = true;
if (depth == G.V()) count++;
for (int w : G.adj(v))
if (!marked[w]) dfs(G, w, depth+1); //backtrack if w is already part of path
marked[v] = false; // clean up
}
}
15. Summary
-- P. Class of search problems solvable in poly-time.
-- NP. Class of all search problems, some of which seem wickedly hard.
-- NP-complete. Hardest problems in NP.
-- Intractable. Problem with no poly-time algorithm.
16. Princeton CS Building, West Wall, Circa 2001: