Bitonic search

简介

    Bitonic search是一个和binary search比较类似的一种查找方法，不过它的过程会显得稍微复杂一点。从某种角度来说，它和我前面这篇文章里讨论过的一种binary search的一个变体很像，不过就是因为一个小小的变化，它们的解决办法就有着极大的差别。我们先来看看问题本身的描述：

    一个bitonic数组是由一个递增的整数序列后面接着一个递减的序列，假设数组里有N个唯一的数字，我们要查询给定的一个数字， 使得查找的时间尽可能的短。

3logN解决方法

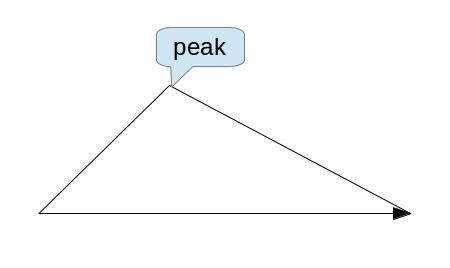
    在标出这个子标题的时候，似乎有点未卜先知的味道。我们可以先根据这个问题来分析一下。假定我们给定有这么一个数组：[1, 3, 4, 6, 9, 14, 11, 7, 5, 2, -4, -9] 。那么它们的布局应该成如下的一个形式：

    假设我们水平线的方向表示数组排列的方向，它们的数值对应这上面折线的高度，那么比如有一个点是这个数组中最大的。如果我们事先找到了这个最大的点，假设它的下标是k。那么从数组的0到k这部分是一个严格递增的序列，同样从k+1到数组末尾是一个递减的序列。如果我们熟悉binary search的话，现在应该就找到一个思路了。剩下的就是我们在这个两边的序列里分别去搜索指定的值。

    那么概括起来我们这个方法的思路如下：

    1. 找到数组最大的那个值。既然我们期望能尽可能快的找到。直接遍历搜索的时间复杂度到了O(N)。显然不太合适。不过我们也可以利用binarysearch的思路，每次对数组取中间值，如果这个值比它左边的大，表示它在左边递增的序列，如果它比左边的小，表示它在右边递减的序列。只有当它比左右两边的都大时，才能说明它就是我们找到的最大值。

    2. 找到最大值之后我们就以它为分界线，对给定的值在它两边的区域分别进行binarysearch。为什么要两边分开呢？一个是对于一个值它可能存在于左边序列，也可能存在于右边序列。另外，我们默认的binarysearch默认的是要求数组升序排列的。对于后面降序的数组我们要对这个方法做一点修改。

    下面是我们对它们各部分的实现：

public static int findPeak(int[] a) {
        int l = 0;
        int r = a.length -1;
        int mid;
        while(l <= r) {
            mid = l + (r - l) / 2;
            if(a[mid] > a[mid - 1] && a[mid] > a[mid + 1])
                return mid;
            else if(a[mid] > a[mid - 1])
                l = mid + 1;
            else if(a[mid] > a[mid + 1])
                r = mid - 1;
        }

        return -1;
    }

    这部分的实现和binarysearch很像，只是每次需要判断的时候设置一下l, r的情形不同。通过这一步findPeak之后我们就得到这个最大值所在的下标了。然后就是分别搜索实现的代码，这里分为对升序数组的搜索和降序数组的搜索：

 public static int ascBinarySearch(int[] a, int l, int r, int v) {
        if(a == null || a.length == 0)
            return -1;
        int mid;
        while(l <= r) {
            mid = l + (r - l) / 2;
            if(v > a[mid])
                l = mid + 1;
            else if(v < a[mid])
                r = mid - 1;
            else
                return mid;
        }

        return -1;
    }

 public static int desBinarySearch(int[] a, int l, int r, int v) {
        if(a == null || a.length == 0)
            return -1;
        int mid;
        while(l <= r) {
            mid = l + (r - l) / 2;
            if(v > a[mid])
                r = mid - 1;
            else if(v < a[mid])
                l = mid + 1;
            else
                return mid;
        }

        return -1;
    }

   这两个方法里第一个就是典型的binarysearch实现，第二个针对降序需要设置l, r的值的形式不一样。也就没什么其他特殊的了。

    当然，从完整实现的角度来看，我们还需要结合前面几个步骤的代码：

public static int bitonicSearch(int[] a, int v) {
        int peak = findPeak(a);
        if(peak != -1) {
            int first = ascBinarySearch(a, 0, peak, v);
            int last = desBinarySearch(a, peak + 1, a.length - 1, v);
            if(first != -1)
                return first;
            if(last != -1)
                return last;
        }
        
        return -1;
    }

    这里唯一值得注意的地方就是如果我们查找的对象找不到，在后面都统一返回负数了。从前面所有的步骤来看，第一步我们查找最大值，用的时间为logN，第二步要在两个区域里查找给定的数字，每个地方查找的时间分别为logN，所以整体的时间加起来大致上为3logN。

    这就是我们提到的一种解决方法。嗯，看起来已经相当完美了。当然，从追求完美的角度来说，我们还有没有更加快的解决方法呢？前面的方法里，我们还花了不少时间去查找这个最大的值，能不能不用查这个最大值然后也能解决呢？实际上，还有一个更猛的。

 

2logN解决方法

     我们再换一个角度来思考这个问题。前面的问题实质上是需要我们找到最大值，然后根据两边的段来查找。现在我们来看看怎么不用找最大值来解决它。针对这种布局的数列，如果我们取它们中间的元素，则这个中间的元素可能处于两种情况：

1. 中间元素处在左边递增的序列中。

2. 中间元素处在右边递减的序列中。

    我们针对这两种情况一一来分析：

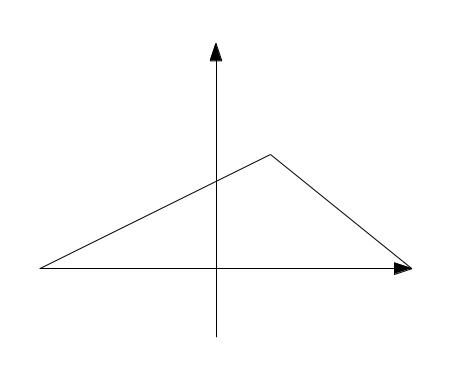
中间元素在左边递增序列

    这种情况下，对应的图如下：

    在上图中，我们假定中间的竖直的线为中间线，那么这种情况下的查找我们也需要进一步的讨论。

    当取得中间值元素，如果我们要查找的元素比我们当前的元素大，那么根据这个情况，我们知道它肯定不会在中间线分割的左边部分，它只可能在右边。这个时候它的分布很可能还是包含在右边整个的区域里的。我们如果要查找它的话，需要进一步递归的去找。

    如果我们要找的这个元素比中间元素小呢？这个时候就比较有意思了。因为它还是可能出现在左边，也可能出现在右边。这个时候，对于左边来说，我们直接使用通用的binarySearch查就可以了。对于右边的呢？因为要查的元素比目标元素小，可是右边的这个串并不是严格递减的，它中间有一部分是递增的。我们的二叉查找能奏效吗？我们再来进一步的分析一下。

    如果我们按照descending的序列情况来做查找，对于上面的序列来说，假定我们下一次再取中间值的时候，这个目标值还是小于中间值，那么，我们肯定会从中间值的右边去找，这样还是会向着递减序列的范围去趋近。假定目标值小于这次取的中间值，那么这个目标值肯定已经不在原来左边递增的序列上了，因为那个时候左边的序列值只会比目标值更大。所以说，这样子去做二叉查找还是可行的。

    概括起来的话，前面的过程可以用代码描述如下：

if(a[mid] > a[mid - 1]) {  //如果在递增序列
            if(v > a[mid]) { //目标值大于中间值，继续递归
                return bitonicSearch2(a, mid + 1, r, v);
            } else {  //目标值小于中间值，需要查找左边的递增序列和右边的递减序列
                System.out.printf("l: %d, r: %d, mid: %d", l, r, mid);
                int asc = ascBinarySearch(a, l, mid, v);
                System.out.println("asc: " + asc);
                int des = desBinarySearch(a, mid + 1, r, v);
                System.out.println("des: " + des);
                if(asc != -1)
                    return asc;
                if(des != -1)
                    return des;
                return -1;
            }
        }

     为了方便看到当前划分的情况，增加了一些输出的语句。这里的ascBinarySearch，desBinarySearch和前面的实现是一样的。

 

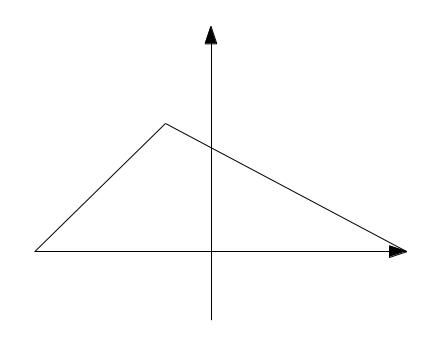
中间元素在右边递减序列

    这种情况实际上就和前面的很类似了，它对应的情况如下图：

    我们也可以得到类似的结论，当我们的目标值比中间值大的时候，我们需要对它左边的范围进行递归。否则在它的左边做递增的二叉查找，右边做递减的二叉查找。这部分的伪代码如下：

 

if(v > a[mid]) {
                return bitonicSearch2(a, l, mid, v);
            } else {
                int asc = ascBinarySearch(a, l, mid, v);
                int des = desBinarySearch(a, mid + 1, r, v);
                if(asc != -1)
                    return asc;
                if(des != -1)
                    return des;
                return -1;
            }

 

    前面贴出来的只是一个代码的片段，完整的代码如下：

public static int bitonicSearch2(int[] a, int l, int r, int v) {
        if(l > r)
            return -1;
        int mid = l + (r - l) / 2;
        if(a[mid] == v)
            return mid;
        if(a[mid] > a[mid - 1]) {
            if(v > a[mid]) {
                return bitonicSearch2(a, mid + 1, r, v);
            } else {
                System.out.printf("l: %d, r: %d, mid: %d", l, r, mid);
                int asc = ascBinarySearch(a, l, mid, v);
                System.out.println("asc: " + asc);
                int des = desBinarySearch(a, mid + 1, r, v);
                System.out.println("des: " + des);
                if(asc != -1)
                    return asc;
                if(des != -1)
                    return des;
                return -1;
            }
        } else {
            if(v > a[mid]) {
                return bitonicSearch2(a, l, mid, v);
            } else {
                int asc = ascBinarySearch(a, l, mid, v);
                int des = desBinarySearch(a, mid + 1, r, v);
                if(asc != -1)
                    return asc;
                if(des != -1)
                    return des;
                return -1;
            }
        }
    }

    我们来看看整体的代码时间复杂度，每次执行一次要么就直接递归到原来的一半，要么就规约到两个部分的binarySearch。所以它的时间复杂度只有2logN。

 

总结

    就是简简单单的一个binarySearch，通过它针对不同数组特性的变化可以牵涉出很多的变种。针对数组的递增递减特性来灵活的选择binarySearch实现，同时结合递归的方法，在很多时候还是一种有效的方式。在这里，尤其重要的是要针对不同的场景进行分析，只要把这些理解透了，后面的代码也就比较自然的出来了。

 

参考材料

http://stackoverflow.com/questions/19372930/given-a-bitonic-array-and-element-x-in-the-array-find-the-index-of-x-in-2logn

http://www.amazon.com/gp/product/032157351X/ref=s9_simh_gw_p14_d2_i2?pf_rd_m=ATVPDKIKX0DER&pf_rd_s=center-7&pf_rd_r=1WEQHVV0DA1TWXGSEKSH&pf_rd_t=101&pf_rd_p=1688200482&pf_rd_i=507846