今天继续说自然演算规则。
不过说之前先说一点题外话:每个人都有自己喜欢的东西,虽然大家都是搞开发的,不过最喜欢的也很可能不一样。你是牛人我也是牛人,只不过我们牛逼的地方不一样,我们都没有必要为了超过对方而去努力学习自己不稀罕的东西。 ——————谨以此开题吧。
上一篇数理逻辑之 自然演算规则(一) 说道了合取规则,应该还蛮简单的吧。
看第二个规则:(Ⅱ)双重否定规则
直觉上,一个公式与它的双重否定 所表达的内容是一样的。例如,
It is not true that it does not rain. 和It rains. 是一回事。
知道“It rains.”, 如果愿意,我们可以用更复杂的方式来陈述这一事实。“ It is not true that it does not rain. ” 因此我们得到下面的双重否定引入与消去规则:
![]()
既然我们都能看懂合取规则,这个也可以吧:两条规则,第一条是引入规则,第二条是消去规则。
我们来看一个例子:例5 证明相继式 p, ﹁﹁(q∧r) |— ﹁﹁p∧r是有效的
1 p 前提假设 2 ﹁﹁(q∧r) 前提假设 3 ﹁﹁p ﹁﹁i 1 4 q∧r ﹁﹁e 2 5 r ∧e2 4 6 ﹁﹁p∧r ∧i 3,5
前两行是前提,第三行对第一行使用了双重否定引入规则,第四行对第二行使用了双重否定消去规则,第五航对第四行使用了前面学过的合取规则,第六行根据合取规则得到了结论。证明完毕!
嗨列位看官,能不能别喊“太简单了吧”。规则就是这么简单,但是你要把每一条都秒懂才是难的。
下条是(Ⅲ) 蕴含消去规则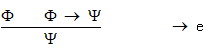
这个也比较简单,通过两个前提得到一个显而易见的结论。比如
p: It rained. p→q: If it rained, then the street is wet. q: The street is wet.
如果我们知道天下雨,而且我们知道天下雨街道就会湿。那么我们综合这两则信息就能得出“街道确实湿了”的结论。这说明,根据我们通常的直觉,蕴含消去规则的合理性是显而易见的。
我们再看另一个例子(来自于程序设计)
p: The value of the program’s input is an integer. p→q: If the program’s input is an integer, then the program output a boolean.
在这个例子中,如果程序输入是一个整数,我们可以断定程序输出是一个布尔值。
要强调的是:p的出现是绝对必要的。如果输入不是整数,即使程序满足p→q, 我们无法得到q。
例6 证明相继式 p, p→q, p →(q → r) |— r是有效的
1 p 前提假设 2 p→q 前提假设 3 p →(q → r) 前提假设 4 q→r →e 1,3 5 q →e 1,2 6 r →e 5,4
这个太简单了我都不想解释了,不过呀强调的一点是第六行是对第五行和第四行使用了蕴含消去规则,而不能写成→e 4,5。规则就是规则,我们很机械。
我去,咋这么大只啊?不好意思,图片没处理好。
这个规则会让你想起曾经反复使用的逆否命题。不过千万不要和别人说MT规则就是逆否命题和原命题等价的意思,因为写法完全不同。
例7 证明相继式 p→(q→r), p, ﹁r |— ﹁q 是有效的
1 p→(q→r) 前提假设 2 p 前提假设 3 ﹁r 前提假设 4 q→r →e 2,1 5 ﹁q MT 4,3
我们在第五行根据第四行和第三行得出来了结论,好简单!
例8 证明相继式 ﹁ p→q, ﹁q |— p 是有效的.
1 ﹁ p→q 前提假设 2 ﹁q 前提假设 3 ﹁﹁p MT 1,2 4 p ﹁﹁e 3
第三行得到一个诡异的结论,第四行使用双重否定消去等到了证明。
谨记,我们不能从前两行直接得出第四行,因为没有这样的规则。
不知道走到这里感觉怎么样。如果你依然头脑完全清新,说明你是一枚牛人。
不过后面来的规则可能会让你措手不及。
既然这样,我们先歇一下,做两个小题:
思考题: 证明下列相继式 是有效的. ① ﹁ p→q, ﹁ q |— p ② p → ﹁q , q |— ﹁ p
记住千万不要无中生有,使用自己创造的规则。题目越简单,往往会出现很多自编自导的规则。
