算法小练习--歌德巴赫猜想
晚上没事,尝试解决一个小的算法问题。 我的算法比较弱,也没查什么参考资料,自己想的思路。肯定有更好的解法。
1. 歌德巴赫猜想
所有大于等于6的偶数都可以表示成两个(奇)素数之和。给定1-10000;要求找出每一个可以表示为两素数之和的数,如果有多对,则只需要输出其中之一即可。
输出:
N = a + b;
N=1-10000;对于不能表示的就不用输出。
a,b为两个素数。
要求:复杂度较低,代码可运行。
2. 思路:
1. 找到1-10000范围内的素数, 得到一个有序数组A (时间复杂度为O(nlogn))
2. 对1-10000范围内的数进行遍历. 对每个数 i, 使用二分查找确定它在有序数组A中的"位置" pos (若存在,则为数组下标;若不存在,则为这个数插入该数组后仍能保证数组的大致位置) (时间复杂度为O(nlogn))
3. 从有序数组A的pos位置开始,令num = A[pos],二分查找确定 i - num是否也在这个数组A中。 若在, 则表示i可以用两个素数之和表示。否则, pos递减继续查找 (时间复杂度 O(n * n * logn) ??? )
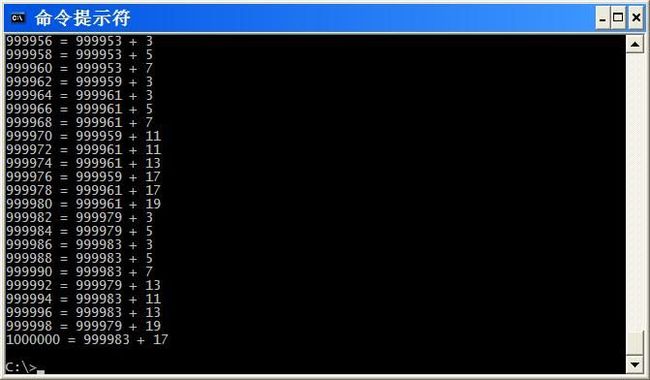
第1步生成素数列表应该有更好的方法。 第3步感觉比较低效, 但实际运行时发现pos需要递减的情况比较少。也就是说,一个很大的偶数,基本上都会被分解成一个很大的素数和一个非常小的素数。下面是运行结果。
3. 代码
# encoding: utf-8
import math
from timeit import Timer
from functools import partial
# 生成素数列表
# 版本一. 比较低效
def sushu(n):
num = 2
alist = [2]
for i in range(3, n + 1):
istrue = True
#for j in range(2, int(math.sqrt(i))):
for j in range(2, i / 2 + 1):
if i % j == 0:
istrue = False
break
if istrue:
alist.append(i)
return alist
# 生成素数列表
# 版本二
def sushu2(n):
num = 2
alist = [2]
for i in range(3, n + 1):
istrue = True
for j in range(2, int(math.sqrt(i)) + 1):
#for j in range(2, i / 2):
if i % j == 0:
istrue = False
break
if istrue:
alist.append(i)
return alist
# 生成素数列表
# 版本三
def sushu3(n):
#num = 2
alist = []
for i in range(3, n + 1, 2):
istrue = True
for j in range(3, int(math.sqrt(i)) + 1):
#for j in range(2, i / 2):
if i % j == 0:
istrue = False
break
if istrue:
alist.append(i)
return alist
# 通过二分查找找到alist中最接近 n的数的位置
def bin_search(alist, n):
low = 0
high = len(alist)
while low < high:
mid = low + (high - low) / 2
if n == alist[mid]:
return mid
elif n < alist[mid]:
high = mid - 1
else:
low = mid + 1
return low
# 所有大于等于6的偶数都可以表示成两个(奇)素数之和。
def split(n):
# 素数列表
alist = sushu3(n)
alist_len = len(alist)
for i in range(8, n + 1, 2):
pos = bin_search(alist, i)
#print pos
# 修正pos
if pos >= alist_len:
pos = alist_len - 1
isok = 0
while pos > 0:
isok = 1
#print pos >= alist_len
j = i - alist[pos]
# TODO in 是否低效
if j in alist:
isok = 2
break
pos -= 1
'''
if isok == 2:
print '%d = %d + %d' %(i, alist[pos], i - alist[pos])
elif isok == 1:
print '%d = 不能表示' % (i)
else:
print '%d = 运行异常' % (i)
'''
# 所有大于等于6的偶数都可以表示成两个(奇)素数之和。
def split2(n):
# 素数列表
alist = sushu3(n)
alist_len = len(alist)
for i in range(8, n + 1, 2):
pos = bin_search(alist, i)
#print pos
# 修正pos
if pos >= alist_len:
pos = alist_len - 1
isok = 0
while pos > 0:
isok = 1
#print pos >= alist_len
j = i - alist[pos]
if j == alist[bin_search(alist, j)]:
isok = 2
break
pos -= 1
'''
if isok == 2:
print '%d = %d + %d' %(i, alist[pos], i - alist[pos])
elif isok == 1:
print '%d = 不能表示' % (i)
else:
print '%d = 运行异常' % (i)
'''
if __name__ == '__main__':
#print sushu(100)
if False:
t = Timer(partial(sushu, 10000))
print t.timeit(10)
t2 = Timer(partial(sushu2, 10000))
print t2.timeit(10)
t3 = Timer(partial(sushu3, 10000))
print t3.timeit(10)
if False:
print sushu(100)
print sushu2(100)
print sushu3(100)
if False:
alist = sushu3(100)
print alist
for x in [96, 100, 110]:
pos = bin_search(alist, x)
print 'pos = ', pos
#print alist[pos - 1], alist[pos], alist[pos + 1]
if True:
t = Timer(partial(split, 10000))
print t.timeit(10)
t2 = Timer(partial(split2, 10000))
print t2.timeit(10)