【算法复习二】传统基本算法(分治----残缺棋盘问题)
• 问题描述:
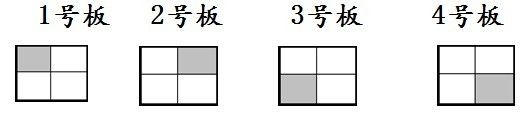
残缺棋盘是一个有2k×2k(k≥1)个方格的棋盘,其中恰有一个方格残缺。如图给出k=1时各种可能的残缺棋盘,其中残缺的方格用阴影表示。
• 残缺棋盘问题就是要用这四种三格板覆盖更大的残缺棋盘。在此覆盖中要求:
1)两个三格板不能重叠
2)三格板不能覆盖残缺方格,但必须覆盖其他所有的方格。
小格子数(2k×2k -1)三格板中小格子数3。所以所需要的三格板总数为(2k×2k -1 )/3。
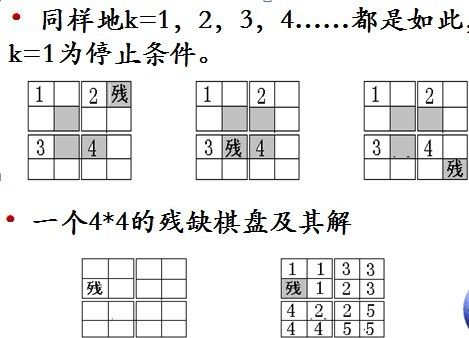
• 例如,一个4*4的残缺棋盘2k*2k
以k=2时的问题为例,用二分法进行分解,得到的四个k=1的棋盘。但要注意这四个棋盘,并不都是与原问题相似且独立的子问题。
因为当如图中的残缺方格在左上部时,第1个子问题与原问题相似,而右上角、左下角和右下角三个子棋盘(也就是图中标识为2、3、4号子棋盘),并不是原问题的相似子问题,自然也就不能独立求解了。当使用一个①号三格板覆盖2、3、4号三个子棋盘的各一个方格后,我们把覆盖后的方格,也看作是残缺方格(称为“伪”残缺方格),这时的2、3、4号子问题就是独立且与原问题相似的子问题了。
• 问题分析
从以上例子还可以发现
当残缺方格在第1个子棋盘,用①号三格板覆盖其余三个子棋盘的交界方格,可以使另外三个子棋盘转化为独立子问题;
当残缺方格在第2个子棋盘时,则首先用②号三格板进行棋盘覆盖
当残缺方格在第3个子棋盘时,则首先用③号三格板进行棋盘覆盖
当残缺方格在第4个子棋盘时,则首先用④号三格板进行棋盘覆盖,这样就使另外三个子棋盘转化为独立子问题。
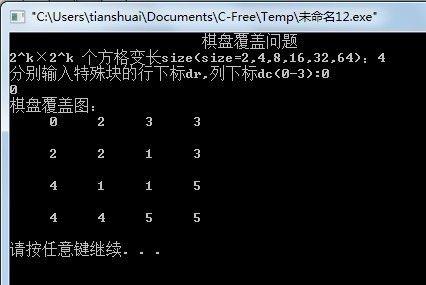
程序代码思路:
表示方法:每个三格板需要用同一个数字表示,不同三格板编号不同。
源码:
分治递归执行步骤:
1)chessBoard(0, 0, 0, 0, 4);
{ t=1; s=2;
chessBoard(0, 0, 0, 0, 2);
{ t=2; s=1;
chessBoard(0, 0, 0, 0, 1);
{ s==1
return
}
以下三步
将左上角 三格板 用t=2覆盖
}
return
以下三步 对右上递归 先 用t=1 覆盖左下
左下递归 先 用t=1 覆盖右上
右下递归 先 用t=1 覆盖左上
递归处理类似。
}