缓存淘汰算法系列之1——LRU类
1. LRU
1.1. 原理
LRU(Least recently used,最近最少使用)算法根据数据的历史访问记录来进行淘汰数据,其核心思想是“如果数据最近被访问过,那么将来被访问的几率也更高”。
1.2. 实现
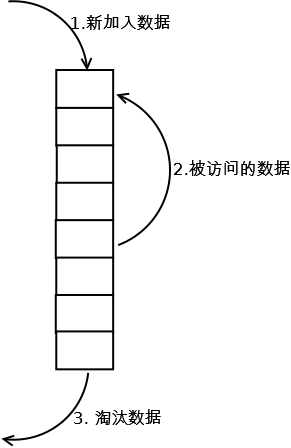
最常见的实现是使用一个链表保存缓存数据,详细算法实现如下:
1. 新数据插入到链表头部;
2. 每当缓存命中(即缓存数据被访问),则将数据移到链表头部;
3. 当链表满的时候,将链表尾部的数据丢弃。
1.3. 分析
【命中率】
当存在热点数据时,LRU的效率很好,但偶发性的、周期性的批量操作会导致LRU命中率急剧下降,缓存污染情况比较严重。
【复杂度】
实现简单。
【代价】
命中时需要遍历链表,找到命中的数据块索引,然后需要将数据移到头部。
2. LRU-K(描述有误,请勿参考)
2.1. 原理
LRU-K中的K代表最近使用的次数,因此LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题,其核心思想是将“最近使用过1次”的判断标准扩展为“最近使用过K次”。
2.2. 实现
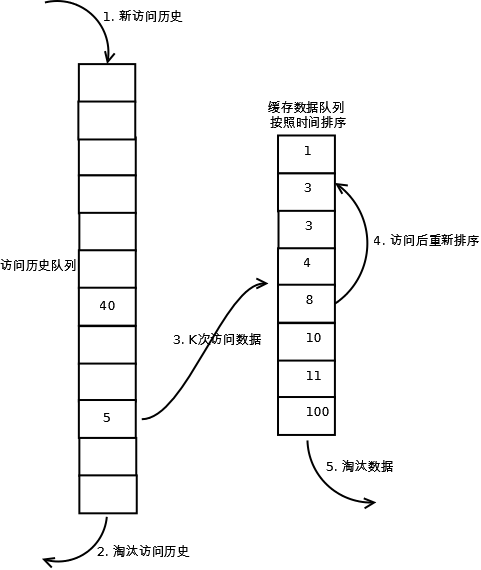
相比LRU,LRU-K需要多维护一个队列,用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候,才将数据放入缓存。当需要淘汰数据时,LRU-K会淘汰第K次访问时间距当前时间最大的数据。详细实现如下:
1. 数据第一次被访问,加入到访问历史列表;
2. 如果数据在访问历史列表里后没有达到K次访问,则按照一定规则(FIFO,LRU)淘汰;
3. 当访问历史队列中的数据访问次数达到K次后,将数据索引从历史队列删除,将数据移到缓存队列中,并缓存此数据,缓存队列重新按照时间排序;
4. 缓存数据队列中被再次访问后,重新排序;
5. 需要淘汰数据时,淘汰缓存队列中排在末尾的数据,即:淘汰“倒数第K次访问离现在最久”的数据。
LRU-K具有LRU的优点,同时能够避免LRU的缺点,实际应用中LRU-2是综合各种因素后最优的选择,LRU-3或者更大的K值命中率会高,但适应性差,需要大量的数据访问才能将历史访问记录清除掉。
2.3. 分析
【命中率】
LRU-K降低了“缓存污染”带来的问题,命中率比LRU要高。
【复杂度】
LRU-K队列是一个优先级队列,算法复杂度和代价比较高。
【代价】
由于LRU-K还需要记录那些被访问过、但还没有放入缓存的对象,因此内存消耗会比LRU要多;当数据量很大的时候,内存消耗会比较可观。
LRU-K需要基于时间进行排序(可以需要淘汰时再排序,也可以即时排序),CPU消耗比LRU要高。
3. Two queues(2Q)
3.1. 原理
Two queues(以下使用2Q代替)算法类似于LRU-2,不同点在于2Q将LRU-2算法中的访问历史队列(注意这不是缓存数据的)改为一个FIFO缓存队列,即:2Q算法有两个缓存队列,一个是FIFO队列,一个是LRU队列。
3.2. 实现
当数据第一次访问时,2Q算法将数据缓存在FIFO队列里面,当数据第二次被访问时,则将数据从FIFO队列移到LRU队列里面,两个队列各自按照自己的方法淘汰数据。详细实现如下:
1. 新访问的数据插入到FIFO队列;
2. 如果数据在FIFO队列中一直没有被再次访问,则最终按照FIFO规则淘汰;
3. 如果数据在FIFO队列中被再次访问,则将数据移到LRU队列头部;
4. 如果数据在LRU队列再次被访问,则将数据移到LRU队列头部;
5. LRU队列淘汰末尾的数据。
注:上图中FIFO队列比LRU队列短,但并不代表这是算法要求,实际应用中两者比例没有硬性规定。
3.3. 分析
【命中率】
2Q算法的命中率要高于LRU。
【复杂度】
需要两个队列,但两个队列本身都比较简单。
【代价】
FIFO和LRU的代价之和。
2Q算法和LRU-2算法命中率类似,内存消耗也比较接近,但对于最后缓存的数据来说,2Q会减少一次从原始存储读取数据或者计算数据的操作。
4. Multi Queue(MQ)
4.1. 原理
MQ算法根据访问频率将数据划分为多个队列,不同的队列具有不同的访问优先级,其核心思想是:优先缓存访问次数多的数据。
4.2. 实现
MQ算法将缓存划分为多个LRU队列,每个队列对应不同的访问优先级。访问优先级是根据访问次数计算出来的,例如
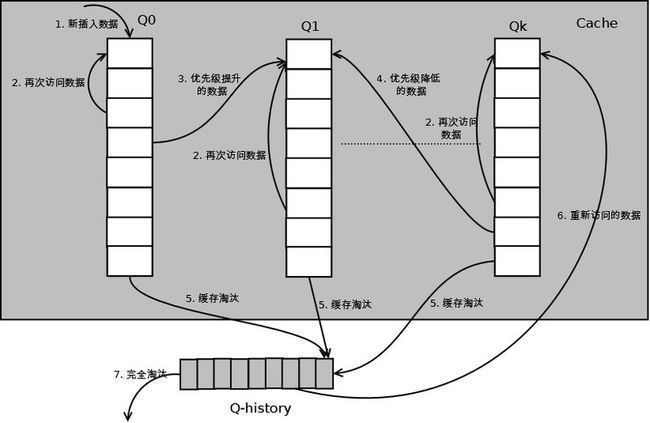
详细的算法结构图如下,Q0,Q1....Qk代表不同的优先级队列,Q-history代表从缓存中淘汰数据,但记录了数据的索引和引用次数的队列:
如上图,算法详细描述如下:
1. 新插入的数据放入Q0;
2. 每个队列按照LRU管理数据;
3. 当数据的访问次数达到一定次数,需要提升优先级时,将数据从当前队列删除,加入到高一级队列的头部;
4. 为了防止高优先级数据永远不被淘汰,当数据在指定的时间里访问没有被访问时,需要降低优先级,将数据从当前队列删除,加入到低一级的队列头部;
5. 需要淘汰数据时,从最低一级队列开始按照LRU淘汰;每个队列淘汰数据时,将数据从缓存中删除,将数据索引加入Q-history头部;
6. 如果数据在Q-history中被重新访问,则重新计算其优先级,移到目标队列的头部;
7. Q-history按照LRU淘汰数据的索引。
4.3. 分析
【命中率】
MQ降低了“缓存污染”带来的问题,命中率比LRU要高。
【复杂度】
MQ需要维护多个队列,且需要维护每个数据的访问时间,复杂度比LRU高。
【代价】
MQ需要记录每个数据的访问时间,需要定时扫描所有队列,代价比LRU要高。
注:虽然MQ的队列看起来数量比较多,但由于所有队列之和受限于缓存容量的大小,因此这里多个队列长度之和和一个LRU队列是一样的,因此队列扫描性能也相近。
5. LRU类算法对比
由于不同的访问模型导致命中率变化较大,此处对比仅基于理论定性分析,不做定量分析。
| 对比点 |
对比 |
| 命中率 |
LRU-2 > MQ(2) > 2Q > LRU |
| 复杂度 |
LRU-2 > MQ(2) > 2Q > LRU |
| 代价 |
LRU-2 > MQ(2) > 2Q > LRU |
实际应用中需要根据业务的需求和对数据的访问情况进行选择,并不是命中率越高越好。例如:虽然LRU看起来命中率会低一些,且存在”缓存污染“的问题,但由于其简单和代价小,实际应用中反而应用更多。
1. LFU类
1.1. LFU
1.1.1. 原理
LFU(Least Frequently Used)算法根据数据的历史访问频率来淘汰数据,其核心思想是“如果数据过去被访问多次,那么将来被访问的频率也更高”。
1.1.2. 实现
LFU的每个数据块都有一个引用计数,所有数据块按照引用计数排序,具有相同引用计数的数据块则按照时间排序。
1. 新加入数据插入到队列尾部(因为引用计数为1);
2. 队列中的数据被访问后,引用计数增加,队列重新排序;
3. 当需要淘汰数据时,将已经排序的列表最后的数据块删除。
1.1.3. 分析
l 命中率
一般情况下,LFU效率要优于LRU,且能够避免周期性或者偶发性的操作导致缓存命中率下降的问题。但LFU需要记录数据的历史访问记录,一旦数据访问模式改变,LFU需要更长时间来适用新的访问模式,即:LFU存在历史数据影响将来数据的“缓存污染”效用。
l 复杂度
需要维护一个队列记录所有数据的访问记录,每个数据都需要维护引用计数。
l 代价
需要记录所有数据的访问记录,内存消耗较高;需要基于引用计数排序,性能消耗较高。
1.2. LFU*
1.2.1. 原理
基于LFU的改进算法,其核心思想是“只淘汰访问过一次的数据”。
1.2.2. 实现
LFU*数据缓存实现和LFU一样,不同的地方在于淘汰数据时,LFU*只淘汰引用计数为1的数据,且如果所有引用计数为1的数据大小之和都没有新加入的数据那么大,则不淘汰数据,新的数据也不缓存。
1.2.3. 分析
l 命中率
和LFU类似,但由于其不淘汰引用计数大于1的数据,则一旦访问模式改变,LFU*无法缓存新的数据,因此这个算法的应用场景比较有限。
l 复杂度
需要维护一个队列,记录引用计数为1的数据。
l 代价
相比LFU要低很多,不需要维护所有数据的历史访问记录,只需要维护引用次数为1的数据,也不需要排序。
1.3. LFU-Aging
1.3.1. 原理
基于LFU的改进算法,其核心思想是“除了访问次数外,还要考虑访问时间”。这样做的主要原因是解决LFU缓存污染的问题。
1.3.2. 实现
虽然LFU-Aging考虑时间因素,但其算法并不直接记录数据的访问时间,而是通过平均引用计数来标识时间。
LFU-Aging在LFU的基础上,增加了一个最大平均引用计数。当当前缓存中的数据“引用计数平均值”达到或者超过“最大平均引用计数”时,则将所有数据的引用计数都减少。减少的方法有多种,可以直接减为原来的一半,也可以减去固定的值等。
1.3.3. 分析
l 命中率
LFU-Aging的效率和LFU类似,当访问模式改变时,LFU-Aging能够更快的适用新的数据访问模式,效率要高。
l 复杂度
在LFU的基础上增加平均引用次数判断和处理。
l 代价
和LFU类似,当平均引用次数超过指定阈值(Aging)后,需要遍历访问列表。
1.4. LFU*-Aging
1.4.1. 原理
LFU*和LFU-Aging的合成体。
1.4.2. 实现
略。
1.4.3. 分析
l 命中率
和LFU-Aging类似。
l 复杂度
比LFU-Aging简单一些,不需要基于引用计数排序。
l 代价
比LFU-Aging少一些,不需要基于引用计数排序。
1.5. Window-LFU
1.5.1. 原理
Windows-LFU是LFU的一个改进版,差别在于Window-LFU并不记录所有数据的访问历史,而只是记录过去一段时间内的访问历史,这就是Window的由来,基于这个原因,传统的LFU又被称为“Perfect-LFU”。
1.5.2. 实现
与LFU的实现基本相同,差别在于不需要记录所有数据的历史访问数据,而只记录过去一段时间内的访问历史。具体实现如下:
1)记录了过去W个访问记录;
2)需要淘汰时,将W个访问记录按照LFU规则排序淘汰
举例如下:
假设历史访问记录长度设为9,缓存大小为3,图中不同颜色代表针对不同数据块的访问,同一颜色代表针对同一数据的多次访问。
样例1:黄色访问3次,蓝色和橘色都是两次,橘色更新,因此缓存黄色、橘色、蓝色三个数据块
样例2:绿色访问3次,蓝色两次,暗红两次,蓝色更新,因此缓存绿色、蓝色、暗红三个数据块
1.5.3. 分析
l 命中率
Window-LFU的命中率和LFU类似,但Window-LFU会根据数据的访问模式而变化,能够更快的适应新的数据访问模式,”缓存污染“问题不严重。
l 复杂度
需要维护一个队列,记录数据的访问流历史;需要排序。
l 代价
Window-LFU只记录一部分的访问历史记录,不需要记录所有的数据访问历史,因此内存消耗和排序消耗都比LFU要低。
1.6. LFU类算法对比
由于不同的访问模型导致命中率变化较大,此处对比仅基于理论定性分析,不做定量分析。
| 对比点 |
对比 |
| 命中率 |
Window-LFU/LFU-Aging > LFU*-Aging > LFU > LFU* |
| 复杂度 |
LFU-Aging > LFU> LFU*-Aging >Window-LFU > LFU* |
| 代价 |
LFU-Aging > LFU > Window-LFU > LFU*-Aging > LFU*
|
缓存淘汰算法系列之3——FIFO类
1 FIFO
1.1. 原理
按照“先进先出(First In,First Out)”的原理淘汰数据。
1.2. 实现
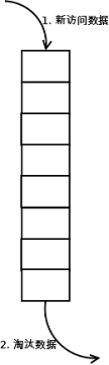
1. 新访问的数据插入FIFO队列尾部,数据在FIFO队列中顺序移动;
2. 淘汰FIFO队列头部的数据;
1.3. 分析
l 命中率
命中率很低,因为命中率太低,实际应用中基本上不会采用。
l 复杂度
简单
l 代价
实现代价很小。
2. Second Chance
2.1. 原理
FIFO算法的改进版,其思想是“如果被淘汰的数据之前被访问过,则给其第二次机会(Second Chance)”。
2.2. 实现
每个数据会增加一个访问标志位,用于标识此数据放入缓存队列后是否被再次访问过。
如上图,A是FIFO队列中最旧的数据,且其放入队列后没有被再次访问,则A被立刻淘汰;否则如果放入队列后被访问过,则将A移到FIFO队列头,并且将访问标志位清除。
如果所有的数据都被访问过,则经过一次循环后就会按照FIFO的原则淘汰数据。
2.3. 分析
l 命中率
命中率比FIFO高。
l 复杂度
与FIFO相比,需要记录数据的访问标志位,且需要将数据移动。
l 代价
实现代价比FIFO高。
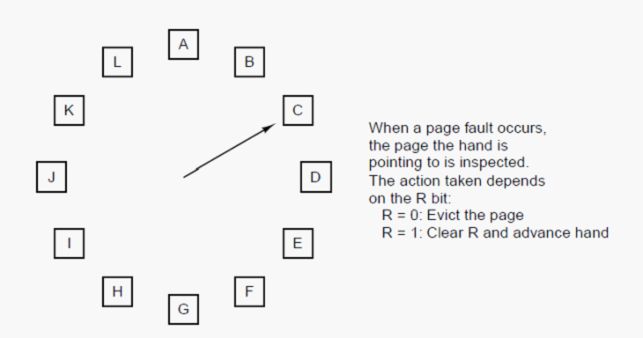
3. Clock
3.1. 原理
Clock是Second Chance的改进版,通过一个环形队列,避免将数据在FIFO队列中移动。
3.2. 实现
l 当前指针指向C,如果C被访问过,则清除C的访问标志,并将指针指向D;
l 如果C没有被访问过,则将新数据插入到C的位置,将指针指向D。
3.3. 分析
l 命中率
命中率比FIFO高,和Second Chance一样。
l 复杂度
与FIFO相比,需要记录数据的访问标志位,且需要将数据指针移动。
l 代价
实现代价比FIFO高,比Second Chance低。
4. FIFO类算法对比
| 对比点 |
对比 |
| 命中率 |
Clock = Second Chance > FIFO |
| 复杂度 |
Second Chance > Clock > FIFO |
| 代价 |
Second Chance > Clock > FIFO |
由于FIFO类算法命中率相比其他算法要低不少,因此实际应用中很少使用此类算法。