内螺旋矩阵算法分析
算法说明:
在屏幕上打印如下结果:
int i=5;
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
int i=6
1 2 3 4 5 6
20 21 22 23 24 7
19 32 33 34 25 8
18 31 36 35 26 9
17 30 29 28 27 10
16 15 14 13 12 11
算法代码:
public class HelixAlgo {
public void print(int len){
if(len<=0){
System.out.println("请输入大于0的整数!");
return;
}
int[][] helix=calculate(len);
for(int i=0;i<helix.length;i++){
for(int j=0;j<helix[i].length;j++){
System.out.print(helix[i][j]+"\t");
}
System.out.println("");
}
}
private int[][] calculate(int len){
int[][] helix=new int[len][len];
int min=0,max=len-1;//行列的最大最小值
int row=0,col=0;
for(int i=0;i<len*len;i++){
helix[row][col]=i+1;
if(row==min&&col<max){
col++;
}else if(row<max&&col==max){
row++;
}else if(row==max&&col>min){
col--;
}else if(row>min&&col==min){
row--;
}
if(row-1==min&&col==min){ //在一个周期结束时修改最大最小值
min++;
max--;
}
}
return helix;
}
public static void main(String[] args){
HelixAlgo algo=new HelixAlgo();
algo.print(6);
}
}
算法分析:
这是一道方阵题,根据结果矩阵的变化规律,此处不妨将其叫做"内螺旋矩阵"。
先画出该方阵的索引图(以6阶方阵为例):
00 01 02 03 04 05 //第一位为行索引,第二位为列索引
10 11 12 13 14 15
20 21 22 23 24 25
30 31 32 33 34 35
40 41 42 43 44 45
50 51 52 53 54 55
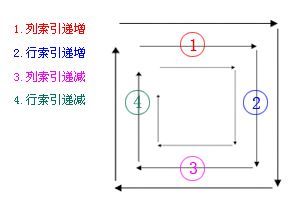
根据题目给出的结果方阵,可画出值递增变化的流向图:
根据上面的流向图,可按流向的方向将变化过程分成4中状态:
1.列索引递增
条件:行索引为最小值,列索引未达到最大值
结果:行索引为最小值,列索引达到最大值
2.行索引递增
条件:列索引为最大值,行索引未达到最大值
结果:列索引为最大值,行索引达到最大值
3.列索引递减
条件:行索引为最大值,列索引未达到最小值
结果:行索引为最大值,列索引达到最小值
4.行索引递减
条件:列索引为最小值,行索引未达到最小值
结果:列索引为最小值,行索引达到最小值
这是一个典型的状态机:当状态的行为使状态达到其结果后,将自动满足另一个状态,即状态是自动流转的。因此在代码实现中并不需要关注状态何时结束(即状态的结果),我们需要做的只是确认在合适的条件下进入合适的状态。
四种状态分别对应四个条件,因此在代码实现中可使用一个4分支的条件语句,由上面对各状态的条件描述不难写出这个条件语句(条件式中的变量row、col、rmin、rmax、cmin、cmax分别对应当前行索引、当前列索引、行索引最小值、行索引最大值、列索引最小值、列索引最大值,下文中也将使用这几个变量代表这些值,不再赘述):
if(row==rmin&&col<cmax){ //列索引递增
...
}else if(row<rmax&&col==cmax){ //行索引递增
...
}else if(row==rmax&&col>cmin){ //列索引递减
...
}else if(row>rmin&&col==cmin){ //行索引递减
...
}
有了流转条件,下面我们来分析边界条件
仔细分析不难发现,该题存在两种边界条件:状态机运行的边界条件和状态机流转的边界条件
状态机运行的边界条件,即状态机启动和停止的条件
其中启动条件很容易确定,结果集的递增是从方阵的[00]位置开始,因此只需将行列索引的初始位置调整至[00]处即可:
int row=0; int col=0;
对于不同阶数的方阵(特别是偶数阶方阵),内螺旋矩阵的结束位置并不固定,故由结束位置来作为状态机停止的条件并不合适。分析下结果方阵可看出:无论其变化规则如何,都是要填满方阵上的各个位。换句话说:只要方阵上的各个位都被填满了,这个状态机也就完成使命了。对于n阶方阵共有n*n个索引位,因此只要完成了n*n次填位操作,即可停止状态机的运行,代码片段如下(对于矩阵题,一般使用二维数组来存储各个索引位的值):
int[][] helix=new int[n][n];
for(int i=0;i<n*n;i++){
...
helix[row][col]=索引位对应的值;
...
}
状态机流转的边界条件,即状态发生改变的条件,从上述的状态结果中很容易看出四个状态对应的流转边界:列索引最大值、行索引最大值、列索引最小值、行索引最小值。对于内螺旋矩阵这四个值是在不断变化的,简单分析下就能看出其变化规律:
列索引递增结束后行索引最小值增一
行索引递增结束后列索引最大值减一
列索引递减结束后行索引最大值减一
行索引递减结束后列索引最小值增一
转换成代码,即:
if(row==rmin&&col==cmax){ //列索引递增边界
rmin++;
}else if(row==rmax&&col==cmax){ //行索引递增边界
cmax--;
}else if(row==rmax&&col==cmin){ //列索引递减边界
rmax--;
}else if(row==rmin&&col==cmin){ //行索引递减边界
cmin++;
}
深入分析下这个变化规律可发现该变化的周期为螺旋的一圈(注意:螺旋的一圈是不封口的!),在一个周期内,四个边界独立变化,故可在周期结束时统一修改边界变化:
if(row-1==rmin&&col==cmin){ //再次提醒,这里所谓一个周期的结束(螺旋的一圈)是不封口的!
rmin++;
cmax--;
rmax--;
cmin++;
}
周期结束后,行列索引的最大值均减一,最小值均加一,故可考虑将四个变量简化成两个变量max,min分别代表行列索引的最大值和最小值:
if(row-1==min&&col==min){
min++;
max--;
}
将以上分析中的代码片段整合便得到了该题的完整算法逻辑
矩阵题的一般解题思路类似于此,希望对大家有所帮助。