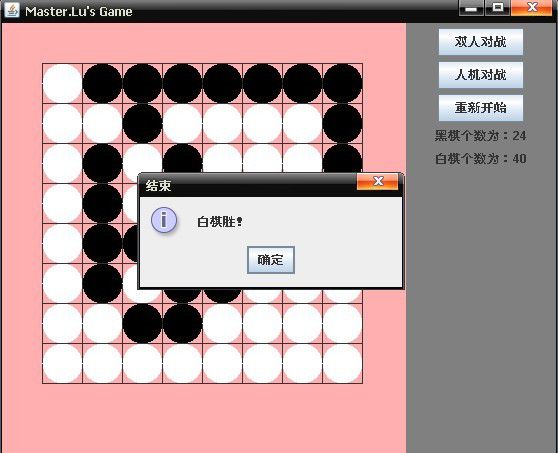
初涉黑白棋之简单双人对战

          黑白棋，又称翻转棋，还有个说法叫奥赛罗棋，具体得名我并未去考

证。下棋方式很简单，是在游戏中通过相互翻转对方的棋子，最后以棋盘

上谁的棋子多来判断胜负。
      第一次接触到黑白棋是高四复读时。那时由于学校离家较远，为了方

便和家里联系，本人得到了生平第一部移动交通工具——一部与家中座机绑

定的小灵通。而小灵通上可怜的三个游戏，也成了无聊时瞎捣鼓的东西。

这三个游戏，一是贪吃蛇，而是打地鼠，这两样由于本人的手指实在是笨

拙，硬是反应不过来而放弃。于是经常玩的，也只有剩下的那个黑白棋了

。虽然没有刻意去了解规则，可玩多了也自然上手了，稍微还掌握了一点

小小的规律，以至到后面几乎每次都能赢。（现在看来那个机器算法还是

比较烂的……）说起来，小灵通上的这个游戏，竟陪我走过了那段最难熬

的岁月。（高考的孩子伤不起啊！第一年没考上接着去复读的更伤不起啊

有木有……）或许是有这种情愫在，当龙哥让我们选择项目时，我毫不犹

豫选择了黑白棋。（完了才发现整个小组除我之外大家做的都是五子棋…

…）
      废话不多说了，现在来说黑白棋的程序。首先是布置界面，方法与五

子棋无异，在参考了书上的代码之后很快便画出了棋盘，并在棋盘中心布

好了初始的四个棋子。

 
      接下来就是下子的问题了，这时才发现，事情没有开始想象的那么简

单。黑白棋下子并不像五子棋那样，只要有空置的位置就行，而是需要判

定，只有当所在点直线方向上有可以翻转的对方棋子以及己方棋子相夹时

才能下，并且下过之后还要翻转中间所夹的异色棋子。这里便涉及到两个

方面，判断下子和改变颜色。
      先说判断一个点是否能下的问题，这里先设了一个boolean型的二维

数组，命名为ifcan，用于记录每个格子是否可下的信息。这里单独用一

个方法来写以便反复调用。当然，在给某处赋值之前一定要遍历，在这里

的话，就需要遍历该点周围横竖斜八个方向。由于遍历所得的信息之后改

变颜色还要用到，于是单独分出了一个遍历的方法counts()，代码如下：

/**对某点遍历的方法*/
	public void counts(int i,int j){
			
		/**横向遍历*/
		//东向遍历
		if(i!=gs){
			for(int k =1 ;k<gs-i+1;k++){
				if(c[i+k][j]==0){count[0]=0;break;}
				else if(c[i+k][j]== cases ){break;}
				else{count[0]++;}		
			}
		}if(count[0]==0 || count[0]==gs-i){count[0]=0;}
		//西向遍历
		if(i!=1){
			for(int k =1 ;k< i ;k++){
				if(c[i-k][j]==0){count[1]=0;break;}
				else if(c[i-k][j]== cases ){break;}
				else{count[1]++;}		
			}
		}if(count[1]==0 || count[1]==i-1){count[1]=0;}
		/**纵向遍历*/
		//南向遍历
		if(j!=gs){
			for(int k =1 ;k< gs-j+1 ;k++){
				if(c[i][j+k]==0){count[2]=0;break;}
				else if(c[i][j+k]== cases ){break;}
				else{count[2]++;}		
			}
		}if(count[2]==0 || count[2]==gs-j){count[2]=0;}
		//北向遍历
		if(j!=1){
			for(int k =1 ;k< j ;k++){
				if(c[i][j-k]==0){count[3]=0;break;}
				else if(c[i][j-k]== cases ){break;}
				else{count[3]++;}		
			}
		}if(count[3]==0 || count[3]==j-1){count[3]=0;}
		/**斜向遍历*/
		//定义四个数代表斜向格数
		int ne,nw,se,sw;
			if(j<Config.ROWS+1-i){ne=j-1;sw=i-1;}else{ne=gs-i;sw=gs-j;}
			if(j<=i){nw=j-1;se=gs-i;}else{nw=i-1;se=gs-j;}
		//东北向遍历
		if(ne!=0){
			for(int k =1 ;k< ne+1 ;k++){
				if(c[i+k][j-k]==0){count[4]=0;break;}
				else if(c[i+k][j-k]== cases ){break;}
				else{count[4]++;}		
			}
		}if(count[4]==0 || count[4]==ne){count[4]=0;}
		//西北向遍历
		if(nw!=0){
			for(int k =1 ;k< nw+1 ;k++){
				if(c[i-k][j-k]==0){count[5]=0;break;}
				else if(c[i-k][j-k]== cases ){break;}
				else{count[5]++;}		
			}
		}if(count[5]==0 || count[5]==nw){count[5]=0;}
		//东南向遍历
		if(se!=0){
			for(int k =1 ;k< se+1 ;k++){
				if(c[i+k][j+k]==0){count[6]=0;break;}
				else if(c[i+k][j+k]== cases ){break;}
				else{count[6]++;}		
			}
		}if(count[6]==0 || count[6]==se){count[6]=0;}
		//西南向遍历
		if(sw!=0){
			for(int k =1 ;k< sw+1 ;k++){
				if(c[i-k][j+k]==0){count[7]=0;break;}
				else if(c[i-k][j+k]== cases ){break;}
				else{count[7]++;}		
			}
		}if(count[7]==0 || count[7]==sw){count[7]=0;}
	}	

 
      这里的count数组在之后的判断以及改变颜色时会用到。接下来是判

 

 

断了。遍历所得的count(i)代表八个方向中对每个方向而言在可下的情况

下所夹对方棋子数，若不可下，则为零。也就是说，只有当八个方向判定

都不可下时，该处信息才为false。于是有：

/**判断某点对当前子来说是否可下的方法*/
	public void ifcan(int i,int j){
		this.counts(i,j);
		int temp = 0;
		for(int t=0; t<8; t++){
			 temp = temp + count[t];	
		}if(temp==0){
			ifcan[i][j]=false;
		}else{
			ifcan[i][j]=true;cnt_t++;
		}
		/**最后将count数组置零，进行下一次判断*/
		for(int t=0; t<8; t++){
			count[t] = 0;
			}
	}

 
      下完子的同时要翻转中间的棋子，通过刚才得到的count数组，可以

 

 

很快写好，虽然每种都要写一遍，但原理是一样的。

/**改变颜色的方法*/
	public void change(int x, int y){
	
		//调用遍历的方法
		this.counts(x, y);
		
		if(count[0]!=0){
			for(int i=1;i<count[0]+1;i++){
				c[x+i][y]=cases;
				this.chessput(x+i, y);
			}
		}if(count[1]!=0){
			for(int i=1;i<count[1]+1;i++){
				c[x-i][y]=cases;
				this.chessput(x-i, y);
			}
		}if(count[2]!=0){
			for(int i=1;i<count[2]+1;i++){
				c[x][y+i]=cases;
				this.chessput(x, y+i);
			}
		}if(count[3]!=0){
			for(int i=1;i<count[3]+1;i++){
				c[x][y-i]=cases;
				this.chessput(x, y-i);
			}
		}if(count[4]!=0){
			for(int i=1;i<count[4]+1;i++){
				c[x+i][y-i]=cases;
				this.chessput(x+i, y-i);
			}
		}if(count[5]!=0){
			for(int i=1;i<count[5]+1;i++){
				c[x-i][y-i]=cases;
				this.chessput(x-i, y-i);
			}
		}if(count[6]!=0){
			for(int i=1;i<count[6]+1;i++){
				c[x+i][y+i]=cases;
				this.chessput(x+i, y+i);
			}
		}if(count[7]!=0){
			for(int i=1;i<count[7]+1;i++){
				c[x-i][y+i]=cases;
				this.chessput(x-i, y+i);
			}
		}
		for(int t=0; t<8; t++){
			count[t] = 0;
		}
		
	}

 
      另外，棋子的画法另用一个类写在了外面，无非是画实心圆而已，这

 

 

样看起来清爽了不少。在下完一个子之后，通过改变cases的值来更换下

棋方，在这里黑方为1，白方为-1。对于棋盘，给每个格子一个棋盘信息，

也是一个二维数组，名为c[][]，黑为1，白为-1，无子为0。可以下棋之

后，则是判断输赢了，黑白棋的判断输赢很简单，即通过最后棋盘中棋子

的个数来判断，多的一方胜。所以，当每下一颗子之后，都要对棋盘进行

遍历以获得盘中每种颜色棋子的个数，以及对即将下子的一方而言可下的

信息。

for(int j=1; j< Config.ROWS; j++){
			for(int i=1; i< Config.COLUMNS; i++){
				if(c[i][j]==1){
					cnt_b++;ifcan[i][j]=false;//黑子个数加一
				}else if(c[i][j]==-1){
					cnt_w++;ifcan[i][j]=false;//白字个数加一
				}else{
					/**无子点确定对下轮cases的ifcan*/
				this.ifcan(i,j);
					}
			}
		}
		count_true = cnt_t; cnt_t=0;//对当前子而言可以下的地方的个数
		count_black = cnt_b; cnt_b=0;
		count_white = cnt_w; cnt_w=0;//总计棋盘中黑白棋的个数
		
		p4.setText("黑棋个数为："+count_black);
		javax.swing.SwingUtilities.updateComponentTreeUI(p4);
		p5.setText("白棋个数为："+count_white);
		javax.swing.SwingUtilities.updateComponentTreeUI(p5);
				
		/**根据个数的判断*/
		if(count_black==0){
			JOptionPane.showMessageDialog(null, "白棋胜！", "结束",JOptionPane.INFORMATION_MESSAGE);//盘中无黑子，白胜
		}if(count_white==0){
			JOptionPane.showMessageDialog(null, "黑棋胜！", "结束",JOptionPane.INFORMATION_MESSAGE);//盘中无白子，黑胜
		}if(count_true==0){
			cases=-cases;
			for(int j=1; j< Config.ROWS; j++){
				for(int i=1; i< Config.COLUMNS; i++){
					if(c[i][j]==0){
						this.ifcan(i,j);
					}
				}
			}
			count_true = cnt_t; cnt_t=0;//对当前子而言可以下的地方的个数
			if(count_true!=0){
				JOptionPane.showMessageDialog(null, "无子可下！", "换一方 ",JOptionPane.INFORMATION_MESSAGE);
			}else{
			if(count_black>count_white){
				JOptionPane.showMessageDialog(null, "黑棋胜！", "结束",JOptionPane.INFORMATION_MESSAGE);
			}else{
				JOptionPane.showMessageDialog(null, "白棋胜！", "结束",JOptionPane.INFORMATION_MESSAGE);
			}
		}
}//棋盘满时，所剩棋子多的一方胜

         到这里，一个简单的人人对战的黑白棋就写好了，之后会写人机对战的智能算法，现在这篇就告一段落了。最后再放张图吧。