Java基础复习笔记09数据结构-哈夫曼树
1. 哈夫曼树
哈夫曼树也称作最优二叉树,当树中的节点带了权重信息了,带权路径长度最小的二叉树叫做最优二叉树。带权路径长度=sum(权重*度)。sum代表每个节点的之和。加入有如下带权重的节点。
权重分别是1、5、8、4。那么关于这些零散的节点,最优二叉树该如何构建呢?
首先先将离散节点从小到大升序排序
第二从离散节点中在挑选排序前两个节点当做一个新的父节点的两个子节点
第三从离散的节点中去除刚刚使用的两个节点
第四重复第二和第三步骤,直到所有离散节点剔除完毕。哈夫曼树就构建完成
用图形演示过程如下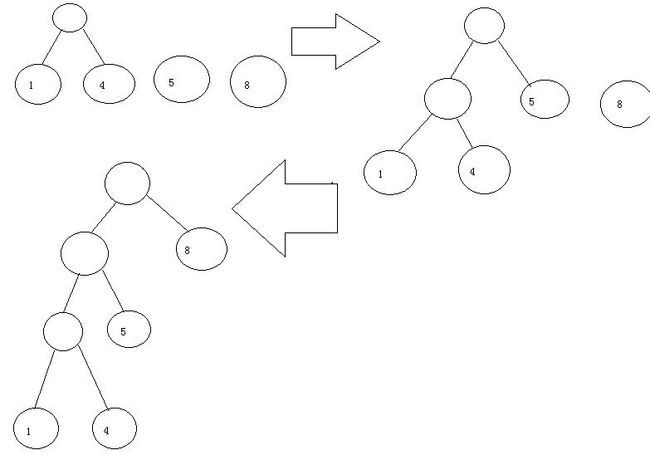
可以看出所有的叶子节点就是之前的离散节点,如果在采用广度遍历法遍历此树。那么遍历的过程实际上就是最短遍历路径的遍历过程
2. 哈夫曼树的使用场景
其实哈夫曼树使用场景还真不少,例如apache负载均衡的按权重请求策略的底层算法、咱们生活中的路由器的路由算法、利用哈夫曼树实现汉字点阵字形的压缩存储(http://www.cnki.com.cn/Article/CJFDTotal-LYGY200504016.htm)、快速检索信息等等底层优化算法,其实核心就是因为目标带有权重、长度远近这类信息才能构建哈夫曼树模型。
3. 实现哈夫曼树
要想实现哈夫曼树其实就是将一堆零散的节点信息构建成一颗最优二叉树,之后再按广度优先遍历它。
实现哈夫曼树其实就是构建哈夫曼树的过程,原理其实上面已经说了,这里再重复一下。
首先先将离散节点从小到大升序排序
第二从离散节点中在挑选排序前两个节点当做一个新的父节点的两个子节点
第三从离散的节点中去除刚刚使用的两个节点
第四重复第二和第三步骤,直到所有离散节点剔除完毕。哈夫曼树就构建完成
代码以及测试程序如下
package dateStructer.tree.huffmanTree;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
/**
* 哈夫曼树
*
* @author liuyan
*/
public class HuffmanTree {
/**
* 节点实体
*/
public static class Node<T> {
// 数据
T data;
// 权重
int power;
Node<T> leftNode;
Node<T> rightNode;
public Node(T data, int power) {
this.data = data;
this.power = power;
}
@Override
public String toString() {
// TODO Auto-generated method stub
return "[data:" + data + " power:" + power + "]";
}
@SuppressWarnings("unchecked")
public boolean compareTo(Node node) {
if (this.power < node.power) {
return true;
}
return false;
}
}
/**
* 将集合将序排序
*
* @param <T>
* @param <E>
*
* @param list
*/
@SuppressWarnings("unchecked")
public static void sort(List<Node> list) {
for (int i = 0; i < list.size() - 1; i++) {
for (int j = i + 1; j < list.size(); j++) {
if (list.get(i).compareTo(list.get(j))) {
// 交换数组中的元素位置
Node node = list.get(i);
list.set(i, list.get(j));
list.set(j, node);
}
}
}
}
/**
* 创建哈夫曼树
*
* @param list
* @return
*/
@SuppressWarnings("unchecked")
public static Node createHuffmanTree(List<Node> list) {
while (list.size() > 1) {
sort(list);
Node left = list.get(list.size() - 1);
Node right = list.get(list.size() - 2);
Node parent = new Node("父节点", left.power + right.power);
parent.leftNode = left;
parent.rightNode = right;
list.remove(list.size() - 1);
list.remove(list.size() - 1);
list.add(parent);
}
return list.get(0);
}
@SuppressWarnings("unchecked")
public static List<Node> deepFirst(Node root) {
List<Node> list = new ArrayList<Node>();
Queue<Node> queue = new ArrayDeque<Node>();
queue.add(root);
while (!queue.isEmpty()) {
list.add(queue.peek());
Node twoLinkNode = queue.poll();
if (twoLinkNode.leftNode != null) {
queue.add(twoLinkNode.leftNode);
}
if (twoLinkNode.rightNode != null) {
queue.add(twoLinkNode.rightNode);
}
}
return list;
}
/**
* @param args
*/
public static void main(String[] args) {
List<Node> list = new ArrayList<Node>();
Node<String> node1 = new Node<String>("东方不败", 8);
Node<String> node2 = new Node<String>("风清扬", 5);
Node<String> node3 = new Node<String>("岳不群", 4);
Node<String> node4 = new Node<String>("左冷禅", 1);
list.add(node1);
list.add(node2);
list.add(node3);
list.add(node4);
Node root = createHuffmanTree(list);
System.out.println(deepFirst(root));
}
}
测试结果是
[[data:父节点 power:18], [data:东方不败 power:8], [data:父节点 power:10], [data:父节点 power:5], [data:风清扬 power:5], [data:左冷禅 power:1], [data:岳不群 power:4]]