获奖感言及我的答案
这次参加博文视点杯[http://www.iteye.com/topic/1119293]有奖答题活动,很高兴自己的答案能够获得评委的认可。
下面发布我的获奖答案,供大家参考,也期待大家能给些意见。谢谢大家。
问题一
一只青蛙一次可以跳上 1 级台阶,也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法。
解题思路:设n级台阶的跳法总数和n的关系为f(n)。很明显当n=1时,f(1)=1,当n=2时,f(2)=2, 跳法为11,2两种。当n>=3时,假设第一次跳1级,则剩下n-1级,n-1级的跳法总数为f(n-1),假设第一次跳2级,则剩下n-2级,n-2级跳法总数为f(n-2),可以看出,当n>=3时,f(n)=f(n-1)+f(n-2)。
程序实现如下:

优化要点:
1、 考虑到性能,不要用递归实现。
2、 用BigInteger实现,而不是long,或者int。
问题二
一只青蛙一次可以跳上1级台阶,也可以跳上2 级……它也可以跳上n 级,此时该青蛙跳上一个n级的台阶总共有多少种跳法?
解题思路:接着问题一的思路,当n>=3时 ,如果第一次跳1级,则剩下为f(n-1),如果第一次跳2级,则剩下为f(n-2),直到第一次跳n-1级,则剩下f(1),另外再加上第一次就跳n级一种情况。因此,总结出公式应该为f(n) = f(1)+f(2)+... +f(n-2) +f(n-1)+1。根据公式可知,f(n-1) = f(1)+f(2)+... +f(n-2) +1,代入f(n)的公式,即为f(n)=f(n-1)+f(n-1)=2f(n-1)。
程序实现如下:

优化要点:
1、 用BigInteger实现,而不是long,或者int。
问题三
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。 请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。 例如下面的二维数组就是每行、每列都递增排序。如果在这个数组中查找数字7,则返回true; 如果查找数字5,由于数组不含有该数字,则返回false。
1 2 8 9
2 4 9 12
4 7 10 13
6 8 11 15
解题思路:由于这个二维数组是有序的,因此可以用采用二分法,确定低位(数组左上角的数,为数组中的最小值)和高位(数组右下角的数,为数组中的最大值),取中间值与要查找的值进行比较,每一次判断尽可能排除最多的元素。设数组低位的坐标为(lowRow,lowCol),高位的坐标为(highRow,highCol).可知中间数的坐标为((lowRow+highRow)/2, (lowCol+highCol)/2).
如下数组,可知中间数为32:

从数组中可以看出,对于数组中的任意一个数,它的左上方的数(不包括本身),肯定小于这个数,它的右下方的数(不包括本身),肯定大于这个数。所以,如果要查找的数小于32,则一次比较,即可排除32右下角的所有数:

当然,可以在第一次判断的时候,首先判断查找的数如果小于低位的数,或者大于高位的数,直接返回false。
其中最重要的是确定二分查找退出的条件,有以下三种情况:
情况一:假设查找的数为27,第一次比较32,27小于32,因此再取9和32的中间数即21,21小于27,因此27在21和32之间,21和32对位相邻,即退出二分查找,这时候,可以知道要找的数只可能位于绿色框内:
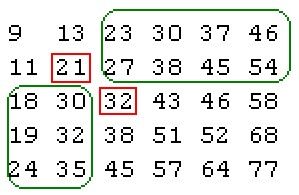
这时候,再递归查找右上角和左下角的两个子数组。
情况二:如下数组查找25:
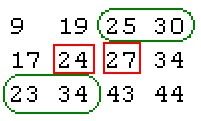
第一次判断中间数24,小于25,因此取24和44中间数27,判断27大于25,此时24和27左右相邻,因此25只可能位于图中绿色框内,再递归查找右上角和左下角的两个子数组。
情况三:如下数组查找27:
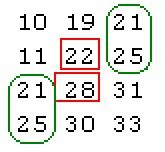
第一次判断中间数22,27大于22,再判断22和33的中间数28,27小于28,此时,22和28上下相邻,因此,要查找的数只可能位于绿色框内,递归查找右上角和左下角的两个子数组。
从上面的分析可知,在不断的二分法查找过程中,高位和低位的位置在不断变化,直到高位和低位上下相邻或者左右相邻或者对角相邻时,退出二分查找,这时候,需要根据高位和低位相邻的种类,取不同的右上角和左下角的子数组,递归查找。在查找过程中,如果在右上角的子数组中找到目标数,则无需再查找左下角的数,直接返回true。另外,在查找过程中,如果发现中间数,或者高位和低位的数和要查找的数相同,那么,即可直接返回true,无需继续查找。
源文件
问题一和问题二源文件:Fog.java
问题三源文件为:BinarySearch.java
下面发布我的获奖答案,供大家参考,也期待大家能给些意见。谢谢大家。
问题一
一只青蛙一次可以跳上 1 级台阶,也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法。
解题思路:设n级台阶的跳法总数和n的关系为f(n)。很明显当n=1时,f(1)=1,当n=2时,f(2)=2, 跳法为11,2两种。当n>=3时,假设第一次跳1级,则剩下n-1级,n-1级的跳法总数为f(n-1),假设第一次跳2级,则剩下n-2级,n-2级跳法总数为f(n-2),可以看出,当n>=3时,f(n)=f(n-1)+f(n-2)。
程序实现如下:

优化要点:
1、 考虑到性能,不要用递归实现。
2、 用BigInteger实现,而不是long,或者int。
问题二
一只青蛙一次可以跳上1级台阶,也可以跳上2 级……它也可以跳上n 级,此时该青蛙跳上一个n级的台阶总共有多少种跳法?
解题思路:接着问题一的思路,当n>=3时 ,如果第一次跳1级,则剩下为f(n-1),如果第一次跳2级,则剩下为f(n-2),直到第一次跳n-1级,则剩下f(1),另外再加上第一次就跳n级一种情况。因此,总结出公式应该为f(n) = f(1)+f(2)+... +f(n-2) +f(n-1)+1。根据公式可知,f(n-1) = f(1)+f(2)+... +f(n-2) +1,代入f(n)的公式,即为f(n)=f(n-1)+f(n-1)=2f(n-1)。
程序实现如下:

优化要点:
1、 用BigInteger实现,而不是long,或者int。
问题三
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。 请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。 例如下面的二维数组就是每行、每列都递增排序。如果在这个数组中查找数字7,则返回true; 如果查找数字5,由于数组不含有该数字,则返回false。
1 2 8 9
2 4 9 12
4 7 10 13
6 8 11 15
解题思路:由于这个二维数组是有序的,因此可以用采用二分法,确定低位(数组左上角的数,为数组中的最小值)和高位(数组右下角的数,为数组中的最大值),取中间值与要查找的值进行比较,每一次判断尽可能排除最多的元素。设数组低位的坐标为(lowRow,lowCol),高位的坐标为(highRow,highCol).可知中间数的坐标为((lowRow+highRow)/2, (lowCol+highCol)/2).
如下数组,可知中间数为32:

从数组中可以看出,对于数组中的任意一个数,它的左上方的数(不包括本身),肯定小于这个数,它的右下方的数(不包括本身),肯定大于这个数。所以,如果要查找的数小于32,则一次比较,即可排除32右下角的所有数:

当然,可以在第一次判断的时候,首先判断查找的数如果小于低位的数,或者大于高位的数,直接返回false。
其中最重要的是确定二分查找退出的条件,有以下三种情况:
情况一:假设查找的数为27,第一次比较32,27小于32,因此再取9和32的中间数即21,21小于27,因此27在21和32之间,21和32对位相邻,即退出二分查找,这时候,可以知道要找的数只可能位于绿色框内:

这时候,再递归查找右上角和左下角的两个子数组。
情况二:如下数组查找25:

第一次判断中间数24,小于25,因此取24和44中间数27,判断27大于25,此时24和27左右相邻,因此25只可能位于图中绿色框内,再递归查找右上角和左下角的两个子数组。
情况三:如下数组查找27:

第一次判断中间数22,27大于22,再判断22和33的中间数28,27小于28,此时,22和28上下相邻,因此,要查找的数只可能位于绿色框内,递归查找右上角和左下角的两个子数组。
从上面的分析可知,在不断的二分法查找过程中,高位和低位的位置在不断变化,直到高位和低位上下相邻或者左右相邻或者对角相邻时,退出二分查找,这时候,需要根据高位和低位相邻的种类,取不同的右上角和左下角的子数组,递归查找。在查找过程中,如果在右上角的子数组中找到目标数,则无需再查找左下角的数,直接返回true。另外,在查找过程中,如果发现中间数,或者高位和低位的数和要查找的数相同,那么,即可直接返回true,无需继续查找。
源文件
问题一和问题二源文件:Fog.java
问题三源文件为:BinarySearch.java