算法 之 堆 - 创建堆
给出一个有n个元素的数组A[1...n],要创建一个包含这些元素的堆,可以这样进行:从空的堆开始,不断插入每一个元素,直到A完全被转移到堆中为止。因为插入第j个键值用时O(log j),因此用这种方法创建堆栈的时间复杂性是O(n log n)。
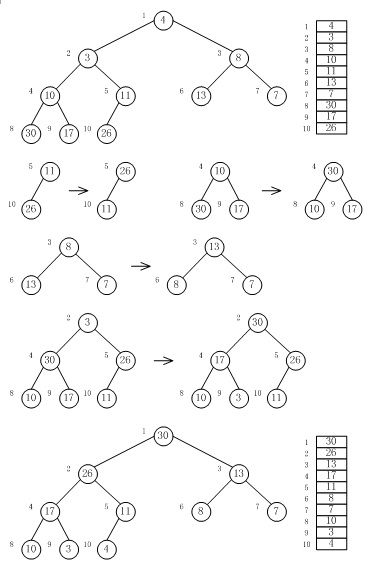
我们知道对应于堆H[1...n]的树的节点可以方便地以自顶向下、从左到右的方式从1到n编码。在这样编码之后,可以用下面的方法,把一棵n个节点的几乎完全的二叉树转换成堆H[1...n]。从最后一个节点开始(编码为n的那一个)到根节点(编码为1的节点),逐个扫描所有的节点,根据需要,每一次将以当前节点为根节点的子树转换成堆。
每一棵只有一片叶子的子树已经是一个堆,因此叶子被跳过。
当以第i个节点为根的子树不是堆时,我们就对i进行Sift-down运算一边把它转换成堆。如此进行下去,使整棵二叉树符合堆得性质。
上面说明了如何对树进行运算。直接对输入的数组执行同样的过程是相当容易的。
令A[1...n]是已知数组,T是对应于A的一棵几乎完全的二叉树,我们注意到 A[⌊n/2⌋+1],A[⌊n/2⌋+2],...,A[n] 它们对应于T的叶子,这样我们可以直接从A[⌊n/2⌋]开始调整数组,然后继续调整 A[⌊n/2⌋-1],A[⌊n/2⌋-2],...,A[1]。这样得到的数组就是我们需要的堆。
过程 MakeHeap
输入 n个元素的数组A[1...n]
输出 A[1...n]转换成堆
算法描述
for i ← ⌊n/2⌋ downto 1
Sift-down(A, i)
end for
注意这里算法描述的数组的索引都是1...n,而不是大家习惯的0...n-1。
下面我们来计算算法MakeHeap的运行时间
设T是对应于数组A[1...n]的一棵几乎完全的二叉树,那么由观察结论可知,T的高是k=⌊log n⌋。
令A[j]对应该树的第i层中第j个节点,当语句Sift-down(A, j)调用过程Sift-down时,重复执行的次数最多是k-i。
因为在第i层上正好有2i个节点,0≤i<k,所以每一层循环执行的总次数的上界是 (k-i)2i。
总的循环执行的总次数的上界就是:
由于在过程Sift-down的每一个循环中,最多有两次元素的比较,因此元素比较的总次数是2×2n=4n。
但是在每次调用Sift-down时,都至少执行一次循环,因此元素比较的最小次数是2⌊n/2⌋≥n-1,这个就是元素比较的总次数的下界。
因此,MakeHeap算法需要Θ(n)时间来构造一个n元素的堆,似乎并不是之前我们认为的O(n log n)时间。
int* makeHeap(int* array, int arrayLength)
{
if (array == NULL || arrayLength <= 0)
return NULL;
int heapLength = arrayLength;
int* heap = (int*)malloc(sizeof(array) * (heapLength + 1));
if (heap == NULL)
return NULL;
// heap[0]用来存储数组中堆数据的长度,堆数据heap[1]...heap[heapLength]
// 所以数组的实际长度是heapLength+1,我们只对从数组索引为1开始的heapLength个数据进行操作
heap[0] = heapLength;
for (int i = 0; i < arrayLength; i++)
{
heap[i + 1] = array[i];
}
for (int i = heapLength / 2; i >= 1; i--)
{
siftDown(heap, i);
}
return heap;
}
我使用的数组是这样定义的:
const int ARRAY_LENGTH = 10;
int array[ARRAY_LENGTH] = { 4, 3, 8, 10, 11, 13, 7, 30, 17, 26 };
// 如果用我上面写的方法创建堆,不要忘了在操作完成之后释放内存哦
int* heap = makeHeap(array, ARRAY_LENGTH);
// do something ...
free(heap);
更多内容请参考: