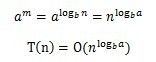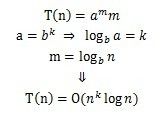《算法引论》之算法分析
上次写博客,已经是半个月之前了。我也不知道我这段日子在干嘛了,没有具体的目标与计划,比较随性,看了几本原本束之高阁的书,包括那本室友推荐,买来后一直搁在床头,不少著名的书里提到的《怎样解题》,以及那本曾经感觉不能理解的《孤独及其所创造的》,还看了一部《中国近代史》,因为还未买到港版,至今还在看小小的手机屏幕。昨夜清风习习,凉意袭人,没有负担,没有烦恼,可以看书看到自然睡,睡觉睡到自然醒,何其的幸福呵。然后又想起被搁置很久的《算法引论》,于是今天又开始阅读了。
第三章《算法分析》主要用于计算算法的复杂度,记得以前《算法导论》也有仔细介绍过,不过没有仔细去了解。关于上界、下界等标记也没有仔细去理解。今天算是认真了一回吧。
首先介绍一下这三个符号:Ο、Ω、Θ
如果存在常数项c和N,使得对于所有的n>=N,有g(n)<=c f(n),则称函数g(n)相对于另一函数f(n)是Ο(f(n)),换句话说,对于足够大的n,函数g(n)不超过函数f(n)的一个固定倍数。Ο是函数的上界。
如果存在常数项c和N,使得对于所有的n>=N,在输入规模为n是解决问题的步数T(n)至少为c g(n),则我们说T(n)=Ω(g(n))。
如果一个特定函数f(n)同时满足f(n)=Ο(g(n))和f(n)=Ω(g(n)),则称f(n)=Θ(g(n))。
符号Ο、Ω、Θ分别大致对应的是"<=",">="和"="。
另外,有如下定理:
1. 对于所有常数c>0和a>1,以及所有单调递增函数f(n),有(f(n))^c = Ο(a^f(n))
换句话说,一个指数函数要比一个多项式函数增长得快。
2. 如果f(n)=Ο(s(n))并且g(n)=Ο(r(n)),则f(n)+g(n)=Ο(s(n)+r(n))
3. 如果f(n)=Ο(s(n))并且g(n)=Ο(r(n)),则f(n).g(n)=Ο(s(n).r(n))
关于算法的复杂度分析,有两种情况:
(1)如果算法由几个部分组成,则它的复杂度通常是这些部分的复杂度的总和。算法可能包含一个执行多次的循环,每一次都有不同的复杂度。这涉及到求和。
(2)分治算法常常把一个大规模的输入递归地分成小规模输入,最后再从小到大整合起来,其算法的复杂度常常具有递推关系。另外,一些算法本身也是递推的,如Fibonacci数列。
熟悉这些将对我们分析算法的复杂度有很大的帮助。
1. 我们知道sum(i)=n(n+1)/2,现在让我们求和:sum(i^2)

2. 分治算法常常具有如下的算法运行时间表达式:
该式的含义为,算法将问题分为a个子问题,每个子问题的规模是原始问题的1/b,用于合并各个子问题的算法运行时间是cn^k。a, b, c, k均为常数。
尝试着把它拆开,假设当n=b^m,且T(1)=c,有:

这是一个简单的几何级数,分三种情况,分别取决于(b^k/a)是大于1, 等于1还是小于1.
情况1:a>b^k
此时,当m趋向于无穷大时,级数收敛于常数。因此T(n)=Ο(a^m),而m=log_b(n),因此有
情况2:a=b^k
情况3:a<b^k
在此情况下,几何级数的因子大于1,为了计算几何级数的和,可以使用标准表达式。用F(F是一个常数)来表示b^k/a,由于级数的第一个元素是a^m,所以有:
再来看一下著名的Fibonacci数列:
F(n)=F(n-1)+F(n-2), F(1)=1, F(2)=2
一个合理的猜测是F(n)每次都被加倍,即它大约为2^n,尝试F(n)=c2^n,则有:
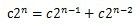
显然c2^n太大了,并且c在等式中并不起作用。我们尝试使用一个小一点的底数a,令F(n)=a^n,则有:
还有一种递推关系,它涉及全部历史,例如:

第三章《算法分析》主要用于计算算法的复杂度,记得以前《算法导论》也有仔细介绍过,不过没有仔细去了解。关于上界、下界等标记也没有仔细去理解。今天算是认真了一回吧。
首先介绍一下这三个符号:Ο、Ω、Θ
如果存在常数项c和N,使得对于所有的n>=N,有g(n)<=c f(n),则称函数g(n)相对于另一函数f(n)是Ο(f(n)),换句话说,对于足够大的n,函数g(n)不超过函数f(n)的一个固定倍数。Ο是函数的上界。
如果存在常数项c和N,使得对于所有的n>=N,在输入规模为n是解决问题的步数T(n)至少为c g(n),则我们说T(n)=Ω(g(n))。
如果一个特定函数f(n)同时满足f(n)=Ο(g(n))和f(n)=Ω(g(n)),则称f(n)=Θ(g(n))。
符号Ο、Ω、Θ分别大致对应的是"<=",">="和"="。
另外,有如下定理:
1. 对于所有常数c>0和a>1,以及所有单调递增函数f(n),有(f(n))^c = Ο(a^f(n))
换句话说,一个指数函数要比一个多项式函数增长得快。
2. 如果f(n)=Ο(s(n))并且g(n)=Ο(r(n)),则f(n)+g(n)=Ο(s(n)+r(n))
3. 如果f(n)=Ο(s(n))并且g(n)=Ο(r(n)),则f(n).g(n)=Ο(s(n).r(n))
关于算法的复杂度分析,有两种情况:
(1)如果算法由几个部分组成,则它的复杂度通常是这些部分的复杂度的总和。算法可能包含一个执行多次的循环,每一次都有不同的复杂度。这涉及到求和。
(2)分治算法常常把一个大规模的输入递归地分成小规模输入,最后再从小到大整合起来,其算法的复杂度常常具有递推关系。另外,一些算法本身也是递推的,如Fibonacci数列。
熟悉这些将对我们分析算法的复杂度有很大的帮助。
1. 我们知道sum(i)=n(n+1)/2,现在让我们求和:sum(i^2)

2. 分治算法常常具有如下的算法运行时间表达式:
该式的含义为,算法将问题分为a个子问题,每个子问题的规模是原始问题的1/b,用于合并各个子问题的算法运行时间是cn^k。a, b, c, k均为常数。
尝试着把它拆开,假设当n=b^m,且T(1)=c,有:

这是一个简单的几何级数,分三种情况,分别取决于(b^k/a)是大于1, 等于1还是小于1.
情况1:a>b^k
此时,当m趋向于无穷大时,级数收敛于常数。因此T(n)=Ο(a^m),而m=log_b(n),因此有
情况2:a=b^k
情况3:a<b^k
在此情况下,几何级数的因子大于1,为了计算几何级数的和,可以使用标准表达式。用F(F是一个常数)来表示b^k/a,由于级数的第一个元素是a^m,所以有:
再来看一下著名的Fibonacci数列:
F(n)=F(n-1)+F(n-2), F(1)=1, F(2)=2
一个合理的猜测是F(n)每次都被加倍,即它大约为2^n,尝试F(n)=c2^n,则有:
显然c2^n太大了,并且c在等式中并不起作用。我们尝试使用一个小一点的底数a,令F(n)=a^n,则有:
还有一种递推关系,它涉及全部历史,例如: