一种理想的在关系数据库中存储树型结构数据的方法

一种理想的在关系数据库中存储树型结构数据的方法
2008-06-24 17:05 by Jacky_Xu, 1553 visits, 网摘, 收藏, 编辑
在各种基于关系数据库的应用系统开发中，我们往往需要存储树型结构的数据，目前有很多流行的方法，如邻接列表模型（The Adjacency List Model），在此基础上也有很多人针对不同的需求做了相应的改进，但总是在某些方面存在的各种各样的缺陷。
    那么理想中的树型结构应具备哪些特点呢？数据存储冗余小、直观性强；方便返回整个树型结构数据；可以很轻松的返回某一子树（方便分层加载）；快整获以某节 点的祖谱路径；插入、删除、移动节点效率高等等。带着这些需求我查找了很多资料，发现了一种理想的树型结构数据存储及操作算法，改进的前序遍历树模型 （The Nested Set Model）。
一、数据

    在本文中，举一个在线食品店树形图的例子。这个食品店通过类别、颜色和品种来组织食品。树形图如下：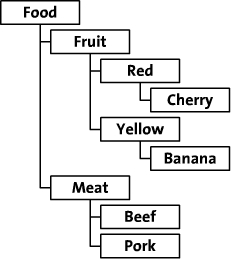


 

二、邻接列表模型（The Adjacency List Model）

在这种模型下，上述数据在关系数据库的表结构数据通常如下图所示：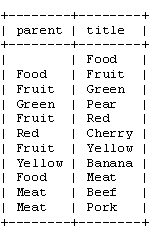



 
由于该模型比较简单，在此不再详细介绍其算法，下面列出它的一些不足：

    在大多数编程语言中，他运行很慢，效率很差。这主要是“递归”造成的。我们每次查询节点都要访问数据库。每次数据库查询都要花费一些时间，这让函数处理庞 大的树时会十分慢。造成这个函数不是太快的第二个原因可能是你使用的语言。不像Lisp这类语言，大多数语言不是针对递归函数设计的。对于每个节点造成这 个函数不是太快的第二个原因可能是你使用的语言。不像Lisp这类语言，大多数语言不是针对递归函数设计的。对于每个节点，函数都要调用他自己，产生新的 实例。这样，对于一个4层的树，你可能同时要运行4个函数副本。对于每个函数都要占用一块内存并且需要一定的时间初始化，这样处理大树时递归就很慢了。

三、改进的前序遍历树模型（The Nested Set Model）

原理：

    我们先把树按照水平方式摆开。从根节点开始（“Food”），然后他的左边写上1。然后按照树的顺序（从上到下）给“Fruit”的左边写上2。这样，你 沿着树的边界走啊走（这就是“遍历”），然后同时在每个节点的左边和右边写上数字。最后，我们回到了根节点“Food”在右边写上18。下面是标上了数字 的树，同时把遍历的顺序用箭头标出来了。


 

    我们称这些数字为左值和右值（如，“Food”的左值是1，右值是18）。正如你所见，这些数字按时了每个节点之间的关系。因为“Red”有3和6两个 值，所以，它是有拥有1-18值的“Food”节点的后续。同样的，我们可以推断所有左值大于2并且右值小于11的节点，都是有2-11的“Fruit” 节点的后续。这样，树的结构就通过左值和右值储存下来了。这种数遍整棵树算节点的方法叫做“改进前序遍历树”算法。

表结构设计：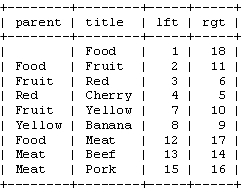



 
常用的操作：

下面列出一些常用操作的SQL语句

返回完整的树（Retrieving a Full Tree）
SELECT node.name
  FROM nested_category node, nested_category parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
   AND parent.name = 'electronics'
ORDER BY node.lft

返回某结点的子树（Find the Immediate Subordinates of a Node）
SELECT V.*
  FROM (SELECT node.name,
               (COUNT(parent.name) - (AVG(sub_tree.depth) + 1)) depth
          FROM nested_category node,
               nested_category parent,
               nested_category sub_parent,
               (SELECT V.*
                  FROM (SELECT node.name, (COUNT(parent.name) - 1) depth
                          FROM nested_category node, nested_category parent
                         WHERE node.lft BETWEEN parent.lft AND parent.rgt
                           AND node.name = 'portable electronics'
                         GROUP BY node.name) V,
                       nested_category T
                 WHERE V.name = T.name
                 ORDER BY T.lft) sub_tree
         WHERE node.lft BETWEEN parent.lft AND parent.rgt
           AND node.lft BETWEEN sub_parent.lft AND sub_parent.rgt
           AND sub_parent.name = sub_tree.name
         GROUP BY node.name) V,
       nested_category T
WHERE V.name = T.name
   and V.depth <= 1
   and V.depth > 0
ORDER BY T.Lft

返回某结点的祖谱路径（Retrieving a Single Path）
SELECT parent.name
  FROM nested_category node, nested_category parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
   AND node.name = 'flash'
ORDER BY node.lft

返回所有节点的深度（Finding the Depth of the Nodes）
SELECT V.*
  FROM (SELECT node.name, (COUNT(parent.name) - 1) depth
          FROM nested_category node, nested_category parent
         WHERE node.lft BETWEEN parent.lft AND parent.rgt
         GROUP BY node.name) V,
       nested_category T
WHERE V.name = T.name
ORDER BY T.Lft

返回子树的深度（Depth of a Sub-Tree）
SELECT V.*
  FROM (SELECT node.name,
               (COUNT(parent.name) - (AVG(sub_tree.depth) + 1)) depth
          FROM nested_category node,
               nested_category parent,
               nested_category sub_parent,
               (SELECT V.*
                  FROM (SELECT node.name, (COUNT(parent.name) - 1) depth
                          FROM nested_category node, nested_category parent
                         WHERE node.lft BETWEEN parent.lft AND parent.rgt
                           AND node.name = 'portable electronics'
                         GROUP BY node.name) V,
                       nested_category T
                 WHERE V.name = T.name
                 ORDER BY T.lft) sub_tree
         WHERE node.lft BETWEEN parent.lft AND parent.rgt
           AND node.lft BETWEEN sub_parent.lft AND sub_parent.rgt
           AND sub_parent.name = sub_tree.name
         GROUP BY node.name) V,
       nested_category T
WHERE V.name = T.name
ORDER BY T.Lft

返回所有的叶子节点（Finding all the Leaf Nodes）
SELECT name FROM nested_category WHERE rgt = lft + 1

插入节点（Adding New Nodes）
LOCK TABLE nested_category WRITE;

SELECT @myRight := rgt FROM nested_category WHERE name = 'TELEVISIONS';

UPDATE nested_category SET rgt = rgt + 2 WHERE rgt > @myRight;
UPDATE nested_category SET lft = lft + 2 WHERE lft > @myRight;

INSERT INTO nested_category
  (name, lft, rgt)
VALUES
  ('GAME CONSOLES', @myRight + 1, @myRight + 2);

UNLOCK TABLES;

删除节点（Deleting Nodes）
LOCK TABLE nested_category WRITE;

SELECT @myLeft := lft, @myRight := rgt, @myWidth := rgt - lft + 1
  FROM nested_category
WHERE name = 'GAME CONSOLES';

DELETE FROM nested_category WHERE lft BETWEEN @myLeft AND @myRight;

UPDATE nested_category SET rgt = rgt - @myWidth WHERE rgt > @myRight;
UPDATE nested_category SET lft = lft - @myWidth WHERE lft > @myRight;

UNLOCK TABLES;

 

 

 

 

以上属于转载

 

这种树形结构与查询有利，但在作节点位置修改时耗费巨大，最差的算法，你得把一棵树的节点序号统统修改个遍，因此凡事有利有弊