- CentOS的根目录下,/bin 和 /sbin 用途和权限
Energet!c
Linux日常centoslinux运维
CentOS的根目录下,/bin和/sbin用途和权限一、/bin(Binary)二、/sbin(SystemBinary)三、总结在CentOS的根目录下,/bin和/sbin目录有不同的用途和权限一、/bin(Binary)用途:存放系统的基本命令,这些命令对所有用户都是可用的。例如:ls、cp、mv、rm等。权限:普通用户和系统管理员都可以使用这些命令。二、/sbin(SystemBinar
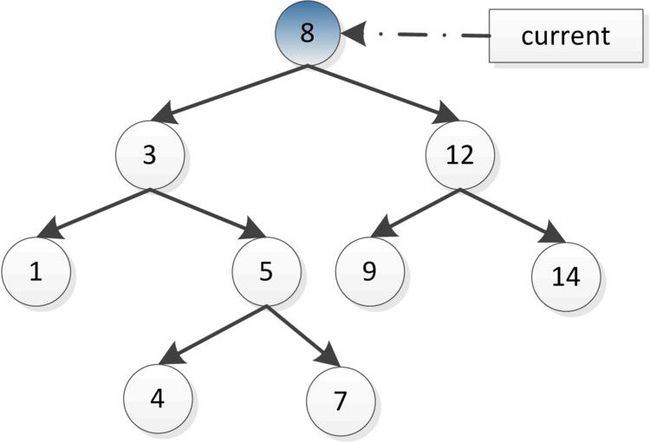
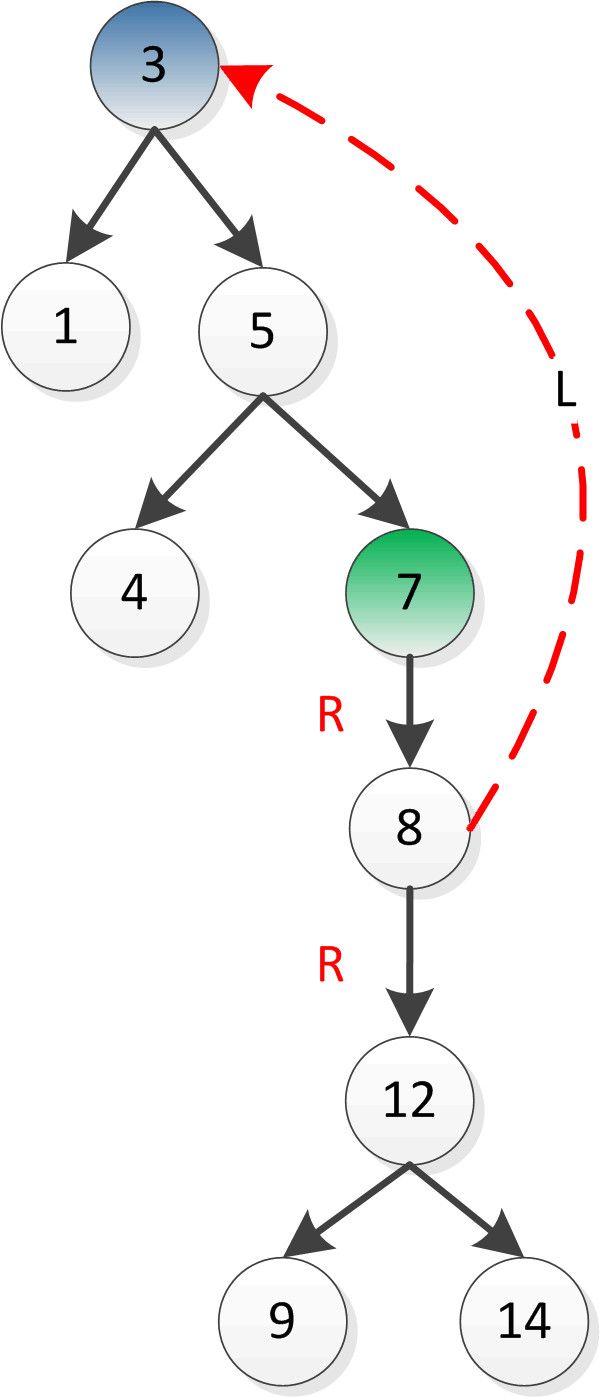
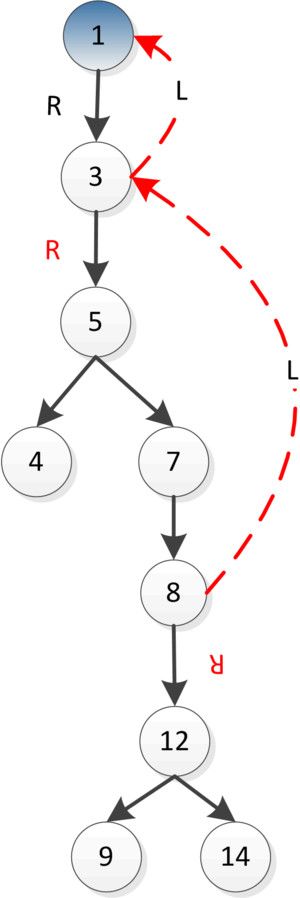
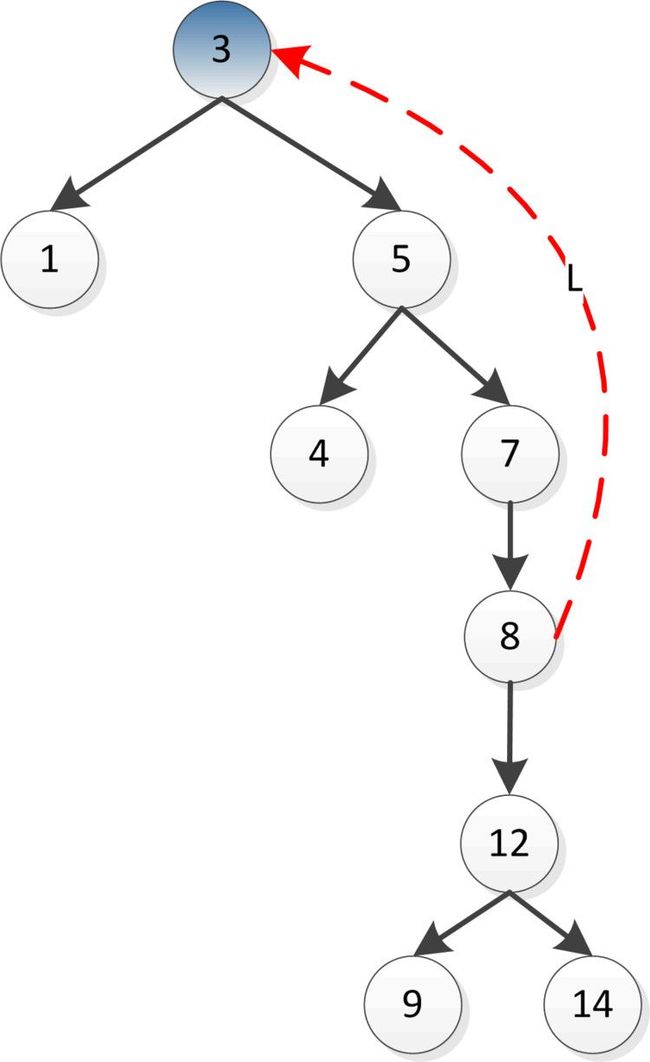
- 《 C++ 修炼全景指南:九 》打破编程瓶颈!掌握二叉搜索树的高效实现与技巧
Lenyiin
C++修炼全景指南技术指南c++算法stl
摘要本文详细探讨了二叉搜索树(BinarySearchTree,BST)的核心概念和技术细节,包括插入、查找、删除、遍历等基本操作,并结合实际代码演示了如何实现这些功能。文章深入分析了二叉搜索树的性能优势及其时间复杂度,同时介绍了前驱、后继的查找方法等高级功能。通过自定义实现的二叉搜索树类,读者能够掌握其实际应用,此外,文章还建议进一步扩展为平衡树(如AVL树、红黑树)以优化极端情况下的性能退化。
- leetcode-124 Binary Tree Maximum Path Sum
乐观的大鹏
LeetCode
Givenanon-emptybinarytree,findthemaximumpathsum.Forthisproblem,apathisdefinedasanysequenceofnodesfromsomestartingnodetoanynodeinthetreealongtheparent-childconnections.Thepathmustcontainatleastonenodea
- 单节点canal的介绍和搭建(对接mysql和rocketMQ)
汀风
中间件阿里云mysqljava
单节点canal-server+canal-admin的介绍和搭建(对接mysql和rocketMQ)一、简介1、Canal1、工作原理2、MySQL主从复制实现3、canal架构4、binarylog1、新增binlog2、更新binglog3、增加字段bin-log4、删除字段bin-log5、修改字段bin-log二、使用2.1安装1、本地安装2、docker安装canal-admincan
- excel表格解析数据
摸鱼的张三
exceljava前端
varpersons=[];functionexcelChange(e){varfiles=e.filesvarfileReader=newFileReader();fileReader.onload=function(ev){console.log(ev);vardata=ev.target.resultvarworkbook=XLSX.read(data,{type:'binary'})var
- ARM-Cortex-M架构:1、STM32函数参数传递
天城寺电子
嵌入式软件开发arm开发stm32汇编C语言
文章目录参数传递概览堆栈传递参数具体过程参数传递概览在调用子函数时,ARMCortex-M3处理器可以使用寄存器和堆栈来传递参数。具体使用哪种方式取决于传递的参数数量和调用约定(callingconvention)。参数传递方式ARMCortex-M3处理器使用ARMEABI(EmbeddedApplicationBinaryInterface)标准来定义参数传递的约定。根据这个约定:1、寄存器传
- python读二进制数据,Python二进制数据读取
上山下海何小妞
python读二进制数据
Aurllib2requestreceivesbinaryresponseasbelow:000000010004414D544400000000024197333341995C2941903D714191D70A470FC614000001166AE068804193B40541971EB841907AE141968F5746E62E80000001167A537C80FFFFItsstruct
- Unity数据持久化 之 一个通过2进制读取Excel并存储的轮子(5) 表加载
咩咩觉主
Unity滚滚车轮计划Unity案例实战全解析Unity数据持久化开发语言unityc#游戏引擎
太狠了,有很多地方我还没搞明白usingSystem;usingSystem.Collections;usingSystem.Collections.Generic;usingSystem.IO;usingSystem.Reflection;usingSystem.Runtime.Serialization.Formatters.Binary;usingSystem.Text;usingUnity
- MySql关键字
zm2714
mysql
ADDALLALTERANALYZEANDASASCASENSITIVEBEFOREBETWEENBIGINTBINARYBLOBBOTHBYCALLCASCADECASECHANGECHARCHARACTERCHECKCOLLATECOLUMNCONDITIONCONNECTIONCONSTRAINTCONTINUECONVERTCREATECROSSCURRENT_DATECURRENT_TI
- LeetCode | 0235. 二叉搜索树的最近公共祖先【Python】
Wonz
ProblemLeetCodeGivenabinarysearchtree(BST),findthelowestcommonancestor(LCA)oftwogivennodesintheBST.AccordingtothedefinitionofLCAonWikipedia:“Thelowestcommonancestorisdefinedbetweentwonodespandqasthelo
- LeetCode之二叉搜索树
星夜孤帆
leetcode算法
530.二叉搜索树的最小绝对差/***Definitionforabinarytreenode.*publicclassTreeNode{*intval;*TreeNodeleft;*TreeNoderight;*TreeNode(){}*TreeNode(intval){this.val=val;}*TreeNode(intval,TreeNodeleft,TreeNoderight){*thi
- MySQL 大小写问题
天珩
今日所得
场景在做mysql查询的时候,注意到一个问题,mysql默认是不区分大小写的通过简单的查询,发现通过关键字binary可以强制区分大小写参考每日所得--分页查询优化和mysql区分大小写问题那为什么MySQL不区分大小写呢参考文档mysql不区分大小写技术原理文章总结1、是否区分是取决于字符集和校对(Collation)部分所做的工作2、取决于字符集中是否声明了大小写敏感声明之后,开销增加参考ht
- AttributeError: ‘tuple‘ object has no attribute ‘shape‘
晓胡同学
keras深度学习tensorflow
AttributeError:‘tuple’objecthasnoattribute‘shape’在将keras代码改为tensorflow2代码的时候报了如下错误AttributeError:'tuple'objecthasnoattribute'shape'经过调查发现,损失函数写错了原来的是这样model.compile(loss=['binary_crossentropy'],optimi
- 数据结构--二叉树(C语言实现,超详细!!!)
鲁鲁修•vi•不列颠尼亚
数据结构c语言算法
文章目录二叉树的概念代码实现二叉树的定义创建一棵树并初始化组装二叉树前序遍历中序遍历后序遍历计算树的结点个数求二叉树第K层的结点个数求二叉树高度查找X所在的结点查找指定节点在不在完整代码二叉树的概念二叉树(BinaryTree)是数据结构中一种非常重要的树形结构,它的特点是每个节点最多有两个子节点,通常称为左子节点和右子节点。这种结构使得二叉树在数据存储和查找等方面具有高效性,广泛应用于各种算法和
- Python 二分法查找
swiftshow
pythonpythonlist
1.如果找到该值就返回2.如果找不到该值就返回该值的上一个Index和下一个Index3.小于List[0]返回04.大于len(List)返回该List[-1]defBinarySearch(keyTime,List):low=0high=len(List)-1middle=0while(lowkeyTime:high=middle-1ifhighlen(List)-1:print'超出List
- 数据结构07
speop
数据结构
文章目录二叉树的坡度二叉树的右视图二叉树的坡度/***Definitionforabinarytreenode.*structTreeNode{*intval;*TreeNode*left;*TreeNode*right;*TreeNode():val(0),left(nullptr),right(nullptr){}*TreeNode(intx):val(x),left(nullptr),rig
- Detecting Memory Management and Threading Bugs with Valgrind
Chia-Te Kuan
分析工具交叉編譯經驗談elasticsearch大数据搜索引擎git
contentAboutValgrindInstallingValgrindFromSourceFromPre-compiledBinaryPrepareFWandstandardlibrarywithsymbolPrepareFWPreparesysrootonNFSSetLD_LIBRARY_PATHandcreatesymboliclinksPrepareself-implementlibr
- 图片地址携带blob:的原因
J不A秃V头A
前端前端
图片地址携带blob:的原因与Blob对象(BinaryLargeObject)的使用有关。Blob对象代表了一个不可变的、原始数据的类文件对象,通常用于处理二进制数据,如图片、视频或音频文件等。在计算机中,Blob常用于数据库中存储二进制文件,但在Web开发中,Blob对象也被广泛用于前端处理二进制数据。具体来说,当图片地址携带blob:时,这通常意味着图片数据是以Blob对象的形式存储在浏览器
- sumo与python联合进行交通流控制第一步
Britney838
pythonjava前端
先导入必要的安装包fromsumolibimportcheckBinaryimporttraci定位好sumo-gui可视化界面的位置和仿真配置文件的位置sumoBinary="D:/sumo1.19.0/bin/sumo-gui"sumoConfig="D:/sumo1.19.0/file/1.sumocfg"利用traci接口打开配置文件traci.start([sumoBinary,"-c"
- C++ 二进制方式读取和存储图片文件
iummature
c++开发语言
#include"stdafx.h"#include#include#include#include#include#include#includeintmain(){FILE*fp;//1.二进制打开图片文件ifstreamis("D:/workplace/test.jpg",ifstream::in|ios::binary);//2.计算图片长度is.seekg(0,is.end);intle
- Python | Leetcode Python题解之第257题二叉树的所有路径
Mopes__
分享PythonLeetcode题解
题目:题解:classSolution:defbinaryTreePaths(self,root:TreeNode)->List[str]:paths=list()ifnotroot:returnpathsnode_queue=collections.deque([root])path_queue=collections.deque([str(root.val)])whilenode_queue:
- Milvus 核心设计 (4) ---- metric及index原理详解与示例(2)
PhoenixAI8
RAGMilvusChroma源码及实践milvuspython机器学习vectordb人工智能
目录背景BinaryEmbedding定义与特点常见算法应用场景距离丈量的方式JaccardHamming代码实现IndexBIN_FLATBIN_IVF_FLATSparseembeddings定义应用场景优点实现方式距离丈量方式IPIndexSPARSE_INVERTED_INDEX应用场景优势SPARSE_WAND工作原理性能特点应用场景小结背景接着上面的Milvusmetric及index
- 【深入理解计算机系统】 三:布尔逻辑与组合电路
Geeksongs
javascriptvuejqueryjavaspringboot
4.1.BooleanExpressionsToday’sdigitalcircuitsarebuiltsothattheycanperformveryfastoperationsoverdatathatisencodedinbinary.TheunderlyingoperationsarepartofwhatisknownasBooleanAlgebra.Thisalgebraconsistso
- npm配置淘宝镜像仓库以及electron镜像
IT宝哥哥
需要配置淘宝npm镜像仅需在用户目录下~/.npmrc配置如下键值对便可。registry=https://registry.npm.taobao.orgsass_binary_site=https://npm.taobao.org/mirrors/node-sass/electron_mirror=https://npm.taobao.org/mirrors/electron/该项主要针对于有些
- Java算法之判断平衡二叉树
持续输出...
#Java算法算法
判断一棵二叉树是否是平衡二叉树(即AVL树)是一个常见的问题。平衡二叉树的定义是:对于树中的每个节点,其左右子树的高度差不超过1。我们可以通过递归的方法来判断一棵二叉树是否是平衡的packagecom.huawei.od.huawei.algorithm;/***@ClassName:IsBalancedBinaryTree是否是平衡二叉树*@Desc:判断一棵二叉树是否是平衡二叉树(即AVL树)
- python怎么用while函数10进制转二进制?
是先生了
Python学习Python小题python算法
在Python中,while循环通常用于在特定条件为真时重复执行代码块。但是,对于将十进制数转换为二进制数,更常见的方法是使用除法和取余运算,或者使用内置的bin()函数。不过,为了展示如何使用while循环来实现这一转换,下面是一个简单的示例:defdecimal_to_binary(n):ifn==0:return'0'binary=''whilen>0:#取出当前位的值(0或1)binary
- 最全金融数据_PySpark-3(2),大数据开发学习的三个终极问题及学习路线规划
2401_84185145
大数据面试学习
既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上大数据知识点,真正体系化!由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新需要这份系统化资料的朋友,可以戳这里获取frompyspark.ml.evaluationimportBinaryClassificationEv
- unique-binary-search-trees-ii
DaiMorph
classSolution{public:vectorgenerateTrees(intn){returncreate(1,n);}vectorcreate(intL,intR){vectorres;if(L>R){res.push_back(NULL);returnres;}for(inti=L;iLeft=create(L,i-1);vectorRight=create(i+1,R);for(
- Leetcode 662. Maximum Width of Binary Tree
SnailTyan
文章作者:Tyan博客:noahsnail.com|CSDN|1.DescriptionMaximumWidthofBinaryTree2.Solution/***Definitionforabinarytreenode.*structTreeNode{*intval;*TreeNode*left;*TreeNode*right;*TreeNode(intx):val(x),left(NULL),
- C# —— 序列化与反序列化
人狮子
C#c#
概念序列化通过使用不同的类(BinaryFormatter,SoapFormatter,XmlSerializer)将对象状态转换为可保持或传输的格式的过程,具体是将对象转变为字节流,其目的是为了保存数据的状态,方便后续还原调用。包括三种序列化形式:二进制序列化,SOAP序列化,XML序列化。于此过程相反,将序列化文件转换为对象的过程称为反序列化。区别二进制和SOAP格式可序列化所有可序列化字段,
- java封装继承多态等
麦田的设计者
javaeclipsejvmcencapsulatopn
最近一段时间看了很多的视频却忘记总结了,现在只能想到什么写什么了,希望能起到一个回忆巩固的作用。
1、final关键字
译为:最终的
&
- F5与集群的区别
bijian1013
weblogic集群F5
http请求配置不是通过集群,而是F5;集群是weblogic容器的,如果是ejb接口是通过集群。
F5同集群的差别,主要还是会话复制的问题,F5一把是分发http请求用的,因为http都是无状态的服务,无需关注会话问题,类似
- LeetCode[Math] - #7 Reverse Integer
Cwind
java题解MathLeetCodeAlgorithm
原题链接:#7 Reverse Integer
要求:
按位反转输入的数字
例1: 输入 x = 123, 返回 321
例2: 输入 x = -123, 返回 -321
难度:简单
分析:
对于一般情况,首先保存输入数字的符号,然后每次取输入的末位(x%10)作为输出的高位(result = result*10 + x%10)即可。但
- BufferedOutputStream
周凡杨
首先说一下这个大批量,是指有上千万的数据量。
例子:
有一张短信历史表,其数据有上千万条数据,要进行数据备份到文本文件,就是执行如下SQL然后将结果集写入到文件中!
select t.msisd
- linux下模拟按键输入和鼠标
被触发
linux
查看/dev/input/eventX是什么类型的事件, cat /proc/bus/input/devices
设备有着自己特殊的按键键码,我需要将一些标准的按键,比如0-9,X-Z等模拟成标准按键,比如KEY_0,KEY-Z等,所以需要用到按键 模拟,具体方法就是操作/dev/input/event1文件,向它写入个input_event结构体就可以模拟按键的输入了。
linux/in
- ContentProvider初体验
肆无忌惮_
ContentProvider
ContentProvider在安卓开发中非常重要。与Activity,Service,BroadcastReceiver并称安卓组件四大天王。
在android中的作用是用来对外共享数据。因为安卓程序的数据库文件存放在data/data/packagename里面,这里面的文件默认都是私有的,别的程序无法访问。
如果QQ游戏想访问手机QQ的帐号信息一键登录,那么就需要使用内容提供者COnte
- 关于Spring MVC项目(maven)中通过fileupload上传文件
843977358
mybatisspring mvc修改头像上传文件upload
Spring MVC 中通过fileupload上传文件,其中项目使用maven管理。
1.上传文件首先需要的是导入相关支持jar包:commons-fileupload.jar,commons-io.jar
因为我是用的maven管理项目,所以要在pom文件中配置(每个人的jar包位置根据实际情况定)
<!-- 文件上传 start by zhangyd-c --&g
- 使用svnkit api,纯java操作svn,实现svn提交,更新等操作
aigo
svnkit
原文:http://blog.csdn.net/hardwin/article/details/7963318
import java.io.File;
import org.apache.log4j.Logger;
import org.tmatesoft.svn.core.SVNCommitInfo;
import org.tmateso
- 对比浏览器,casperjs,httpclient的Header信息
alleni123
爬虫crawlerheader
@Override
protected void doGet(HttpServletRequest req, HttpServletResponse res) throws ServletException, IOException
{
String type=req.getParameter("type");
Enumeration es=re
- java.io操作 DataInputStream和DataOutputStream基本数据流
百合不是茶
java流
1,java中如果不保存整个对象,只保存类中的属性,那么我们可以使用本篇文章中的方法,如果要保存整个对象 先将类实例化 后面的文章将详细写到
2,DataInputStream 是java.io包中一个数据输入流允许应用程序以与机器无关方式从底层输入流中读取基本 Java 数据类型。应用程序可以使用数据输出流写入稍后由数据输入流读取的数据。
- 车辆保险理赔案例
bijian1013
车险
理赔案例:
一货运车,运输公司为车辆购买了机动车商业险和交强险,也买了安全生产责任险,运输一车烟花爆竹,在行驶途中发生爆炸,出现车毁、货损、司机亡、炸死一路人、炸毁一间民宅等惨剧,针对这几种情况,该如何赔付。
赔付建议和方案:
客户所买交强险在这里不起作用,因为交强险的赔付前提是:“机动车发生道路交通意外事故”;
如果是交通意外事故引发的爆炸,则优先适用交强险条款进行赔付,不足的部分由商业
- 学习Spring必学的Java基础知识(5)—注解
bijian1013
javaspring
文章来源:http://www.iteye.com/topic/1123823,整理在我的博客有两个目的:一个是原文确实很不错,通俗易懂,督促自已将博主的这一系列关于Spring文章都学完;另一个原因是为免原文被博主删除,在此记录,方便以后查找阅读。
有必要对
- 【Struts2一】Struts2 Hello World
bit1129
Hello world
Struts2 Hello World应用的基本步骤
创建Struts2的Hello World应用,包括如下几步:
1.配置web.xml
2.创建Action
3.创建struts.xml,配置Action
4.启动web server,通过浏览器访问
配置web.xml
<?xml version="1.0" encoding="
- 【Avro二】Avro RPC框架
bit1129
rpc
1. Avro RPC简介 1.1. RPC
RPC逻辑上分为二层,一是传输层,负责网络通信;二是协议层,将数据按照一定协议格式打包和解包
从序列化方式来看,Apache Thrift 和Google的Protocol Buffers和Avro应该是属于同一个级别的框架,都能跨语言,性能优秀,数据精简,但是Avro的动态模式(不用生成代码,而且性能很好)这个特点让人非常喜欢,比较适合R
- lua set get cookie
ronin47
lua cookie
lua:
local access_token = ngx.var.cookie_SGAccessToken
if access_token then
ngx.header["Set-Cookie"] = "SGAccessToken="..access_token.."; path=/;Max-Age=3000"
end
- java-打印不大于N的质数
bylijinnan
java
public class PrimeNumber {
/**
* 寻找不大于N的质数
*/
public static void main(String[] args) {
int n=100;
PrimeNumber pn=new PrimeNumber();
pn.printPrimeNumber(n);
System.out.print
- Spring源码学习-PropertyPlaceholderHelper
bylijinnan
javaspring
今天在看Spring 3.0.0.RELEASE的源码,发现PropertyPlaceholderHelper的一个bug
当时觉得奇怪,上网一搜,果然是个bug,不过早就有人发现了,且已经修复:
详见:
http://forum.spring.io/forum/spring-projects/container/88107-propertyplaceholderhelper-bug
- [逻辑与拓扑]布尔逻辑与拓扑结构的结合会产生什么?
comsci
拓扑
如果我们已经在一个工作流的节点中嵌入了可以进行逻辑推理的代码,那么成百上千个这样的节点如果组成一个拓扑网络,而这个网络是可以自动遍历的,非线性的拓扑计算模型和节点内部的布尔逻辑处理的结合,会产生什么样的结果呢?
是否可以形成一种新的模糊语言识别和处理模型呢? 大家有兴趣可以试试,用软件搞这些有个好处,就是花钱比较少,就算不成
- ITEYE 都换百度推广了
cuisuqiang
GoogleAdSense百度推广广告外快
以前ITEYE的广告都是谷歌的Google AdSense,现在都换成百度推广了。
为什么个人博客设置里面还是Google AdSense呢?
都知道Google AdSense不好申请,这在ITEYE上也不是讨论了一两天了,强烈建议ITEYE换掉Google AdSense。至少,用一个好申请的吧。
什么时候能从ITEYE上来点外快,哪怕少点
- 新浪微博技术架构分析
dalan_123
新浪微博架构
新浪微博在短短一年时间内从零发展到五千万用户,我们的基层架构也发展了几个版本。第一版就是是非常快的,我们可以非常快的实现我们的模块。我们看一下技术特点,微博这个产品从架构上来分析,它需要解决的是发表和订阅的问题。我们第一版采用的是推的消息模式,假如说我们一个明星用户他有10万个粉丝,那就是说用户发表一条微博的时候,我们把这个微博消息攒成10万份,这样就是很简单了,第一版的架构实际上就是这两行字。第
- 玩转ARP攻击
dcj3sjt126com
r
我写这片文章只是想让你明白深刻理解某一协议的好处。高手免看。如果有人利用这片文章所做的一切事情,盖不负责。 网上关于ARP的资料已经很多了,就不用我都说了。 用某一位高手的话来说,“我们能做的事情很多,唯一受限制的是我们的创造力和想象力”。 ARP也是如此。 以下讨论的机子有 一个要攻击的机子:10.5.4.178 硬件地址:52:54:4C:98
- PHP编码规范
dcj3sjt126com
编码规范
一、文件格式
1. 对于只含有 php 代码的文件,我们将在文件结尾处忽略掉 "?>" 。这是为了防止多余的空格或者其它字符影响到代码。例如:<?php$foo = 'foo';2. 缩进应该能够反映出代码的逻辑结果,尽量使用四个空格,禁止使用制表符TAB,因为这样能够保证有跨客户端编程器软件的灵活性。例
- linux 脱机管理(nohup)
eksliang
linux nohupnohup
脱机管理 nohup
转载请出自出处:http://eksliang.iteye.com/blog/2166699
nohup可以让你在脱机或者注销系统后,还能够让工作继续进行。他的语法如下
nohup [命令与参数] --在终端机前台工作
nohup [命令与参数] & --在终端机后台工作
但是这个命令需要注意的是,nohup并不支持bash的内置命令,所
- BusinessObjects Enterprise Java SDK
greemranqq
javaBOSAPCrystal Reports
最近项目用到oracle_ADF 从SAP/BO 上调用 水晶报表,资料比较少,我做一个简单的分享,给和我一样的新手 提供更多的便利。
首先,我是尝试用JAVA JSP 去访问的。
官方API:http://devlibrary.businessobjects.com/BusinessObjectsxi/en/en/BOE_SDK/boesdk_ja
- 系统负载剧变下的管控策略
iamzhongyong
高并发
假如目前的系统有100台机器,能够支撑每天1亿的点击量(这个就简单比喻一下),然后系统流量剧变了要,我如何应对,系统有那些策略可以处理,这里总结了一下之前的一些做法。
1、水平扩展
这个最容易理解,加机器,这样的话对于系统刚刚开始的伸缩性设计要求比较高,能够非常灵活的添加机器,来应对流量的变化。
2、系统分组
假如系统服务的业务不同,有优先级高的,有优先级低的,那就让不同的业务调用提前分组
- BitTorrent DHT 协议中文翻译
justjavac
bit
前言
做了一个磁力链接和BT种子的搜索引擎 {Magnet & Torrent},因此把 DHT 协议重新看了一遍。
BEP: 5Title: DHT ProtocolVersion: 3dec52cb3ae103ce22358e3894b31cad47a6f22bLast-Modified: Tue Apr 2 16:51:45 2013 -070
- Ubuntu下Java环境的搭建
macroli
java工作ubuntu
配置命令:
$sudo apt-get install ubuntu-restricted-extras
再运行如下命令:
$sudo apt-get install sun-java6-jdk
待安装完毕后选择默认Java.
$sudo update- alternatives --config java
安装过程提示选择,输入“2”即可,然后按回车键确定。
- js字符串转日期(兼容IE所有版本)
qiaolevip
TODateStringIE
/**
* 字符串转时间(yyyy-MM-dd HH:mm:ss)
* result (分钟)
*/
stringToDate : function(fDate){
var fullDate = fDate.split(" ")[0].split("-");
var fullTime = fDate.split("
- 【数据挖掘学习】关联规则算法Apriori的学习与SQL简单实现购物篮分析
superlxw1234
sql数据挖掘关联规则
关联规则挖掘用于寻找给定数据集中项之间的有趣的关联或相关关系。
关联规则揭示了数据项间的未知的依赖关系,根据所挖掘的关联关系,可以从一个数据对象的信息来推断另一个数据对象的信息。
例如购物篮分析。牛奶 ⇒ 面包 [支持度:3%,置信度:40%] 支持度3%:意味3%顾客同时购买牛奶和面包。 置信度40%:意味购买牛奶的顾客40%也购买面包。 规则的支持度和置信度是两个规则兴
- Spring 5.0 的系统需求,期待你的反馈
wiselyman
spring
Spring 5.0将在2016年发布。Spring5.0将支持JDK 9。
Spring 5.0的特性计划还在工作中,请保持关注,所以作者希望从使用者得到关于Spring 5.0系统需求方面的反馈。