D3D编程必备的数学知识(1)
三维空间中的向量
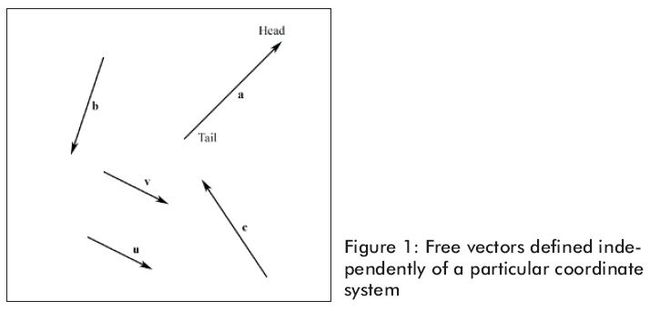
几何学中,我们用有向线段表示向量,如图1。向量的两个属性是他的长度和他的顶点所指的方向。因此,可以用向量来模拟既有大小又有方向的物理模型。例如,以后我们要实现的粒子系统。我们用向量来模拟粒子的速度和加速度。在3D计算机图形学中我们用向量不仅仅模拟方向。例如我们常常想知道光线的照射方向,以及在3D世界中的摄象机。向量为在3维空间中表示方向的提供了方便。
向量与位置无关。有同样长度和方向的两个向量是相等的,即使他们在不同的位置。观察彼此平行的两个向量,例如在图1中u和v是相等的。
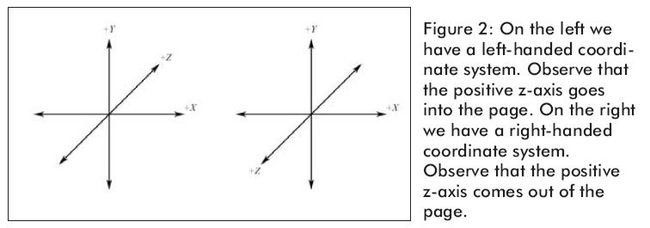
我们继续学习左手坐标系。图2显示的是左手坐标系和右手坐标系。两者不同的是Z轴的方向。在左手坐标系中Z轴是向书的里面去的,而右手坐标系是向书的外边去的。
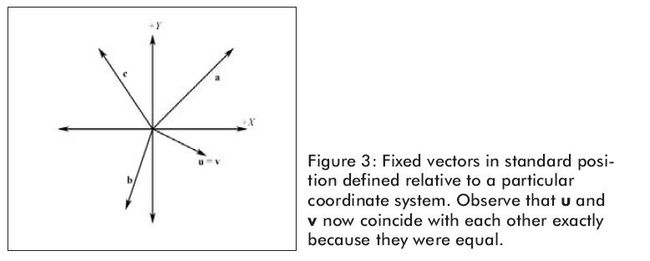
因为向量的位置不能改变它的性质,我们可以把所有向量平移使他们的尾部和坐标系的原点重合。因此,当一个向量在标准位置我们能通过头点来描述向量。图3显示的是图1中的向量在标准位置的样子。
我们通常用小写字母表示一个向量,但有时也用大写字母。如2、3和4维向量分别是:
u = (ux, uy),
N = (Nx, Ny, Nz),
c = (cx, cy, cz, cw)。
我们现在介绍4个特殊的3D向量,就象图4显示的。首先是都由含有0的零向量;它被表示成加粗的0 = (0, 0, 0)。接下来3个特殊的向量标准基向量。它们被叫做i, j和k向量,分别沿着坐标系的x轴,y轴和z轴,并且有1的单位长:i = (1, 0, 0), j = (0, 1, 0), and k = (0, 0, 1)。
注意:只有1个单位长度的向量叫做单位向量(模长为1的向量)。
在D3DX库中,我们能用D3DXVECTOR3类表示3维空间中的向量。它的定义是:
typedef struct D3DXVECTOR3 : public D3DVECTOR {
public:
D3DXVECTOR3() {};
D3DXVECTOR3( CONST FLOAT * );
D3DXVECTOR3( CONST D3DVECTOR& );
D3DXVECTOR3( FLOAT x, FLOAT y, FLOAT z );
// casting
operator FLOAT* ();
operator CONST FLOAT* () const;
// assignment operators
D3DXVECTOR3& operator += ( CONST D3DXVECTOR3& );
D3DXVECTOR3& operator -= ( CONST D3DXVECTOR3& );
D3DXVECTOR3& operator *= ( FLOAT );
D3DXVECTOR3& operator /= ( FLOAT );
// unary operators
D3DXVECTOR3 operator + () const;
D3DXVECTOR3 operator - () const;
// binary operators
D3DXVECTOR3 operator + ( CONST D3DXVECTOR3& ) const;
D3DXVECTOR3 operator - ( CONST D3DXVECTOR3& ) const;
D3DXVECTOR3 operator * ( FLOAT ) const;
D3DXVECTOR3 operator / ( FLOAT ) const;
friend D3DXVECTOR3 operator * ( FLOAT,
CONST struct D3DXVECTOR3& );
BOOL operator == ( CONST D3DXVECTOR3& ) const;
BOOL operator != ( CONST D3DXVECTOR3& ) const;
} D3DXVECTOR3, *LPD3DXVECTOR3;
Note that D3DXVECTOR3 inherits its component data from D3DVECTOR, which is defined as:
typedef struct _D3DVECTOR {
float x;
float y;
float z;
} D3DVECTOR;
向量有它们自己的算法,就象你在D3DXVECTOR3定义中看到的数学运算。现在你不需要知道它们怎么使用。以后介绍这些向量运算以及一些有用的函数和关于向量的,重要的详细资料。
注意:在3D图形程序中,虽然我们主要关心3D向量,但有时也会用到2D和4D向量。在D3DX库中提供了D3DXVECTOR2和D3DXVECTOR4类来分别表现2D和4D向量。不同维数的向量有着和3D向量一样的性质,也就是它们描述大小和方向,仅仅是在不同的维数中。所有这些向量的数学运算对于不同维数向量都有效只是有一个除外,就是向量积。这些运算我们可通过论述3D向量扩展到2D, 4D甚至n维向量。
向量相等
几何学上,有同样方向和长度的两个向量相等。数学上,我们说有同样维数和分量的向量相等。例如:如果ux = vx, uy = vy, 且 uz = vz.那么(ux, uy, uz) = (vx, vy, vz)。在代码中我们能够用“==”判断两个向量相等。
D3DXVECTOR u(1.0f, 0.0f, 1.0f);
D3DXVECTOR v(0.0f, 1.0f, 0.0f);
if( u == v ) return true;
同样的,我们也能用“!=”判断两个向量不相等。
if( u != v ) return true;
注意:当比较浮点数时,必须注意。因为浮点数不是精确的,我们认为相等的两个浮点数是有细微差别的;因此,我们测试它们近似相等。我们定义一个常数EPSILON,把它当作非常小的“buffer”。假如两个数和EPSILON相差很小我们说它们近似相等。换句话说,EPSILON让浮点数有一定的精度。接下来的实例函数是怎样用EPSILON比较两个浮点数相等。
bool Equals(float lhs, float rhs)
{
// if lhs == rhs their difference should be zero
return fabs(lhs - rhs) < EPSILON ? true : false;
}
当我们用D3DXVECTOR3类时不必担心,因为它已经帮我们处理了,但是在一般情况下适当注意比较两个浮点数是很重要的。