| Time Limit: 10000MS | Memory Limit: 65536K | |
| Total Submissions: 25074 | Accepted: 8159 |
Description
Professor Hopper is researching the sexual behavior of a rare species of bugs. He assumes that they feature two different genders and that they only interact with bugs of the opposite gender. In his experiment, individual bugs and their interactions were easy to identify, because numbers were printed on their backs.
Problem
Given a list of bug interactions, decide whether the experiment supports his assumption of two genders with no homosexual bugs or if it contains some bug interactions that falsify it.
Input
Output
Sample Input
2 3 3 1 2 2 3 1 3 4 2 1 2 3 4
Sample Output
Scenario #1: Suspicious bugs found! Scenario #2: No suspicious bugs found!
Hint
题意:
有T个case,每个case开头包含N(1到2000)只虫子和M(1到1000000)个条件关系。每个条件关系都给出a和b,代表a和b可以进行交配,所以属于不同性别,当给出某条关系a和b是同性别的话,说明两只虫子是同性恋。在给出所有关系后,如果有同性恋,则输出Suspicious bugs found!如果没有的话,则输出No suspicious bugs found!
思路:
种类并查集,可以用带权的并查集来做。0代表是同性,1代表的是异性。
AC:
#include<stdio.h>
#define max 2000+5
int root[max],rel[max];
int find(int a)
{
if(root[a]==a) return a;
int r=find(root[a]);
rel[a]=(rel[a]+rel[root[a]])%2;
root[a]=r;
return r;
}
//找根节点且路径压缩
int main()
{
int n;
scanf("%d",&n);
for(int j=1;j<=n;j++)
{
int m,t,temp=0;
scanf("%d%d",&m,&t);
for(int i=1;i<=m;i++)
root[i]=i,rel[i]=0;
//初始化,一开始自结成树,都为同性
while(t--)
{
int a,b;
int fa,fb;
scanf("%d%d",&a,&b);
fa=find(a);
fb=find(b);
if(fa!=fb)
{
root[fa]=fb;
rel[fa]=(rel[b]+1-rel[a]+2)%2;
}
else
{
if((rel[a]-rel[b]+2)%2==0) temp=1;
}
//因为要全部输完才判断是不是同性恋
//所以用temp来标记
}
printf("Scenario #%d:\n",j);
temp?printf("Suspicious bugs found!\n\n"):printf("No suspicious bugs found!\n\n");
}
return 0;
}
递归过程分析:
int find(int a)
{
if(root[a]==a) return a;
int r=find(root[a]);
rel[a]=(rel[a]+rel[root[a]])%2;
root[a]=r;
return r;
}

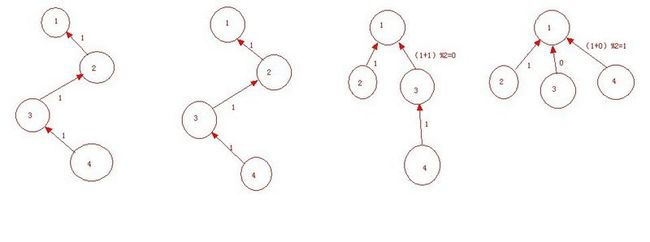
比如找D的根节点,那么就会执行find(D)->find(C)->find(B)->find(A)(图1),找到根节点A后,r变量就会存储A这个节点。这时候就会返回根节点A到find(B)函数的r中,这时候开始路径压缩,根据公式rel[a]=(rel[a]+rel[root[a]]),,那么B路径压缩后的权值就是B本身的权值加上B根节点的权值(B根节点为A)(图2),就是1+0=0,更改权值后,将B的根节点更改为A,返回A节点到find(C)的r中。
这时候到find(C)函数,C路径压缩后的权值就是C本身的权值加上C根节点的权值(C根节点为B),所以就是1+2=3,更改权值后,将C的根节点从B更改成A,返回A节点到find(B)的r中,以此类推……
总结全部过程就是D->C->B->A然后A->B->C->D,因为权值一直在累加,所以只要一直加上上一层的权值即可。所以这两句话的顺序不可调转,如果调转的话,就是先改变根节点,再改变权值。更改根节点后,rel[root[a]]则一直等于0,那么最后更改得出来的权值一直只是本身的权值加上0,就相当于没有改变权值,只是单纯把根节点改变而已。
rel[a]=(rel[a]+rel[root[a]])%2; root[a]=r;
上面的递归过程是普遍例子,如果对应上本题的话,公式就是rel[a]=(rel[a]+rel[root[a]])%2,如图,然后通过图就可以看出,1和2是异性,1和3是同性,1和4是异性了。
总结:
注意输出格式,要空出一行。