小波图像重构 Matlab 程序 - V2.0版
注意!程序有新的修正了,详细请见如下文章:
%----------------------------------------------------------%
小波分解重构 V2.0 版程序存在的问题分析
小波图像分解 Matlab 程序 - V3.0版
小波图像重构 Matlab 程序 - V3.0版
%----------------------------------------------------------%
本文给出相应的小波图像重构程序的修正版代码,图像分解程序的代码请见下文:
《小波图像分解
Matlab
程序
- V2.0
版
》
下面给出重构程序的代码,包括有:
mywaverec2(), myidwt2(), myidwt(), upspl()
。
function xrec=mywaverec2(coef,recdim,wname)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
函数
MYWAVEREC2()
对输入的分解系数矩阵
x
进行
recdim
层重构,得到重构矩阵
xrec
%
输入参数:
y ——
分解系数矩阵;
% recdim ——
重构级数;
% wname ——
重构所用的小波函数
%
输出参数:
xrec ——
重构矩阵。
% % Copyright by Zou Yuhua ( chenyusiyuan ), original : 2007-11-10, modified: 2008-06-04
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
求小波函数对应的重构滤波器组系数
[Lo_R,Hi_R] = wfilters(wname,'r');
%
通过小波系数矩阵求出图像的分解级数
decdim
[yr,yc]=size(coef);
%
小波系数矩阵
coef
是一个细胞矩阵(
cell matrix
)
,
其中有
yr
个子矩阵,
yc=1
decdim=(yr-1)/3;
%
图像的
N
级分解会产生
1
个低频矩阵,
N*3
个高频矩阵
if decdim<recdim
error(['Reconstruction level can not larger than decomposition level ( declev = ',num2str(decdim),' )'])
end
rcA=coef{1};
for i=1:recdim
%
依次获取第
decdim
级至第(
decdim - recdim + 1
)级的高频系数矩阵
rcV=coef{(i-1)*3+2};
rcH=coef{(i-1)*3+3};
rcD=coef{(i-1)*3+4};
rcA=myidwt2(rcA,rcV,rcH,rcD,Lo_R,Hi_R);
%
第
N
级重构得到第
N-1
级低频系数矩阵
end
xrec=rcA;
%
重构结束后得到的矩阵
rcA
即为输出矩阵
xrec
figure;
xr=uint8(xrec);
%
将矩阵
xrec
的数据格式转换为适合显示图像的
uint8
格式
[sr,sc]=size(xr);
imshow(xr);
title(['Reconstructed Image. DecLevel = ',num2str(decdim),' , RecLevel = ',num2str(recdim)]);
xlabel(['Size : ',num2str(sr),'*',num2str(sc)]);
%
显示重构矩阵的大小
function outcA=myidwt2(rcA,rcV,rcH,rcD,Lo_R,Hi_R)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
函数
MYIDWT2()
对输入的子矩阵序列进行逆小波变换,重构出矩阵
y
%
输入参数:
rcA,rcV,rcH,rcD ——
第
N
级低频、高频系数矩阵
% Lo_R,Hi_R ——
图像重构用到的低通、高通滤波器系数
%
输出参数:
outcA ——
第
N-1
级低频系数矩阵,当
N-1=0
时即为重构图像。
% Copyright by Zou Yuhua ( chenyusiyuan ), original : 2007-11-10, modified: 2008-06-04
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
系数矩阵规范化,使各矩阵大小一致
[m,n]=size(rcA);
rcV=rcV(1:m,1:n);
rcH=rcH(1:m,1:n);
rcD=rcD(1:m,1:n);
%
将四个第
N
级系数矩阵组合成一个矩阵
tmp_mat=[rcA,rcV;rcH,rcD];
[row,col]=size(tmp_mat);
%
这里
tmp_mat
的行列数比第
N-1
级低频矩阵
cA(N-1)
的要长
lnf-1
行(列)
%
求出滤波器的长度
lnf=length(Lo_R);
for k=1:col
%
首先对组合矩阵
tmp_mat
的每一列,分开成上下两半
ca1=tmp_mat(1:row/2,k);
%
分开的两部分分别作为平均系数序列
ca1
、细节系数序列
cd1
cd1=tmp_mat(row/2+1:row,k);
% ca1
、
cd1
的长度恰好等于
tmp_mat
的行数
row
tmp1=myidwt(ca1,cd1,Lo_R,Hi_R);
%
重构序列的长度是(
row+lnf-1
)
%
注意不论是分解或重构,卷积后序列的长度都会比原序列要长
(
lnf-1
)
%
所以这里
tmp1
的长度要比
cA(N-1)
的行数长
2*(lnf-1
)行
%
故有效的重构序列应该是以
tmp1
中心的长度为(
row-lnf+1
)的那一段
%
通过
Matlab
函数
wkeep()
来实现截取
yt1(:,k)=wkeep(tmp1,row-lnf+1);
%
截取后的重构序列存入缓存矩阵
yt1
end
[row1,col1]=size(yt1);
for j=1:row1
%
将缓存矩阵
yt1
的每一行,分开成左右两半
ca2=yt1(j,1:col1/2);
%
分开的两部分分别作为平均系数序列
ca2
、细节系数序列
cd2
cd2=yt1(j,col1/2+1:col1);
tmp2=myidwt(ca2,cd2,Lo_R,Hi_R);
outcA(j,:)=wkeep(tmp2,col-lnf+1);
%
同理,也要截取
tmp2
中间长度为(
col-lnf+1
)的那一段,存入输出矩阵
outcA
end
function y = myidwt(cA,cD,lpr,hpr);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
函数
MYIDWT()
对输入的小波分解系数进行逆离散小波变换,重构出信号序列
y
%
输入参数:
cA ——
平均部分的小波分解系数;
% cD ——
细节部分的小波分解系数;
% lpr
、
hpr ——
重构所用的低通、高通滤波器。
% Copyright by Zou Yuhua ( chenyusiyuan ), original : 2007-11-10
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
lca=length(cA);
%
求出平均、细节部分分解系数的长度
lcd=length(cD);
while (lcd)>=(lca)
%
每一层重构中,
cA
和
cD
的长度要相等,故每层重构后,
%
若
lcd
小于
lca
,则重构停止,这时的
cA
即为重构信号序列
y
。
upl=upspl(cA);
%
对平均部分系数进行上抽样
cvl=conv(upl,lpr);
%
低通卷积
cD_up=cD(lcd-lca+1:lcd);
%
取出本层重构所需的细节部分系数,长度与本层平均部分系数的长度相等
uph=upspl(cD_up);
%
对细节部分系数进行上抽样
cvh=conv(uph,hpr);
%
高通卷积
cA=cvl+cvh;
%
用本层重构的序列更新
cA
,以进行下一层重构
cD=cD(1:lcd-lca);
%
舍弃本层重构用到的细节部分系数,更新
cD
lca=length(cA);
%
求出下一层重构所用的平均、细节部分系数的长度
lcd=length(cD);
end
% lcd < lca
,重构完成,结束循环
y=cA;
%
输出的重构序列
y
等于重构完成后的平均部分系数序列
cA
function y=upspl(x);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
函数
Y = UPSPL(X)
对输入的一维序列
x
进行上抽样,即对序列
x
每个元素之间
%
插零,例如
x=[x1,x2,x3,x4],
上抽样后为
y=[x1,0,x2,0,x3,0,x4]; %
% Copyright by Zou Yuhua ( chenyusiyuan ), original : 2007-11-10
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
N=length(x);
%
读取输入序列长度
M=2*N-1;
%
输出序列的长度是输入序列长度的
2
倍再减一
for i=1:M
%
输出序列的偶数位为
0
,奇数位按次序等于相应位置的输入序列元素
if mod(i,2)
y(i)=x((i+1)/2);
else
y(i)=0;
end
end
运行结果图示:
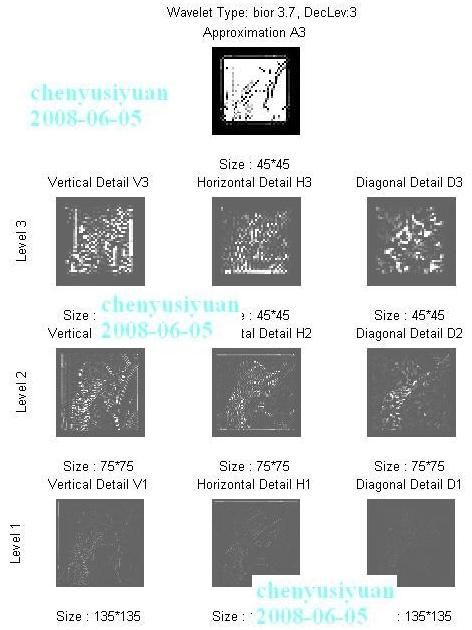
1、Bior3.7 小波 3 级分解
由分解图可见,低频系数图像的边缘是有一定宽度的黑色边带,这是由于行、列变换时卷积产生的冗余数据,黑色表示这些数据的值为零,边带宽度与滤波器长度有关。图像原始大小为 256*256,n = 256, bior3.7小波的滤波器长度为 lnf=16,则上图中各级系数矩阵的大小可由公式 lenca1 = floor((n-1)/2)+lnf 计算得出:
Level-1: 256+16-1=271, floor(271/2)= 135 (128) ( 7)
Level-2: 135+16-1=150, floor(150/2)= 75 ( 64) (11)
Level-3: 75+16-1= 90, floor( 90/2)= 45 ( 32) (13)
上面两列括号内的数据,第1列是有效的图像小波分解系数大小,第2列是黑色边带的宽度。
2、Bior3.7 小波 1 级重构
3、Bior3.7 小波 2 级重构
4、Bior3.7 小波 3 级重构
5、最后做一个有趣的实验,如果将分解后得到的平均系数 cA 清零,保留其它细节系数,然后进行重构,我们就会得到下面这样的重构图像:
这个重构图像完全是由各级细节系数重构得到的,可以说它表现了原始图像的轮廓、边缘特征的所有信息。应该可以作为图像纹理分析、边缘检测等应用的基础,呵呵,不知说的是否恰当,希望能抛砖引玉,欢迎大家拍砖,多多讨论交流!