| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 26079 | Accepted: 7872 |
Description
Assume N (N <= 10^5) criminals are currently in Tadu City, numbered from 1 to N. And of course, at least one of them belongs to Gang Dragon, and the same for Gang Snake. You will be given M (M <= 10^5) messages in sequence, which are in the following two kinds:
1. D [a] [b]
where [a] and [b] are the numbers of two criminals, and they belong to different gangs.
2. A [a] [b]
where [a] and [b] are the numbers of two criminals. This requires you to decide whether a and b belong to a same gang.
Input
Output
Sample Input
1 5 5 A 1 2 D 1 2 A 1 2 D 2 4 A 1 4
Sample Output
Not sure yet. In different gangs. In the same gang.
题意:
有T(1到20)个case,每个case开头包含N(1到100000)个人和M(1到100000)条信息。A[x][y]表示要询问x和y是什么关系,关系一共有三种:不能确定,是同伙,是敌人;D[x][y]表示x和y属于不同的团伙。
思路:
首先要弄清楚3种关系到底是怎样的,同伙和敌人很容易理解,但是为什么会有不能确定的关系呢?比如有5个人,1和2是同伙关系,2和3是敌人关系,那么1和3很自然的也是敌人关系了,那么1和4呢?就是不能确定的关系了。说明当集合很多的时候,在没有给出确定关系之前,所有与之未确定的人配对都是不确定关系的。
之前做的都是简单的并查集,直接判断在不在一个集合就行了。可是现在关系有3种,如果还用原来的方法肯定是不行的。所以每当确定一个关系就合并到一个集合中,同时每个元素的权值代表不同的意义,0代表是同伙,1代表是敌人。如果不在一个根节点上的话,就说明关系未确定,属于未确定关系。
这时候的并查集就加上了权值了,权值代表的是与父亲节点的关系,说明父亲节点改变的话,该节点的权值也会发生相应的变化,这时候就要两个方面:路径压缩和合并,因为两者都有父亲节点的变化,说明权值要发生相应的变化。这些变化可以用向量的加减来表示,用root存储每个节点的根节点,用re表示从该节点出发的向量权值,比如:
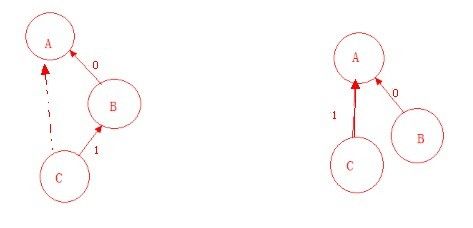
1.压缩的时候:
比如将C节点连到A的时候,那么就会有条从C到A的向量,那么C到A这条向量的权值就是1+0=1,所以说明B和A是同伙,B和C是敌人,那么则推出A和C是敌人,对应的代码就是re[a]=(re[a]+re[root[a]])%2,%2是为了保证当相加超过2时的情况,这样取出来的结果能保证是0或者1。
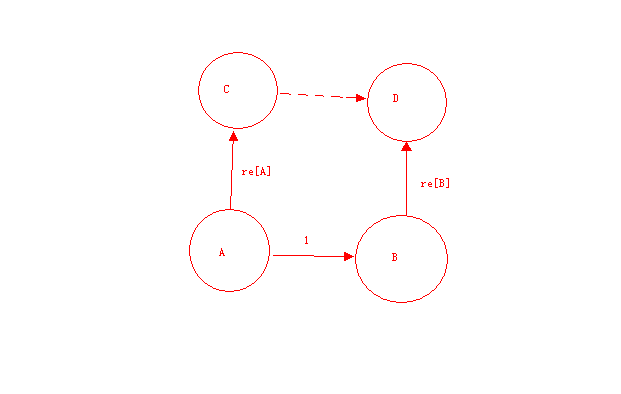
2.合并的时候:
当知道A和B是敌人,则A和B之间有条权值为1的边,C和D分别是A和B的根节点,所以要把合并C到D,那么C到D之间的权值就是-re[A]+1+re[B]了;如果是把D合到C则公式是re[A]-1-re[B]了。同时,如果同样为了保证只取到0和1两个值,可以进行+2在%2处理。所以公式为(-re[A]+1+re[B]+2)%2或者(re[A]-1-re[B]+2)%2。这样的话,也可以知道c和d之间的关系了。
3.查询:
当知道两个元素处于同一根节点之后判断是同伙还是敌人,则公式为(re[D]-re[C]+2)%2。如果值为0,说明为同伙,如果是1,说明为敌人。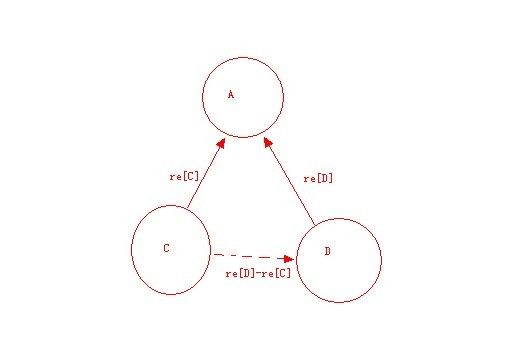
AC:
#include<stdio.h>
#define max 100000+5
int root[max],re[max];
int find(int a)
{
if(root[a]==a) return a;
int r=find(root[a]);
re[a]=(re[a]+re[root[a]])%2;
return root[a]=r;
}
//这里的递归写法有点难理解
//先从最低下往上找到根节点
//通过不断返回根节点来进行路径压缩,压缩顺序为根节点往下压缩
//那么权值就为该层权值加上上一层权值
//return root[a]=r相当于root[a]=r;return r;
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int m,t;
scanf("%d%d",&m,&t);
for(int i=1;i<=m;i++)
root[i]=i,re[i]=0;
while(t--)
{
char c;
int a,b,fa,fb;
scanf(" %c%d%d",&c,&a,&b);
fa=find(a);
fb=find(b);
if(c=='A')
{
if(fa==fb)
{
if((re[a]-re[b]+2)%2==0) printf("In the same gang.\n");
else printf("In different gangs.\n");
}
else printf("Not sure yet.\n");
}
else
{
if(fa!=fb)
{
root[fa]=fb;
re[fa]=(-re[a]+re[b]+1+2)%2;
//这里可以把fa并到fb,也可以把fb并到fa,两者的公式不一样
}
}
}
}
return 0;
}
总结:
1.带权并查集相当于在树的边上加上了信息,与之前的做法会有所不同;
2.递归的理解有点难理解,顺序有点难搞清,想模拟也不知道如何模拟;
3.fa并到fb与fb并到fa公式是不一样的,但是结果是一样的;
4.巧用向量来理解。