模拟退火

引用：http://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html

 

 

一. 爬山算法 ( Hill Climbing )
         介绍模拟退火前，先介绍爬山算法。爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。

         爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。如图1所示：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。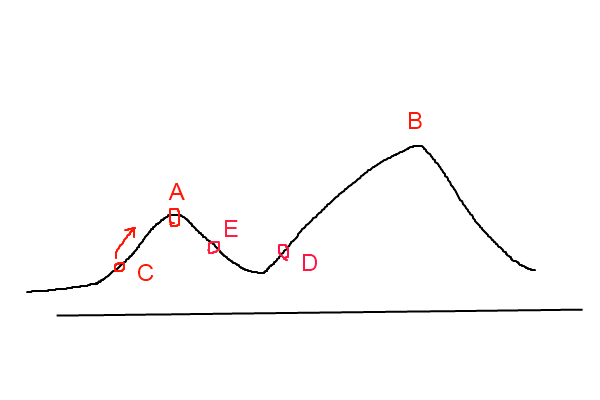

二. 模拟退火(SA,Simulated Annealing)思想
         爬山法是完完全全的贪心法，每次都鼠目寸光的选择一个当前最优解，因此只能搜索到局部的最优值。模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以图1为例，模拟退火算法在搜索到局部最优解A后，会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点，于是就跳出了局部最大值A。
         模拟退火算法描述：
         若J( Y(i+1) )>= J( Y(i) )  (即移动后得到更优解)，则总是接受该移动
         若J( Y(i+1) )< J( Y(i) )  (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）

　　这里的“一定的概率”的计算参考了金属冶炼的退火过程，这也是模拟退火算法名称的由来。
　　根据热力学的原理，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：
　　　　P(dE) = exp( dE/(kT) )
　　其中k是一个常数，exp表示自然指数，且dE<0。这条公式说白了就是：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于dE总是小于0（否则就不叫退火了），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。
　　随着温度T的降低，P(dE)会逐渐降低。
　　我们将一次向较差解的移动看做一次温度跳变过程，我们以概率P(dE)来接受这样的移动。

　　关于爬山算法与模拟退火，有一个有趣的比喻：
　　爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。
　　模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。

下面给出模拟退火的伪代码表示

/*
 *  J(y)：在状态y时的评价函数值
 *  Y(i)：表示当前状态
 *  Y(i+1)：表示新的状态
 *  r： 用于控制降温的快慢（0<r<1，越小降温越快）
 *  T： 系统的温度，系统初始应该要处于一个高温的状态
 *  T_min ：温度的下限，若温度T达到T_min，则停止搜索
*/
while( T > T_min )
{
　　dE = J( Y(i+1) ) - J( Y(i) ) ;  

　　if ( dE >= 0 )  //表达移动后得到更优解，则总是接受移动
        Y(i+1) = Y(i) ;  //接受从Y(i)到Y(i+1)的移动
　　else
　　{
    // 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也
        if ( exp( dE/T ) > random( 0 , 1 ) )
            Y(i+1) = Y(i) ;  //接受从Y(i)到Y(i+1)的移动
　　}
　　T = r * T ;  //降温退火 ，0<r<1 。r越大，降温越慢；r越小，降温越快
　　/*
　　* 若r过大，则搜索到全局最优解的可能会较高，但搜索的过程也就较长。若r过小，则搜索的过程会很快，但最终可能会达到一个局部最优值
　　*/
　　i ++ ;
}

 

三. 使用模拟退火算法解决旅行商问题 (TSP)

　　旅行商问题 ( TSP , Traveling Salesman Problem ) ：有N个城市，要求从其中某个问题出发，唯一遍历所有城市，再回到出发的城市，求最短的路线。
　　旅行商问题属于所谓的NP完全问题，精确的解决TSP只能通过穷举所有的路径组合，其时间复杂度是O(N!) 。
　　使用模拟退火算法可以比较快的求出TSP的一条近似最优路径。（使用遗传算法也是可以的，我将在下一篇文章中介绍）模拟退火解决TSP的思路：

1. 产生一条新的遍历路径P(i+1)，计算路径P(i+1)的长度L( P(i+1) )
2. 若L(P(i+1)) < L(P(i))，则接受P(i+1)为新的路径，否则以模拟退火的那个概率接受P(i+1) ，然后降温
3. 重复步骤1，2直到满足退出条件

　　产生新的遍历路径的方法有很多，下面列举其中3种：
1. 随机选择2个节点，交换路径中的这2个节点的顺序。
2. 随机选择2个节点，将路径中这2个节点间的节点顺序逆转。
3. 随机选择3个节点m，n，k，然后将节点m与n间的节点移位到节点k后面。

 

    这个实现参考了这里：   http://www.codeproject.com/Articles/26758/Simulated-Annealing-Solving-the-Travelling-Salesma

        原始代码采用c#实现，我用C++重写了一遍。但不知为何(???)

 

   模拟退火代码有3个关键点，引用以上原文中的描述：

1. Configuration setting : This is the permutation of the cities from 1 to N, given in all orders. Selecting an optimal one between these permutations is our aim.
2. Rearrangement strategy : The strategy that we will follow here is replacing sections of the path, and replacing them with random ones to retest if this modified one is optimal or not.
3. The objective function (which is the aim of the minimization): This is the sum of the distances between all the cities for a specific order.

 

TSP求解代码

/*
	模拟退火(simulated annealing)求解TSP, C++实现
*/
#include <iostream>
#include <fstream>
#include <sstream>
#include <vector>
#include <cstdlib>
#include <string>
#include <cmath>
using namespace std;

const int MAX_LINE_LENGTH=1000;
const int MAX=100;

double map[MAX][MAX];

vector<int> curOrder;
vector<int> nextOrder;

double shortestDist=1<<29;
double temperature=10000.0;
double deltaDist=0;
double coolingRate=0.9999;
double absoluteTemperature=0.00001;

//当前TSP路线的长度
double getDist(vector<int> order){
	double dist=0;

	for(int i=0;i<=order.size()-2;i++){
		dist+=map[order[i]][order[i+1]];
	}

	if(order.size()>1){
		dist+=map[order[order.size()-1]][order[0]];
	}

	return dist;
}

//状态转移：交换当前TSP回路上的任意两个点，范围[0, order.size-1]
vector<int> getNextState(vector<int> order){
	vector<int> newOrder;
	for(int i=0;i<order.size();i++){
		newOrder.push_back(order[i]);
	}

	int i=rand()%order.size();	//rand()产生0~RAND_MAX间任意数，需要引入<cstdlib>，即使原来的<stdlib.h>
	int j=rand()%order.size();
	int tmp=newOrder[i];
	newOrder[i]=newOrder[j];
	newOrder[j]=tmp;

	return newOrder;
}


int main(){
	//1. 读取地图
	ifstream  in("..\\TSP\\Cities.txt");

	char line[MAX_LINE_LENGTH];
	int line_no=0;

	while(in.getline(line,MAX_LINE_LENGTH)){	//C++: 按行读取文件

		//C++: char[] / string 的split操作
		string str_line(line);
		stringstream ss(str_line);

		string buf;
		int col_no=0;
		while(ss>>buf){
			double f=atof(buf.data());	//C++: char*转...  (analogy to atoi() )
			map[line_no][col_no]=f;

			col_no++;
		}
		
		line_no++;
	}

	//2. 模拟退火求解TSP

	//init configuration(state)
	for(int i=0;i<line_no;i++){
		curOrder.push_back(i);
	}

	int iteration=0;
	//simulated annealing
	while(temperature>absoluteTemperature){
		nextOrder=getNextState(curOrder);

		deltaDist=getDist(nextOrder)-shortestDist;

		if( deltaDist<0 || exp(-deltaDist/temperature)> (rand()/double(RAND_MAX)) ){	//C++: 产生随机数double∈[0,1]
			for(int i=0;i<nextOrder.size();i++){
				curOrder[i]=nextOrder[i];
			}

			shortestDist=shortestDist+deltaDist;
		}

		temperature*=coolingRate;
		iteration++;
	}

	cout<<iteration<<endl;

	cout<<"shortest distance is "<<shortestDist<<endl;
	cout<<"the order is: ";
	for(int i=0;i<curOrder.size();i++){
		cout<<curOrder[i]<<"\t";
	}

	return 0;
}

 

测试数据Cities.txt

0.0 5.0 5.0 6.0 7.0 2.0 5.0 2.0 1.0 5.0 5.0 1.0 2.0 7.1 5.0
5.0 0.0 5.0 5.0 5.0 2.0 5.0 1.0 5.0 6.0 6.0 6.0 6.0 1.0 7.1
5.0 5.0 0.0 6.0 1.0 6.0 5.0 5.0 1.0 6.0 5.0 7.0 1.0 5.0 6.0
6.0 5.0 6.0 0.0 5.0 2.0 1.0 6.0 5.0 6.0 2.0 1.0 2.0 1.0 5.0
7.0 5.0 1.0 5.0 0.0 7.0 1.0 1.0 2.0 1.0 5.0 6.0 2.0 2.0 5.0
2.0 2.0 6.0 2.0 7.0 0.0 5.0 5.0 6.0 5.0 2.0 5.0 1.0 2.0 5.0
5.0 5.0 5.0 1.0 1.0 5.0 0.0 2.0 6.0 1.0 5.0 7.0 5.0 1.0 6.0
2.0 1.0 5.0 6.0 1.0 5.0 2.0 0.0 7.0 6.0 2.0 1.0 1.0 5.0 2.0
1.0 5.0 1.0 5.0 2.0 6.0 6.0 7.0 0.0 5.0 5.0 5.0 1.0 6.0 6.0
5.0 6.0 6.0 6.0 1.0 5.0 1.0 6.0 5.0 0.0 7.0 1.0 2.0 5.0 2.0
5.0 6.0 5.0 2.0 5.0 2.0 5.0 2.0 5.0 7.0 0.0 2.0 1.0 2.0 1.0
1.0 6.0 7.0 1.0 6.0 5.0 7.0 1.0 5.0 1.0 2.0 0.0 5.0 6.0 5.0
2.0 6.0 1.0 2.0 2.0 1.0 5.0 1.0 1.0 2.0 1.0 5.0 0.0 7.0 6.0
7.0 1.0 5.0 1.0 2.0 2.0 1.0 5.0 6.0 5.0 2.0 6.0 7.0 0.0 5.0
5.0 7.0 6.0 5.0 5.0 5.0 6.0 2.0 6.0 2.0 1.0 5.0 6.0 5.0 0.0

 

四. POJ例题

 

POJ 1379 Run Away

解题思路：

      其实看程序就比较好理解启发式算法的思想了，但是我找了很多解题报告，发现都没有出现概率性选择并不是最优解的解决办法，有的利用了同时产生好几个点，利 用并发性，这也不能算是概率性选择，还是搞不太明白怎么办。但是就这道题说还是比较简单的，确定步长，减小速度为0.9，因为精度比较低，所以就比较好办 了。保存一个当前最优解集，利用随机性，步长和最优解集产生新的最优解集，最后得到的解有很大程度上不是最优解，但是对于这道题这个精度来说还是可以做到的。

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<string>
 #include<ctime>
 #include<cstdlib>
 using namespace std;
 
 const int NUM=20;
 const int RAD=1000;
 
 struct point
 {
     double x,y,val;
     point(){}
     point(double _x,double _y)
     {
         x=_x;
         y=_y;
     }
 };
 point p[10001],May[NUM],e1,e2;
 int n;
 double X,Y;
 
 double dis(point a,point b)
 {
     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
 }
 double judge(point t)//评价函数，得到点t的评价值val
 {
     double len=dis(t,p[0]);
     for(int i=1;i<n;i++)
     len=min(len,dis(t,p[i]));
     return len;
 }
 double Rand(){return rand()%(RAD+1)/(1.0*RAD);}//随机产生0-1的浮点数
 point Rand_point(point a,point b)//在a,b框定的四边形内随机生成点
 {
     double xx=a.x+(b.x-a.x)*Rand();
     double  yy=a.y+(b.y-a.y)*Rand();
     point tmp=point(xx,yy);
     tmp.val=judge(tmp);
     return tmp;
 }
 void solve(double D)
 {
     May[0]=point(0,0);
     May[1]=point(X,Y);
     May[2]=point(0,Y);
     May[3]=point(X,0);
     May[0].val=judge(May[0]);
     May[1].val=judge(May[1]);
     May[2].val=judge(May[2]);
     May[3].val=judge(May[3]);    
     
     //4个顶点的可能行较大，所以特殊构造
     for(int i=4;i<NUM;i++)
             May[i]=Rand_point(May[0],May[1]);//步骤2
     
     int iteration=0;
     while(D>0.01)//步骤 3
     {
         for(int i=0;i<NUM;i++)
         for(int j=0;j<NUM;j++)
         {
             point tmp=Rand_point(    point(max(0.0,May[i].x-D),max(0.0,May[i].y-D)),
                                      point(min(X,May[i].x+D),min(Y,May[i].y+D))
                                 );
             if(tmp.val>May[i].val)
             {
                 May[i]=tmp;
             }
         }
         D*=0.9;
         iteration++;
     }
     
     //cout<<"iteration="<<iteration<<endl;
     point ans;
     ans.val=0;
     for(int i=0;i<NUM;i++){
         //cout<<"("<<May[i].x<<", "<<May[i].y<<") val="<<May[i].val<<endl;
         if(May[i].val>ans.val)
             ans=May[i];
     }
     printf("The safest point is (%.1f, %.1f).\n",ans.x,ans.y);
 }
 int main()
 {
     srand(time(0));
     e2=point(0,0);
     int Case;
     int i;
     scanf("%d",&Case);
     while(Case--)
     {
         scanf("%lf%lf%d",&X,&Y,&n);
         for(i=0;i<n;i++)
         {
             scanf("%lf%lf",&p[i].x,&p[i].y);
         }
         solve(max(Y,X));
     }
     system("pause");
     return 0;
 }

五. 算法评价
        模拟退火算法是一种随机算法，并不一定能找到全局的最优解，可以比较快的找到问题的近似最优解。 如果参数设置得当，模拟退火算法搜索效率比穷举法要高。