资源受限的数据流处理优化算法的发现之旅

资源受限的数据流处理优化算法的发现之旅

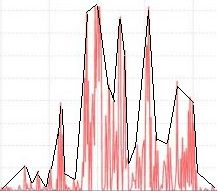
前言：本文的内容源自我最近作的一个胎心检测仪的项目，该项目所使用的平台是一个基于MP430的嵌入式系统，CPU频率12M（超频后），系统内存为10k，采样率为600个数据（整数）/秒。我的职责是处理如下图所示的心律数据流，找出在下图所示的一维数据流中有多少个波峰（即心跳次数）。本以为是个分分钟就能搞定的简单问题（不知你看到这里是不是和我有同感 J），没想到后来越做越复杂，越做越困难重重；很多时候本以为希望就在眼前，却一次又一次的失望。在试过n种方法之后，虽然问题勉强解决了，但实际结果仍然不甚完美。所以希望借助本文来找到一些对此感兴趣的朋友的批评指正，更希望得到一些算法上的建设性意见，来帮助我最终彻底解决这个问题。

<shapetype id="_x0000_t75" stroked="f" filled="f" path="m@4@5l@4@11@9@11@9@5xe" o:preferrelative="t" o:spt="75" coordsize="21600,21600"></shapetype> 1 主要问题描述

我们的目标很简单，就是要确定能够上图所示的心律数据中有多少个波形（波峰数或波谷数）。我们所获得的数据就是一组整数，范围是0-4000，我们将采集后的数据放到了一个数组中（该数组用 S表示）。注意到我们的内存只有10K；采样率600个数据（整数）/秒（这个采样率不能再降了，否则将会影响处理器的运算速度）；我们的项目要求胎心率的显示范围为30-240次/分钟。上图所示即为达到最高显示范围的人造数据。然而我们一次可以处理的数据并不能太多，因为每一个数据都需要一个2字节int来保存，于是1500个数据就需要占用3k内存，更何况如果我们采用傅立叶变换，每一个数据需要用一个4字节的double或float来保存，还要除去系统其他程序占用的空间，所以留给我们空间实在非常有限。晶阵频率为12M的处理器的速度有多快？和我们在PC机上运行程序相差多远呢？这些问题我将在后面的内容中给出我们的试验实例供各位参考。所以，这个问题的要求就很是苛刻—算法既要简单，又要节省空间。怎么样，开始头痛了是不是？

2 滤波之旅

对于这个问题，我首先想到的方法不是滤波，而是希望通过更简单的方法解决问题。我的基本想法是设法找出波形与波形之间的间隙，例如设定一个经验阈值V，低于这个阈值的数据认为是0。通过扫描S（保存数据的数组），如果我们能找到连续P（P为某个经验值）个低于阈值V的数据，则认为找到了波谷，从而找到了波谷数。关键问题是两个经验值V和P都不容易找到，即并没有任何理论依据告诉我们到底应该怎样取值，就算我们采用真正的胎动数据来做试验以获得这两个经验值，但我们很难找到心律不正常的（即超出正常心率范围的数据）数据样本来进行验证，因为没有任何证据表明在正常情况下和在异常情况下的这两个经验值满足简单的线形关系。更糟糕的是处于谷底的数据时不时可能就会“蹦”出一个超过阈值的数据来干扰我们查找谷底的工作。于是我们打算采用一些滤波的方法解决问题。

我的目标是减少毛刺，取得图形的包络线。事实证明，我这回的想法仍然很幼稚。我先用包括中值滤波、开运算、闭运算 *进行预处理，然后再用一次或二次插值再行处理，在最好的结果下只能得到如下图所示的包络线。显然这个结果不能帮助我们解决问题，于是我的思路就转向更为复杂的、专门用于对信号进行消噪的处理方法上。

*注:任何一本图像处理书中都会有的最最基本的图像处理方法。

3 消噪之旅

在简单滤波的方法失败之后，我首先想到的是既然这是一种信号的波形，而一个干净的信号的波形应该是连续且平滑的，但我们的波形却又很多缺口和毛刺。这显然是原始信号与噪声信号叠加之后产生的结果，那我能不能用消除噪声的方法来处理这些数据呢？那我就动手来试试看！

l 小波分解算法

我首先想到的不是去图书馆翻信号处理的书，而是求教于数学计算和信号处理的大拿--Matlab的帮助文档。通过努力的查找，我终于找到了一种适用于本文问题的方法—小波分解消噪算法。鉴于小波分析理论市场复杂且有众多数学推理，我们只大概了解什么是小波分析及其消噪原理就可以了。简单来说，小波分析是近几十年才兴起的新的数学分析方法。它把数据、函数或算子分割成不同频率的成分，然后再用分解的方法去研究对应尺度下的成分。小波分解消噪法的原理是将原始信号分解为两部分，即高频部分和低频部分，其中高频部分就是噪声。于是只要我们递归地进行多次分解，同时去掉高频噪声部分。在利用小波分解的可逆性，将去掉噪声之后的信号还原，就可以得到足够平滑的信号曲线。通过在Matlab7上进行5层分解消噪，我们就能获得给常平滑的曲线。实现中，我采用Daubechies小波作为小波基，进行6层分解所得到的结果如下

从图上来看，经过处理之后结果与原始图像的波峰数基本一致，前景一片光明啊！但是在随后的程序实现中我发现，由于要进行多层分解，并且最后还要进行逆运算以恢复到去噪后的原始波形，所以要保留中间数据，即要将分解后的数据保存在另外的存储空间中。这个要求是非常致命的，假设我们一次处理1000个整形数据，即需要大约2K的存储空间，5层分解共需12K（包括原始数据）。这已经朝过了我们10K的总存储量。于是我慨叹：现在台式机标配都1G内存了，可怜我只有10K内存可用，惨不忍睹啊！！

l 平均频移自相关算法

平均频移自相关算法是我在网上找到的一篇专门处理此类问题的论文，我如获至宝。文章提出的信号处理方法--平均频移自相关方法的主要处理方法是：先在移动的时间间隔内对信号进行傅立叶变换，得到信号的时频分布，然后求对应的每个频谱的平均频率得到多谱勒信号的平均频率曲线，最后利用自相关算法从平均频率曲线中提取胎儿心脏跳动曲线。通过模拟仿真和实际信号处理，证明该方法能准确地从超声多谱勒信号中提取胎心率信号。

所以该算法的第一步骤是傅利叶变换取其频谱：

第二步是定义平均频率：

最后一步自定义如下所示：

在实验中，我采用了如下参数设定：

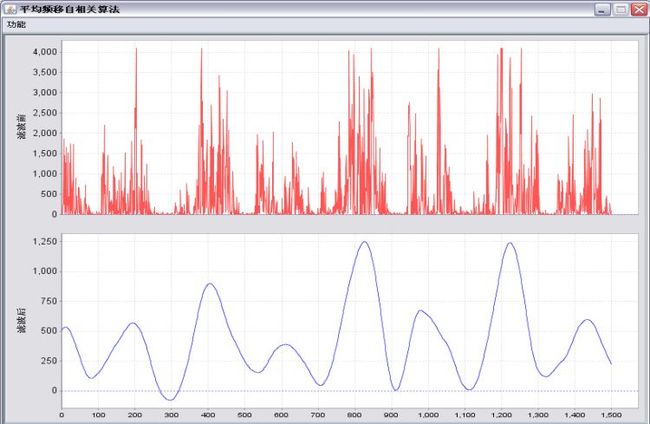
具体的实验结果如下图所示：

乍一看，结果还不错嘛，基本上和原始信号相一致。不过仔细分析过后，发现了若干非常致命的问题。

问题一：这种算法需要用一段信号作为模板，来作为它进行自相关操作的依据。而根据算法所给出的公式，经过子相关之后剩余的信号的长度只能是“原始长度-模板长度”，而模板通常是一个波形，于是我们平白无故的就损失了一个波形，严重浪费了空间利用率。同时，我们的模板不能乱取，最好是取得一个波形，这样才能计算出“体态良好”的波形，否则波形就会严重失真，这意味着模板的选取对最后的结果有着决定性的影响。这不是耍我吗？我要是知道怎么取出一个波形还用这么麻烦？！所以在取得模板的时候只能采用最开始提到的控制阈值的方法来大概找到一个波形的开始部分。这样的解决方法实在是无奈之举，论文里也没提怎么处理，且人家论文的实验都是Matlab模拟，效果那叫一个棒。看来问题貌似还是在自己身上 L。

问题二：该算法所获得的波形看似平滑，实则有很多细小的“毛刺”，即自相关算法获得的曲线并不是平滑的，用一些简单的滤波方法像中值滤波，开/闭运算，插值运算中的一种乃至多种一起加诸结果曲线之上，结果仍然有得不到平滑的结果。于是我们就不能用简单的方法判断波峰/波谷的位置了。

问题三：这个问题最为严重，就是算法的C语言实现在上文提到的硬件环境下处理1500个数据（即大约2.5秒的数据量）时需要大约20秒的时间。

至此我们彻底晕菜！！

4 能量+试验经验值之旅

最近研究所新来了几位音频及图像处理的博士，我又满心希望的去请教了一位音频处理方向的博士大哥。获得如下的方法：即认为所获得波形是一种能量的表示，数据值大，代表能量越高，反之，数据值小则代表能量低。能量大的一簇组成了波峰，而能量低的部分则构成了波谷。可以将整个波形分成若干帧，每一帧都代表一小段能量的集合。同时再取出一个阈值T，用于对是否到达波峰进行辅助判断，建议我按下式取阈值T： T=全体数据的均值*a，其中a为一个小于1的实数。这样就可以更好的将杂乱的图形变得比较清晰，从而可以更为容易地判断波形的数量。

受此启发，我实现了一个简单的算法：以20个元素为一帧，将原始波形转化为帧数组，同时顺序扫描该数组，若同时有2帧数据小于阈值T则认为是波峰的起始处，并继续扫描直到有连续两帧小于阈值则认为到达波形的降落处，于是波峰数加一。

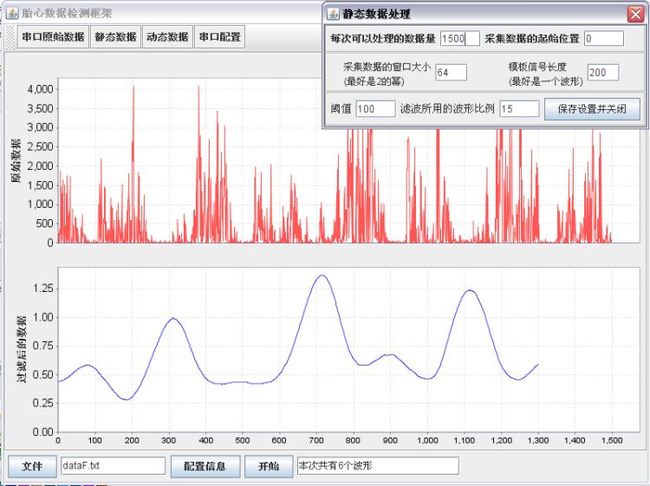
我700个数据的实验结果如下图所示：

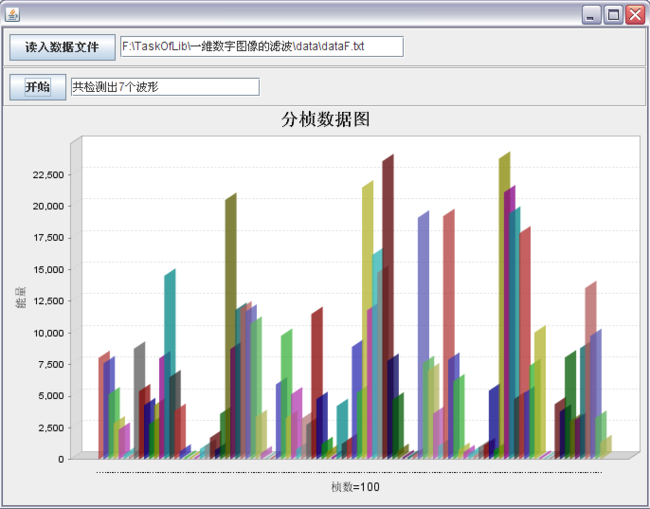
数据量比较多的结果如下所示：

于是我似乎又回到了起点，我还时需要找到一些经验值。首先是选择用于货的阈值T的参数a，到底设成多少才合适？还有就是为什么连续两帧就认为是到达/走出波峰的标志，为什么不能是3帧？所以，目前的结果都是给予我手头有限的数据所能够获得的结果，其中以最后这种勉强还可以用。起码经过大量真实试验的数据锤炼之后，我们应该可以找到不错的参数值，但似乎还是没年能够完全解决问题啊。

5 后记

到目前为止，我的所有算法还是没能够完全脱离某些经验值参数。所以如果哪位朋友能给出一个时间简单的且空间占用率小的算法，请不吝赐教，哪怕是提示也好。如果确实有效的话，作为回报，我会给你发一份我在这次项目中实现的算法的全部工程源码，包括开运算，闭运算，中值滤波，一次/二次插值，快速傅立叶变换，小波变换，平均频率自相关算法的Java或C语言的工程及源码（虽然你不一定用得上 J），同时免费送你一套我们的最终包括硬件和相关软件的产品作为礼物。

本文作者薛笛，目前在黑龙江大学信息技术研究所攻读硕士学位，是一个十足的Java粉丝。可以通过[email protected]与他联系。