uva 1382 - Distant Galaxy
1. 坐标值比较大,所以离散化坐标
2. 坐标的绝对值不超过10^9,说明可能有负数,所以把全部坐标移动转换为正数(加上10^9)
3. mat[i][j] ,表示(0,0) (i, j)为对顶点矩形之内包括边界上有多少个点。
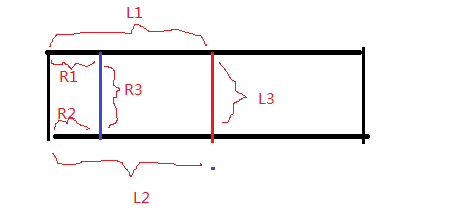
4. 枚举矩形的上下界,然后选择左右边界。 对于确定的左边界left和右边界right, 假设是下图的R3是left, L3是right,那么数量为:
L1 + L2 + L3 - (R1+R2) + R3.
为了要使得以L3为右边界的矩形上的点最多,那么应该使得 R3-(R1+R2)的值最大。
所以,枚举右边界j, 维护保存j左边的R3-(R1+R2)的最大值,只要O(n)就可以确定答案了。
5. 需要注意的是所有点可能都在同一条直线上,所以给横坐标和右坐标都另外添加一个点
代码:
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<iostream>
using namespace std;
const int MAXN = 110;
const int ADD = 1e9+10;
int n;
int arr[MAXN][2];
int mat[MAXN][MAXN];
int X[MAXN], Y[MAXN], row, col;
inline int findID(int* A, int len, int x){
return lower_bound(A, A+len, x)-A+1;
}
inline void input(){
row = 1, col = 1;
X[0] = Y[0] = 0;
for(int i=0; i<n; ++i){
scanf("%d%d", &arr[i][0], &arr[i][1]);
X[row++] = arr[i][0] += ADD;
Y[col++] = arr[i][1] += ADD;
}
sort(X, X+row);
row = unique(X, X+row)-X;
sort(Y, Y+col);
col = unique(Y, Y+col)-Y;
memset(mat, 0, sizeof(mat));
for(int i=0; i<n; ++i){
int a = findID(X, row, arr[i][0]);
int b = findID(Y, col, arr[i][1]);
mat[a][b] = 1;
}
for(int i=1; i<=row; ++i){
for(int j=1; j<=col; ++j)
mat[i][j] += mat[i][j-1]+mat[i-1][j]-mat[i-1][j-1];
}
}
inline int solve(){
int ans = 1;
// 枚举上下界
for(int up=1; up<row; ++up){
for(int down=up+1; down<=row; ++down){
int maxx = mat[down][1]-mat[up-1][1];
for(int i=2; i<=col; ++i){
int right = mat[down][i]-mat[down-1][i]
+ mat[up][i]-mat[up-1][i]
+ mat[down-1][i]-mat[up][i]
- (mat[down-1][i-1]-mat[up][i-1]);
ans = max(ans, right+maxx);
int tmp = mat[down][i]-mat[up-1][i]
- (mat[down][i-1]-mat[up-1][i-1]);
tmp -= mat[down][i]-mat[down-1][i]
+ mat[up][i]-mat[up-1][i];
if(tmp > maxx) maxx=tmp;
}
}
}
return ans;
}
int main(){
int cas=1;
while(~scanf("%d", &n) && n){
input();
printf("Case %d: %d\n", cas++, solve());
}
return 0;
}