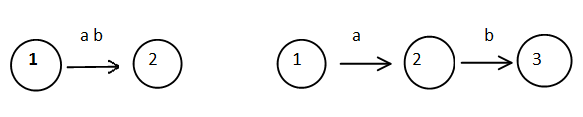形式语言与自动机理论总结
一:图形总结。
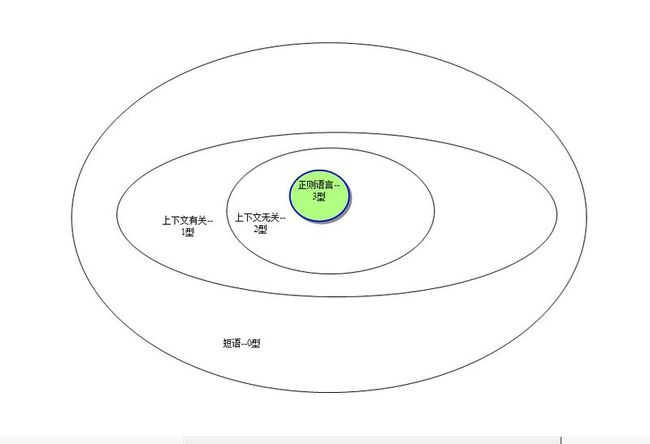
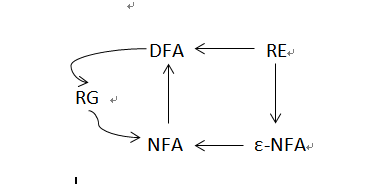
四大文法之间的关系:
总结全图: 点击图片查看大图
二:文字详解。
1,集合关系(并、交、补、差、笛卡尔积、幂积、二元关系)
1) 笛卡尔积:AXB,即都分别对应的乘积。
例1-1,A={1,2,3},B={白、黑}
则 AXB={(1,白),(1,黑),(2,白),(2,黑),(3,白),(3,黑)}
2)幂积:2^A,即所有的子集。
例1-2,A={1,2,3},
则2^A={ Φ,{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}
3)二元关系:任意的R∈A×B,R是A到B的二元关系
2,句子(前后缀)
例2-1,句子abaabb
前缀:ε,a,ab,aba,abaa,abaab,abaabb
真前缀:ε,a,ab,aba,abaa,abaab
后缀:ε,b,bb,abb,aabb,baabb,abaabb
真后缀:ε,b,bb,abb,aabb,baabb
3,文法的构造。
例3-1,L(G):{ a^n b^n|n,m>0}
S->aSb|ab (n,m>=0时,S->aSb|ε )
例3-2,L(G): {a^n b^n a^m b^m|n,m>=0}
S->AB A->aAb|ε B->aBb|ε
4,(1)确定的有穷状态自动机DFA。
特点:1),初态唯一,终态可有多个。
2),任意状态任意射出弧上的元素均不相等
3),识别对象为空时,初态为终态。
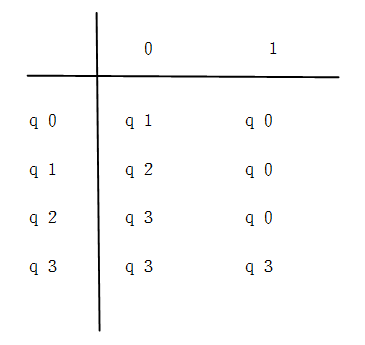
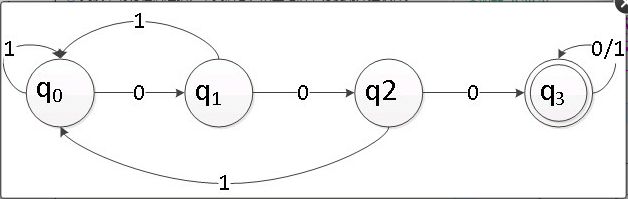
构造:例4-1,L={x000y|x,y ∈{0,1}* }
最小化:
扫描所有的状态对,找出所有的可区分的状态对,不可取分的状态对一定是等价的。
(2)不确定的有穷状态自动机NFA。
特点:1),初态不唯一。
2),同一状态射出弧上的标记可以相同
3),初态可以为终态。
(3)ε-NFA
是在NFA的基础上,允许直接根据当前状态变换到新的状态而不考虑输入带上的符号
(4)等价性
1),NFA与DFA等价、ε-NFA与NFA等价(NFA与DFA等价,ε-NFA与NFA等价,统称它们为FA)
2),FA与正则文法等价(FA和左线性文法、右线性文法等价)
对于一个输入字符,NFA与DFA的差异是前者可以进入若干个状态,而后者只能进入一个惟一的状态。虽然从DFA看待问题的角度来说,NFA在某一时刻同时进入若干个状态,但是,这若干个状态合在一起的“总效果”相当于它处于这些状态对应的一个“综合状态”
5,正则表达式RE-----FA的转换规则
(1)
(2)
(3)
6,正则语言RL
(1)封闭性
1)正则语言的并、交、补是正则语言。
2)正则语言的乘积(连接)是正则语言。
3)正则语言的差是正则语言。
4)正则语言的闭包是正则语言。
5)正则语言的商是正则语言。
6)正则语言的同态是正则语言。
7)正则语言的逆转是正则语言。
附:上下文无关语言CFL的封闭性
1)并、乘积、闭包是封闭的
2)交、补不封闭
(2)泵引理
DFA在处理一个足够长的句子的过程中,必定会重复地经过某一个状态。换句话说,在DFA的状态转移图中,必定存在一条含有回路的从启动状态到某个终止状态的路。由于是回路,所以,DFA可以根据实际需要沿着这个回路循环运行,相当于这个回路中弧上的标记构成的非空子串可以重复任意多次。
(3)等价模型
7,上下文无关语言CFL
(1)语法树
1)每个句型至少存在一颗语法树,每颗语法树至少存在一个推导。
2)每颗树的叶子组成句型(句型就是我们的结果)。
3)每颗简单子树的叶子组成简单短语。
4)最左简单子树的叶子组成句柄。
(2)CFG的化简
1)去无用符号。
首先删除不可终止的,再删除不可到达的
2)去空产生式
先求可空变量,再看空产生式会对哪些产生式有影响
3)去单一产生式
可能会产生新的无用符号或单一产生式
8,图灵机与计算机
(1)用计算机模拟图灵机,不是任何的图灵机都能被计算机来模拟
模拟步骤: 1),在计算机上开辟较大的一维数组来模拟输入带
2),将输入带存入数组
3),转换函数用什么数据结构存储
4),用有穷的编制计算机程序,在输入带上模拟图灵机运行
(2)图灵机比计算机速度慢
(3)运行时间