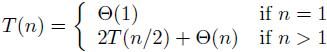算法导论Lecture 1:分析入门
Introduction to Algorithms, MIT OCW 6.046J, Instructors: Prof. Charles Leiserson and Prof. Erik Demaine.
Charles Leiserson (http://people.csail.mit.edu/cel/),即Introduction to Algorithms一书的作者CLRS中的L,1975年获得耶鲁大学计算机学士和数学学士学位,1981年于CMU获得Ph.D学位,其导师为Jon Bentley和H.T.Kung (http://en.wikipedia.org/wiki/Charles_E._Leiserson)。Leiserson教授是麻省理工学院的电气工程和计算机科学教职研究员,麻省理工学院的计算机科学和人工智能实验室(CSAIL)成员,ACM研究员。
Erik Demaine (http://erikdemaine.org/),(b. February 28, 1981, in Halifax, Nova Scotia, Canada),这个加拿大人只比我大四岁,现在是MIT CS系的associate professor。Wiki (http://en.wikipedia.org/wiki/Erik_Demaine)上说他童年的时候跟随他父亲Martin Demaine在北美旅行,他是在家中接受教育的,12岁就进入加拿大的Dalhousie University,并在14岁的时候就完成了他的学士学位。2001年成为MIT faculty,当时他才20岁 (reportedly the youngest professor in the history of the MIT)。史上最年轻的MIT教授,当然称得上是大牛人一个啦!
--Prof. Charles Leiserson
本课程主体分为两个部分,第一部分为算法的分析(Analysis of algorithms),analysis是指:The theoretical study of computer program performance and resource usage,这种分析当然数学性更强一些。 第二部分为算法的设计(Design of algorithms),这是更侧重于工程与应用的一部分。当然在设计有效算法之前需要有基本的分析技巧和方法,这样才能保证算法的效率。
Lecture 1的主题是introduction,由Charles Leiserson教授执教。算法性能的重要性不言而喻。Lecture 1中的第一个程序也是整个课程的第一个程序是排序算法中的插入排序(Insertion sort)。作为性能分析(数学需要准确的定义)的第一个例子,Leiserson教授首先给出了排序的定义:
Output: permutation <a'_1, a'_2, ... , a'_n> such that a'_1 <= a'_2 <= ... <= a'_n
Insertion sort直观易懂,CLRS上用插入扑克牌作为比喻,为了将一堆扑克牌排序,按顺序从扑克牌堆中取牌并将它插入左手中合适的位置即可。
INSERTION-SORT(A, n) // sorts A[1..n], array index starts from 1
for j := 2 to n
do key := A[j]
i := j - 1
while i > 0 and A[i] > key
do A[i+1] := A[i]
i := i - 1
A[i+1] := key
[Ex]. Input: 8 2 4 9 3 6
|__|
2 8 4 9 3 6
|__|
2 4 8 9 3 6
-- no need to swap
2 4 8 9 3 6
|_____|
2 3 4 8 9 6
|____|
2 3 4 6 8 9 -- output
这段程序的运行时间会怎么样呢?首先这是依赖于输入的,比如,输入序列已经是排好序的,或者是反序的,这将产生完全不同的运行时间。另外运行时间还会依赖于输入序列的大小(size of the problem),通常定义为问题的大小。我们希望能够得到运行时间的一个上界,这样对用户(使用这个算法的人)来说会有一个保障,算法运行时间最多不会超过某个界。也就是,
-Depends on input (e.g already sorted, reverse sorted)
-Depends on input size (e.g 6 elements. vs 6*10^9 elements)
-Want upper-bound
-- garantee to the user
那么我们有哪些分析的方法呢?通常我们会把注意力集中在最坏情况(Worst-Case)分析上,即定义给定问题大小n后的运行时间T(n):
有些输入所需时间较短(better),有些则较长(worse),这里的“任何”的意思是,我们只关心那些最长的(最坏的),因为有了这样的最坏时间我们就可以做出保证了。
有时我们会讨论平均情况分析(Average Case)。这里的T(n)为
假定我们知道输入的统计分布,我们可以做平均情况分析。
最不常用的是最好情况分析(Best Case)。Leiserson教授说因为这算是cheat。
同一个问题可以有不同的算法来解决,那么这些算法之间如何比较呢? 通常我们比较它们的相对速度,也就是在同一台机器上比较它们的性能,或者可以不用关心机器,因为我们只关心相对速度。当然我们也可以关注绝对速度,但是绝对速度用的比较少,比如,某个算法可能在任何机器上运行都比较好。在较快的机器上,我的算法运行的当然会快一些,所以这里会产生混淆,在比较算法的快慢的时候我们必须有一个比较的标准或者方式。因此我们就有了算法的BIG IDEA!
THE BIG IDEA
渐近性分析的基本思想是忽略机器相关的常数,关心的是运行时间的增长而不是实际的运行时间。为了能够这样做,我们需要引入一些渐近符号,在这门课程中用的最多的是大theta标记。大theta标记从工程的角度看很简单,对一个公式而言,只需要去掉低阶项,忽略高阶的系数。比如:
[Ex].
![]()
而从数学的角度看,大theta标记有形式的数学定义,这会在Lecture 2中讲到。可以看出当n趋于无穷大的时候,不管那些系数和低阶项是什么,Theta(n^2)的算法总是比Theta(n^3)算法有效,甚至是在一台较慢的机器上也是这样。
当然,在一定的问题大小上,渐近性慢的算法可能仍然是有效的。我们需要在数学理解与工程常识上做出平衡,这样才能编好程序。算法分析并不会自动地让你成为好的程序员。这里Leiserson教授讲到了一个说法:
--Prof. Charles Leiserson
现在来看看Insertion sort的最坏情况分析。最坏情况在输入完全反序的情况下出现,我们要做的就是把所有的操作步骤加起来:
从INSERTION-SORT代码中可以看出,外循环j从2运行到n,内循环中i从j-1运行到1,也就是每一次内循环的运行时间是j-1乘上某个机器相关的常数, 可以用Theta(j)表示。和式是一个算术级数,因此T(n)=Theta(n^2)。
常识告诉我们,对于较小的n,插入排序还是有效的,但是相对较大的n,我们还有更有效的排序算法,比如归并排序(Merge Sort)。为了对一个从1到n的数组排序,归并排序有三个基本步骤:
1. If n = 1, done // T(1)
2. Recursively sort // 2*T(n/2)
A[1 .. ceiling(n/2)] and A[ceiling(n/2)+1 .. n]
3. Merge the 2 sorted list // Theta(n)
第二步是两个递归调用。关键步骤是第三步归并。这里给出归并的一个例子:
[Ex]. 对两列已排好序的数组进行归并操作得到一个排好序的数组:
20 | 12 20 | 12 20 | 12 20 | 12
13 | 11 13 | 11 13 | 11 (13) | 11
7 | 9 7 | (9) (7) | (9) (7) | (9)
(2) | (1) => (2) | (1) => (2) | (1) => (2) | (1) => ...
Output 1 1, 2 1,2,7 1,2,7,9
归并的每一步都是与数组大小无关的常数,所以对n个元素的归并所需的时间是Theta(n)。
由以上的分析可以得到归并排序的运行时间T(n),这是一个递归表达式:
对于这样的递归式,通常有三种方法来处理(Lecture 2中会讲到解递归的方法)。这里Leiserson教授给出用递归树(Recursion Tree)的方法来解这个式子。
当n=1时T(1)是个常数,对这样的平凡的情况我们可以不用关心,我们只对n>1的情况感兴趣。也就是T(n)=2T(n/2)+Theta(n)。并且我们会把式子中的Theta(n)去掉,用一个系数大于零的线性函数取代,比如cn,(c>0)。Lecture 2中会讲到这些渐近性标记的处理方式。也就是T(n)=2T(n/2)+cn, (c>0)。我们可以把这个式子表示成树状的形式:
T(n) = cn = cn = cn cn
/ \ / \ / \
T(n/2) T(n/2) / \ cn/2 cn/2 2*cn/2 = cn
cn/2 cn/2 / \ / \
/ \ / \ cn/4 ... 4*cn/4 = cn
/ \ / \ . .
T(n/4) . . . . .
. .
T(1) ... + n*T(1) // 把所有项加起来
--------------
cn lg n + Theta(n)
(这里用了很多.来表示省略没有写出的部分。)假定这个树的高度为h,则有2^h=n,因些h=lg n,也就是有lg n个cn,再加上n*T(1),T(1)=Theta(1),即Theta(n)。因些我们可以得出T(n) = Theta(nlg n)。
所以当n足够大的时候,归并排序总是比插入排序更有效的。
第一课至此也就完成了。我们看到了分析的定义,要处理什么样的问题以及不同的分析方法。以排序为例,给出了运行时间的概念。要分析相对的运行速度,我们引入了渐近性分析的概念,从工程与数学的角度来看渐近性分析的内容以及这样的分析能给我们带来什么。比较插入排序与归并排序的渐近运行时间,当n问题规模足够大时归并排序总是比插入排序要有效。Leiserson教授还给出了用递归树来解递归的方法。