Java_NetWork_Endianness-字节序

网络编程一般会使用字节序方面的知识，这里做个入门吧。

Endianness-字节序

维基百科：http://zh.wikipedia.org/wiki/%E5%AD%97%E8%8A%82%E5%BA%8F

字节序，又称端序，尾序，英文：Endianness。在计算机科学领域中，字节序是指存放多字节数据的字节（byte）的顺序，典型的情况是整数在内存中的存放方式和网络传输的传输顺序。Endianness有时候也可以用指位序（bit）。

一般而言，字节序指示了一个UCS-2字符的哪个字节存储在低地址。如果LSByte在MSByte的前面，即LSB为低地址，则该字节序是小端序；反之则是大端序。在网络编程中，字节序是一个必须被考虑的因素，因为不同的处理器体系可能采用不同的字节序。在多平台的代码编程中，字节序可能会导致难以察觉的bug。

endian词源

“endian”一词来源于乔纳森·斯威夫特的小说格列佛游记。小说中，小人国为水煮蛋该从大的一端（Big-End）剥开还是小的一端（Little-End）剥开而争论，争论的双方分别被称为Big-endians和Little-endians。

1980年，DannyCohen在其著名的论文"OnHoly Wars and a Plea for Peace"中，为平息一场关于字节该以什么样的顺序传送的争论，而引用了该词。

基本的字节序

对于单一的字节（abyte），大部分处理器以相同的顺序处理位元（bit），因此单字节的存放方法和传输方式一般相同。

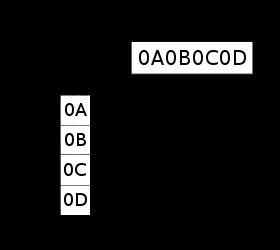
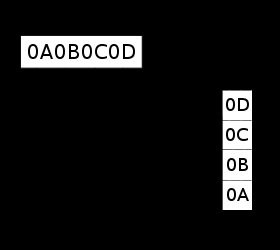
对于多字节数据，如整数（32位机中一般占4字节），在不同的处理器的存放方式主要有两种，以内存中0x0A0B0C0D的存放方式为例，分别有以下几种方式：

注 : 0x 前缀代表十六进制。

大端序

大端序（英：big-endian）或稱大尾序。

• 数据以8bit为单位:

地址增长方向→
...	0x0A	0x0B	0x0C	0x0D	...

示例中，最高有效位（MSB,Most SignificantByte）是0x0A存储在最低的内存地址处。下一个字节0x0B存在后面的地址处。正类似于十六进制字节从左到右的阅读顺序。

• 数据以16bit为单位:

地址增长方向→
...	0x0A0B	0x0C0D	...

最高的16bit单元0x0A0B存储在低位。

小端序

小端序（英：little-endian）或稱小尾序。

• 数据以8bit为单位:

地址增长方向→
...	0x0D	0x0C	0x0B	0x0A	...

最低有效位（LSB,LeastSignificant Byte）是0x0D存储在最低的内存地址处。后面字节依次存在后面的地址处。

• 数据以16bit为单位:

地址增长方向→
...	0x0C0D	0x0A0B	...

最低的16bit单元0x0C0D存储在低位。

• 更改地址的增长方向:

当更改地址的增长方向，使之由右至左时，表格更具有可阅读性。

←地址增长方向
...	0x0A	0x0B	0x0C	0x0D	...

最低有效位（LSB）是0x0D存储在最低的内存地址处。后面字节依次存在后面的地址处。

←地址增长方向
...	0x0A0B	0x0C0D	...

最低的16bit单元0x0C0D存储在低位。

混合序

混合序（英：middle-endian）具有更复杂的顺序。以PDP-11为例，0x0A0B0C0D被存储为：

• 32bit在PDP-11的存储方式

地址增长方向→
...	0x0B	0x0A	0x0D	0x0C	...

可以看作最高的16bit位和低位以大端序存储，但16bit内部以小端存储。

处理器体系

• x86，MOSTechnology 6502，Z80，VAX，PDP-11等处理器为Littleendian。

• Motorola6800，Motorola68000，PowerPC970，System/370，SPARC（除V9外）等处理器为Bigendian

• ARM,PowerPC(除PowerPC970外),DECAlpha,SPARCV9,MIPS,PA-RISCandIA64的字节序是可配置的。

网络序

网络传输一般采用大端序，也被称之为网络字节序，或网络序。IP协议中定义大端序为网络字节序。

伯克利socketAPI定义了一组转换函数，用于16和32bit整数在网络序和本机字节序之间的转换。htonl，htons用于本机序转换到网络序；ntohl，ntohs用于网络序转换到本机序。

位序

一般用于描述串行设备的传输顺序。一般硬件传输采用小端序（先传低位），但I2C协议采用大端序。网络协议中只有数据链路层的底端会涉及到。

Big and Little Endian

来自：http://www.cs.umd.edu/class/sum2003/cmsc311/Notes/Data/endian.html

Basic Memory Concepts

In order to understand the concept of big and little endian, you need to understand memory. Fortunately, we only need a very high level abstraction for memory. You don't need to know all the little details of how memory works.

All you need to know about memory is that it's one large array. But one large array containing what? The array containsbytes. In computer organization, people don't use the term "index" to refer to the array locations. Instead, we use the term "address". "address" and "index" mean the same, so if you're getting confused, just think of "address" as "index".

Each address stores one element of the memory "array". Each element is typically one byte. There are some memory configurations where each address stores something besides a byte. For example, you might store a nybble or a bit. However, those are exceedingly rare, so for now, we make the broad assumption that all memory addresses store bytes.

I will sometimes say that memory isbyte-addresseable. This is just a fancy way of saying that each address stores one byte. If I say memory isnybble-addressable, that means each memory address stores one nybble.

Storing Words in Memory

We've defined a word to mean 32 bits. This is the same as 4 bytes. Integers, single-precision floating point numbers, and MIPS instructions are all 32 bits long. How can we store these values into memory? After all, each memory address can store a single byte, not 4 bytes.

The answer is simple. We split the 32 bit quantity into 4 bytes. For example, suppose we have a 32 bit quantity, written as 90AB12CD16, which is hexadecimal. Since each hex digit is 4 bits, we need 8 hex digits to represent the 32 bit value.

So, the 4 bytes are: 90, AB, 12, CD where each byte requires 2 hex digits.

It turns out there are two ways to store this in memory.

Big Endian

In big endian, you store the most significant byte in the smallest address. Here's how it would look:

Address	Value
1000	90
1001	AB
1002	12
1003	CD

Little Endian

In little endian, you store theleastsignificant byte in the smallest address. Here's how it would look:

Address	Value
1000	CD
1001	12
1002	AB
1003	90

Notice that this is in the reverse order compared to big endian. To remember which is which, recall whether the least significant byte is stored first (thus, little endian) or the most significant byte is stored first (thus, big endian).

Notice I used "byte" instead of "bit" in least significant bit. I sometimes abbreciated this as LSB and MSB, with the 'B' capitalized to refer to byte and use the lowercase 'b' to represent bit. I only refer to most and least significant byte when it comes to endianness.

Which Way Makes Sense?

Different ISAs use different endianness. While one way may seem more natural to you (most people think big-endian is more natural), there is justification for either one.

For example, DEC and IBMs(?) are little endian, while Motorolas and Suns are big endian. MIPS processors allowed you to select a configuration where it would be big or little endian.

Why is endianness so important? Suppose you are storing int values to a file, then you send the file to a machine which uses the opposite endianness and read in the value. You'll run into problems because of endianness. You'll read in reversed values that won't make sense.

Endianness is also a big issue when sending numbers over the network. Again, if you send a value from a machine of one endianness to a machine of the opposite endianness, you'll have problems. This is even worse over the network, because you might not be able to determine the endianness of the machine that sent you the data.

The solution is to send 4 byte quantities usingnetwork byte orderwhich is arbitrarily picked to be one of the endianness (not sure if it's big or little, but it's one of them). If your machine has the same endianness as network byte order, then great, no change is needed. If not, then you must reverse the bytes.

History of Endian-ness

Where does this term "endian" come from? Jonathan Swift was a satirist (he poked fun at society through his writings). His most famous book is "Gulliver's Travels", and he talks about how certain people prefer to eat their hard boiled eggs from the little end first (thus, little endian), while others prefer to eat from the big end (thus, big endians) and how this lead to various wars.

Of course, the point was to say that it was a silly thing to debate over, and yet, people argue over such trivialities all the time (for example, should braces line in parallel or not? vi or emacs? UNIX or Windows).

Misconceptions

Endianness only makes sense when you want to break a large value (such as a word) into several small ones. You must decide on an order to place it in memory.

However, if you have a 32 bit register storing a 32 bit value, it makes no sense to talk about endianness. The register isneitherbig endiannorlittle endian. It's just a register holding a 32 bit value. The rightmost bit is the least significant bit, and the leftmost bit is the most significant bit.

There's no reason to rearrange the bytes in a register in some other way.

Endianness only makes sense when you are breaking up a multi-byte quantity, and attempting to store the bytes at consecutive memory locations. In a register, it doesn't make sense. A register is simply a 32 bit quantity,b₃₁....b₀, and endianness does not apply to it.

With regard to endianness, You may argue there's a very natural way to store 4 bytes in 4 consecutive addresses, and that the other way looks strange. In particular, it looks "backwards". However, what's natural to you may not be natural to someone else. The fact of the matter is that the word is split in 4 bytes, and most people would agree that you needsomeorder to place it in memory.

C-style strings

Once you start thinking about endianness, you begin to think it applies to everything. Before you see big or little endian, you may have had no idea it even existed. That's because it's reasonably well-hidden from you.

If you do bitwise/bitshift operations on an int, you don't notice the endianness. The machine arranges the multiple bytes so the least significant byte is still the least significant byte (e.g.,b_7-0) and the most significant byte is still the most significant byte (e.g.,b_31-24).

So, it's natural to think whether strings might be saved in some sort of strange order, depending on the machine.

This is where it's useful to think about all the facts you know about arrays. A C-style string, after all, is still an array of characters.

Here are some facts you should know about C-style strings and arrays.

• C-style strings are stored in arrays of characters.
• Each character requires one byte of memory, since characters are represented in ASCII (in the future, this could change, as Unicode becomes more popular).
• In an array, the address of consecutive array elements increases. Thus,& arr[ i ]is less than& arr[ i + 1 ].
• What's not as obvious is that if something is stored in increasing addresses in memory, it's going to be stored in increasing "addresses" in a file. When you write to a file, you usually specify an address in memory, and the number of bytes you wish to write to the file starting at that address.

So, let's imagine some C-style string in memory. You have the word "cat". Let's pretend 'c' is stored at address 1000. Then 'a' is stored at 1001. 't' is at 1002. The null character '/0' is at 1003.

Since C-style strings are arrays of characters, they follow the rules of characters. Unlike int or long, you can easily see the individual bytes of a C-style string, one byte at a time. You use array indexing to access the bytes (i.e., characters) of a string. You can't easily index the bytes of an int or long, without playing some pointer tricks (using reinterpret cast, for example, in C++). The individual bytes of an int are more or less hidden from you.

Now imagine writing out this string to a file using some sort ofwrite()method. You specify a pointer to 'c', and the number of bytes you wish to print (in this case 4). Thewrite()method proceeds byte by byte in the character string and writes it to the file, starting with 'c' and working to the null character.

Given that explanation, is it clear whether endianness matters with C-style strings? Hopefully, it is clear.

As an aside, since C++ strings are objects, it may have complicated inner structures, and so it's less obvious what a C++ string would look like when print out to a file. It's well-known what a C-style string looks like (a sequence of characters ending in a null character), which is why I've been careful to call them C-style strings.

Endianness一点通

来自：http://packetmania.bokee.com/511210.html

Endianness 的问题实质就是关于计算机如何存储大的数值的问题。

我们知道一个基本存储单元可以保存一个字节，每个存储单元对应一个地址。对于大于十进制255（16进制0xff）的整数，需要多个存储单元。例如，4660对应于0x1234，需要两个字节。不同的计算机系统使用不同的方法保存这两个字节。在我们常用的PC机中，低位的字节0x34保存在低地址的存储单元，高位的字节0x12保存在高地址的存储单元；而在Sun工作站中，情况恰恰相反，0x34位于高地址的存储单元，0x12位于低地址的存储单元。前一种就被称为Little Endian，后一种就是Big Endian。

如何记住这两种存储模式？其实很简单。首先记住我们所说的存储单元的地址总是由低到高排列。对于多字节的数值，如果先见到的是低位的字节，则系统就是Little Endian的，Little 就是"小，少"的意思，也就对应"低"。相反就是Big Endian，这里 Big "大"对应"高"。

为了加深对Endianness的理解，让我们来看下面的C程序例子：

char a = 1;
charb = 2;		地址偏移量	内存映像
short c = 255;	/* 0x00ff */	0x0000:	0102FF00
longd = 0x44332211;		0x0004:	11 22 33 44

在右侧我们可以见到在基于Intel 80x86的系统上的内存映像，显然我们可以马上判定这一系统是Little Endian的。对于16位的整形数(short)c，我们先见到其低位的0xff，下一个才是0x00。同样对于32位长整形数(long)d，在最低的地址0x0004存的是最低位字节0x11。如果是在Big Endian的计算机中，则地址偏移量从0x0000到0x0007的整个内存映像将为：01 02 00 FF 44 33 22 11。

所有计算机处理器都必须在这两种Endian间作出选择。但某些处理器(如MIPS和IA-64)支持两种模式，可由编程者通过软件或硬件设置一种Endian。以下是一个处理器类型与对应的Endian的简表：

纯Big Endian: SunSPARC,Motorola 68000，Java Virtual Machine

Bi-Endian,运行Big Endian模式:MIPS运行IRIX,PA-RISC，大多数Power和PowerPC系统

Bi-Endian, 运行Little Endian模式:MIPS 运行Ultrix，大多数DECAlpha,IA-64运行Linux

Little Endian:Intel x86，AMD64，DECVAX

如何在程序中检测本系统的Endianess？可调用下面的函数来快速验证，如果返回值为1，则为Little Endian；为0则是Big Endian：

int testendian() {
int x = 1;
return *((char *)&x);
}

Endianness对于网络通信也很重要。试想当Little Endian系统与Big Endian的系统通信时，如果不做适当处理，接收方与发送方对数据的解释将完全不一样。比如对以上C程序段中的变量d，Little Endian发送方发出11 22 33 44四个字节，Big Endian接收方将其转换为数值0x11223344。这与原始的数值大相径庭。为了解决这个问题，TCP/IP协议规定了专门的"网络字节次序"，即无论计算机系统支持何种Endian，在传输数据时，总是数值最高位的字节最先发送。从定义可以看出，网络字节次序其实是对应Big Endian的。

为了避免因为Endianness造成的通信问题，及便于软件开发者编写易于平台移植的程序，特别定义了一些C语言预处理的宏来实现网络字节与主机字节次序之间的相互转换。htons()和htonl()用来将主机字节次序转成网络字节次序，前者应用于16位无符号数，后者应用于32位无符号数。ntohs()和ntohl()实现反方向的转换。这四个宏的原型定义可参考如下(Linux系统中可在netinet/in.h文件里找到)：

#if defined(BIG_ENDIAN) && !defined(LITTLE_ENDIAN)

#define htons(A)  (A)
#define htonl(A)  (A)
#define ntohs(A)  (A)
#define ntohl(A)  (A)

#elif defined(LITTLE_ENDIAN) && !defined(BIG_ENDIAN)

#define htons(A)  ((((uint16)(A) & 0xff00) >> 8) | /
                   (((uint16)(A) & 0x00ff) << 8))
#define htonl(A)  ((((uint32)(A) & 0xff000000) >> 24) | /
                   (((uint32)(A) & 0x00ff0000) >> 8)  | /
                   (((uint32)(A) & 0x0000ff00) << 8)  | /
                   (((uint32)(A) & 0x000000ff) << 24))
#define ntohs     htons
#define ntohl     htohl

#else

#error "Either BIG_ENDIAN or LITTLE_ENDIAN must be #defined, but not both."

#endif

综上所说，可以总结几点：

1. 小端法(Little-Endian)

就是低位字节排放在内存的低地址端即该值的起始地址，高位字节排放在内存的高地址端。

2. 大端法(Big-Endian)

就是高位字节排放在内存的低地址端即该值的起始地址，低位字节排放在内存的高地址端。

如：

3. 不同的平台存储数据的顺序不一样。

4. TCP/IP 协议规定网络字节序是Big-Endian

网络字节顺序是TCP/IP中规定好的一种数据表示格式，它与具体的CPU类型、操作系统等无关，从而可以保证数据在不同主机之间传输时能够被正确解释。网络字节顺序采用big endian排序方式。
网络字节序定义：收到的第一个字节被当作高位看待，这就要求发送端发送的第一个字节应当是高位。而在发送端发送数据时，发送的第一个字节是该数字在内存中起始地址对应的字节。可见多字节数值在发送前，在内存中数值应该以大端法存放（因为Big-endian最高有效位在低内存地址，传输时先传低内存对应的字节即最高有效位）。
网络字节序说是大端字节序。

5.在网络程序开发时或是跨平台开发时，也应该注意保证只用一种字节序，不然两方的解释不一样就会产生bug.

6. 判断cpu的字节序

#include <stdio.h> int main() { union ut { short s; char c[2]; }u; if(sizeof(short) == 2) { u.s = 0x0102; if(u.c[0] == 1 && u.c[1] == 2) { printf("big enidan/n"); } else if (u.c[0] == 2 && u.c[1] == 1) { printf("little endian./n"); } return 0; } }