HDUOJ1874 畅通工程续 和 NYOJ 115 城市平乱【Dijkstra 算法】
原题链接:nyoj 115:http://acm.nyist.net/JudgeOnline/problem.php?pid=115 hduoj 1874:http://acm.hdu.edu.cn/showproblem.php?pid=1874
一、Dijkstra 算法的介绍
Dijkstra 算法,又叫迪科斯彻算法(Dijkstra),
算法解决的是有向图中单个源点到其他顶点的最短路径问题。
举例来说,
如果图中的顶点表示城市,而边上的权重表示著城市间开车行经的距离,
Dijkstra 算法可以用来找到两个城市之间的最短路径。
二、Dijkstra 的算法实现
Dijkstra 算法的输入包含了一个有权重的有向图 G,以及G中的一个来源顶点 S。
我们以 V 表示 G 中所有顶点的集合,以 E 表示G 中所有边的集合。
(u, v) 表示从顶点 u 到 v 有路径相连,而边的权重则由权重函数 w: E → [0, ∞] 定义。
因此,w(u, v) 就是从顶点 u 到顶点 v 的非负花费值(cost),边的花费可以想像成两个顶点之间的距离。
任两点间路径的花费值,就是该路径上所有边的花费值总和。
已知有 V 中有顶点 s 及 t,Dijkstra 算法可以找到 s 到 t 的最低花费路径(例如,最短路径)。
这个算法也可以在一个图中,找到从一个顶点 s 到任何其他顶点的最短路径。
三、图文解析Dijkstra 算法
ok,经过上文有点繁杂的信息,你还并不对此算法了如指掌,清晰透彻。
没关系,咱们来幅图,就好了。请允许我再对此算法的概念阐述下,
Dijkstra算法是典型最短路径算法,用于计算一个节点到其他所有节点的最短路径。
不过,针对的是非负值权边。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
[Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。]
ok,请看下图:
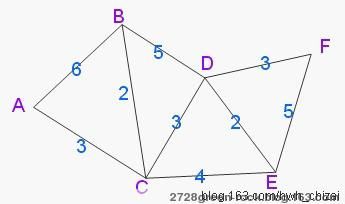
如下图,设A为源点,求A到其他各所有一一顶点(B、C、D、E、F)的最短路径。线上所标注为相邻线段之间的距离,即权值。
(注:此图为随意所画,其相邻顶点间的距离与图中的目视长度不能一一对等)
Dijkstra无向图
算法执行步骤如下表:
是不是对此Dijkstra 算法有不错的了解了。。。讲解就到这里了。。
讲解参考:http://blog.csdn.net/v_JULY_v/article/details/6096981
现在说说oj这两个题:
nyoj 115: 懂了dijkstra 后该题没啥难度了,以城市为 起点 执行一次 求他到各个城市的最短距离,再找出有部队的城市,找到一个最小路 输出即可。。
代码:
HDUOJ 1874:
这个题 有点那个什么。。卡了我很久呀!!!还是题意没搞透彻。。⊙﹏⊙。。先用并查集 来判断 题中的S T,是否可以连通。不会并查集的可看我另一篇讲并查集的博客,自己找一下。若不连通,后面就不用执行了,直接下一次循环。。还有个让人蛋疼的条件就是两个城市之间 可能不止一条路!!就是在赋值时加上一个 i f 判断。。
代码: